Article contents
The importance of bubble deformability for strong drag reduction in bubbly turbulent Taylor–Couette flow
Published online by Cambridge University Press: 28 March 2013
Abstract
Bubbly turbulent Taylor–Couette (TC) flow is globally and locally studied at Reynolds numbers of 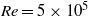 $\mathit{Re}= 5\times 1{0}^{5} $ to
$\mathit{Re}= 5\times 1{0}^{5} $ to 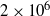 $2\times 1{0}^{6} $ with a stationary outer cylinder and a mean bubble diameter around 1 mm. We measure the drag reduction (DR) based on the global dimensional torque as a function of the global gas volume fraction
$2\times 1{0}^{6} $ with a stationary outer cylinder and a mean bubble diameter around 1 mm. We measure the drag reduction (DR) based on the global dimensional torque as a function of the global gas volume fraction 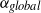 ${\alpha }_{global} $ over the range 0–4 %. We observe a moderate DR of up to 7 % for
${\alpha }_{global} $ over the range 0–4 %. We observe a moderate DR of up to 7 % for 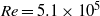 $\mathit{Re}= 5. 1\times 1{0}^{5} $. Significantly stronger DR is achieved for
$\mathit{Re}= 5. 1\times 1{0}^{5} $. Significantly stronger DR is achieved for 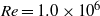 $\mathit{Re}= 1. 0\times 1{0}^{6} $ and
$\mathit{Re}= 1. 0\times 1{0}^{6} $ and 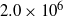 $2. 0\times 1{0}^{6} $ with, remarkably, more than
$2. 0\times 1{0}^{6} $ with, remarkably, more than 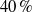 $40\hspace{0.167em} \% $ of DR at
$40\hspace{0.167em} \% $ of DR at 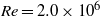 $\mathit{Re}= 2. 0\times 1{0}^{6} $ and
$\mathit{Re}= 2. 0\times 1{0}^{6} $ and 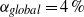 ${\alpha }_{global} = 4\hspace{0.167em} \% $. To shed light on the two apparently different regimes of moderate DR and strong DR, we investigate the local liquid flow velocity and the local bubble statistics, in particular the radial gas concentration profiles and the bubble size distribution, for the two different cases:
${\alpha }_{global} = 4\hspace{0.167em} \% $. To shed light on the two apparently different regimes of moderate DR and strong DR, we investigate the local liquid flow velocity and the local bubble statistics, in particular the radial gas concentration profiles and the bubble size distribution, for the two different cases: 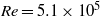 $\mathit{Re}= 5. 1\times 1{0}^{5} $ in the moderate DR regime and
$\mathit{Re}= 5. 1\times 1{0}^{5} $ in the moderate DR regime and 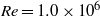 $\mathit{Re}= 1. 0\times 1{0}^{6} $ in the strong DR regime, both at
$\mathit{Re}= 1. 0\times 1{0}^{6} $ in the strong DR regime, both at 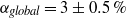 ${\alpha }_{global} = 3\pm 0. 5\hspace{0.167em} \% $. In both cases the bubbles mostly accumulate close to the inner cylinder (IC). Surprisingly, the maximum local gas concentration near the IC for
${\alpha }_{global} = 3\pm 0. 5\hspace{0.167em} \% $. In both cases the bubbles mostly accumulate close to the inner cylinder (IC). Surprisingly, the maximum local gas concentration near the IC for 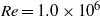 $\mathit{Re}= 1. 0\times 1{0}^{6} $ is
$\mathit{Re}= 1. 0\times 1{0}^{6} $ is 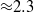 ${\approx }2. 3$ times lower than that for
${\approx }2. 3$ times lower than that for 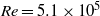 $\mathit{Re}= 5. 1\times 1{0}^{5} $, in spite of the stronger DR. Evidently, a higher local gas concentration near the inner wall does not guarantee a larger DR. By defining and measuring a local bubble Weber number (
$\mathit{Re}= 5. 1\times 1{0}^{5} $, in spite of the stronger DR. Evidently, a higher local gas concentration near the inner wall does not guarantee a larger DR. By defining and measuring a local bubble Weber number (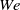 $\mathit{We}$) in the TC gap close to the IC wall, we observe that the cross-over from the moderate to the strong DR regime occurs roughly at the cross-over of
$\mathit{We}$) in the TC gap close to the IC wall, we observe that the cross-over from the moderate to the strong DR regime occurs roughly at the cross-over of 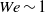 $\mathit{We}\sim 1$. In the strong DR regime at
$\mathit{We}\sim 1$. In the strong DR regime at 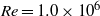 $\mathit{Re}= 1. 0\times 1{0}^{6} $ we find
$\mathit{Re}= 1. 0\times 1{0}^{6} $ we find 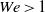 $\mathit{We}\gt 1$, reaching a value of
$\mathit{We}\gt 1$, reaching a value of 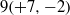 $9(+ 7, - 2)$ when approaching the inner wall, indicating that the bubbles increasingly deform as they draw near the inner wall. In the moderate DR regime at
$9(+ 7, - 2)$ when approaching the inner wall, indicating that the bubbles increasingly deform as they draw near the inner wall. In the moderate DR regime at 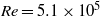 $\mathit{Re}= 5. 1\times 1{0}^{5} $ we find
$\mathit{Re}= 5. 1\times 1{0}^{5} $ we find 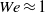 $\mathit{We}\approx 1$, indicating more rigid bubbles, even though the mean bubble diameter is larger, namely
$\mathit{We}\approx 1$, indicating more rigid bubbles, even though the mean bubble diameter is larger, namely 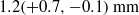 $1. 2(+ 0. 7, - 0. 1)~\mathrm{mm} $, as compared with the
$1. 2(+ 0. 7, - 0. 1)~\mathrm{mm} $, as compared with the 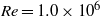 $\mathit{Re}= 1. 0\times 1{0}^{6} $ case, where it is
$\mathit{Re}= 1. 0\times 1{0}^{6} $ case, where it is 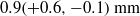 $0. 9(+ 0. 6, - 0. 1)~\mathrm{mm} $. We conclude that bubble deformability is a relevant mechanism behind the observed strong DR. These local results match and extend the conclusions from the global flow experiments as found by van den Berg et al. (Phys. Rev. Lett., vol. 94, 2005, p. 044501) and from the numerical simulations by Lu, Fernandez & Tryggvason (Phys. Fluids, vol. 17, 2005, p. 95102).
$0. 9(+ 0. 6, - 0. 1)~\mathrm{mm} $. We conclude that bubble deformability is a relevant mechanism behind the observed strong DR. These local results match and extend the conclusions from the global flow experiments as found by van den Berg et al. (Phys. Rev. Lett., vol. 94, 2005, p. 044501) and from the numerical simulations by Lu, Fernandez & Tryggvason (Phys. Fluids, vol. 17, 2005, p. 95102).
JFM classification
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
Footnotes
Present address: Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany.
References
- 83
- Cited by


