Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-30T22:56:03.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Impinging planar jet flow on a horizontal surface with slip

Published online by Cambridge University Press:  28 October 2016

Roger E. Khayat
Roger E. Khayat*
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, Ontario, Canada N6A 5B9
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow of a planar jet (sheet) impinging onto a solid flat plate with slip is examined theoretically. The jet is assumed to spread out in a thin layer bounded by a hydraulic jump, and draining at the edge of the plate. In contrast to an adhering jet, a slipping jet does not admit a similarity solution. Taking advantage of the different scaling in each region, series expansions are used in the developing and fully viscous layers, which are matched at the transition point. We show that a slipping film exhibits a singularity in the normal stress at the leading edge of the boundary layer, as opposed to the singularity in velocity and shear stress for an adhering film. The boundary-layer and film heights are both found to decrease with slip relative to a smooth substrate, roughly like 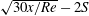$\sqrt{30x/Re}-2S$, whereas the slip velocity intensifies like 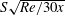$S\sqrt{Re/30x}$ with slip. Here, $x$ is the distance along the plate, 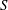$S$ is the slip length and 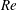$Re$ is the Reynolds number (in units of the jet width). The transition is delayed by slip. Guided by the measurements of Duchesne et al. (Europhys. Lett., vol. 107, 2014, p. 54002) for a circular adhering jet, the hydraulic-jump height and location are determined for a planar jet, and are found to increase with the Froude number (flow rate) like 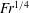$Fr^{1/4}$ and 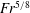$Fr^{5/8}$ respectively, essentially independently of slip length.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Mathematical Foundations: Mathematical Foundations Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 808 , 10 December 2016 , pp. 258 - 289
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajadi, S. O., Adegoke, A. & Aziz, A. 2009 Slip boundary layer flow of non-Newtonian fluid over a flat plate with convective thermal boundary condition. Intl J. Nonlinear Sci. 8, 300.Google Scholar
Baonga, J. B., Louahlia-Gualous, H. & Imbert, M. 2006 Experimental study of the hydrodynamic and heat transfer of free liquid jet impinging a flat circular heated disk. Appl. Therm. Engng 26, 1125.Google Scholar
Benilov, E. S. 2015 Hydraulic jumps in a shallow flow down a slightly inclined substrate. J. Fluid Mech. 782, 5.Google Scholar
Bohr, T., Dimon, P. & Putzkaradze, V. 1993 Shallow-water approach to the circular hydraulic jump. J. Fluid Mech. 254, 635.CrossRefGoogle Scholar
Bowles, R. I. & Smith, F. T. 1992 The standing hydraulic jump: theory, computations and comparisons with experiments. J. Fluid Mech. 242, 145.Google Scholar
Bush, J. W. M. & Aristoff, J. M. 2003 The influence of surface tension on the circular hydraulic jump. J. Fluid Mech. 489, 229.Google Scholar
Craik, A., Latham, R., Fawkes, M. & Gibbon, P. 1981 The circular hydraulic jump. J. Fluid Mech. 112, 347.Google Scholar
Dressaire, E., Courbin, L., Crest, J. & Stone, H. A. 2009 Thin-film fluid flows over microdecorated surfaces: observation of polygonal hydraulic jumps. Phys. Rev. Lett. 102, 194193.Google Scholar
Dressaire, E., Courbin, L., Crest, J. & Stone, H. A. 2010 Inertia dominated thin-film flows over microdecorated surfaces. Phys. Fluids 22, 073602.Google Scholar
Duchesne, A., Lebon, L. & Limat, L. 2014 Constant Froude number in a circular hydraulic jump and its implication on the jump radius selection. Europhys. Lett. 107, 54002.Google Scholar
Goren, S. L. & Wronski, S. 1966 The shape of low-speed capillary jets of Newtonian liquids. J. Fluid Mech. 25, 185.Google Scholar
Khayat, R. E. 2014 Free-surface jet flow of a shear-thinning power-law fluid near the channel exit. J. Fluid Mech. 748, 580.Google Scholar
Khayat, R. E. 2016 Slipping free jet flow near channel exit at moderate Reynolds number for large slip length. J. Fluid Mech. 793, 667.Google Scholar
Khayat, R. E. & Kim, K. 2006 Thin-film flow of a viscoelastic fluid on an axisymmetric substrate of arbitrary shape. J. Fluid Mech. 552, 37.Google Scholar
Laurmann, J. A. 1961 Linearized slip flow past a semi-infinite flat plate. J. Fluid Mech. 11, 82.Google Scholar
Liu, X., Gabour, L. A. & Lienhard, J. 1993 Stagnation-point heat transfer during impingement of laminar liquid jets: analysis including surface tension. Trans. ASME J. Heat Transfer 115, 99.Google Scholar
Liu, X. & Lienhard, J. 1993 The hydraulic jump in circular jet impingement and in other thin liquid films. Exp. Fluids 15, 108.Google Scholar
Martin, M. J. & Boyd, l. D. 2001 Blasius boundary layer solution with slip flow conditions. In Rarefied Gas Dynamics: 22nd International Symposium (ed. Bartel, T. J. & Gallis, M. A.), p. 518.Google Scholar
Mitchell, S. L. & Myers, T. G. 2010 Application of standard and refined heat balance integral methods to one-dimensional Stefan problems. SIAM Rev. 52, 57.CrossRefGoogle Scholar
Murray, J. D. 1965 Incompressible slip flow past a semi-infinite flat plate. J. Fluid Mech. 22, 463.Google Scholar
Ou, J. & Rothstein, J. P. 2005 Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys. Fluids 17, 103606.Google Scholar
Prince, J. F., Maynes, D. & Crockett, J. 2012 Analysis of laminar jet impingement and hydraulic jump on a horizontal surface with slip. Phys. Fluids 24, 102103.Google Scholar
Rojas, N., Argentina, M. & Tirapegui, E. 2013 A progressive correction to the circular hydraulic jump scaling. Phys. Fluids 25, 042105.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89.Google Scholar
Schlichting, H. 2000 Boundary-layer Theory, 8th edn. Springer.CrossRefGoogle Scholar
Stevens, J. & Webb, B. W. 1992 Measurements of the free surface flow structure under an impinging, free liquid jet. Trans. ASME J. Heat Transfer 114, 79–84.Google Scholar
Watson, E. 1964 The spread of a liquid jet over a horizontal plane. J. Fluid Mech. 20, 481–499.Google Scholar
White, F. M. 2015 Fluid Mechanics, 8th edn. McGraw-Hill.Google Scholar
Zhao, J. & Khayat, R. E. 2008 Spread of a non-Newtonian liquid jet over a horizontal plate. J. Fluid Mech. 613, 411.Google Scholar