Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T03:47:45.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of osmotic pressure on the stability of Taylor vortices

Published online by Cambridge University Press:  06 January 2022

Rouae Ben Dhia ,
Nils Tilton  and
Denis Martinand Open the ORCID record for Denis Martinand [Opens in a new window]
Rouae Ben Dhia
Affiliation:
Aix-Marseille Univ, CNRS, Centrale Marseille, M2P2, Marseille, France
Nils Tilton
Affiliation:
Mechanical Engineering, Colorado School of Mines, Golden, CO 80401, USA
Denis Martinand*
Affiliation:
Aix-Marseille Univ, CNRS, Centrale Marseille, M2P2, Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

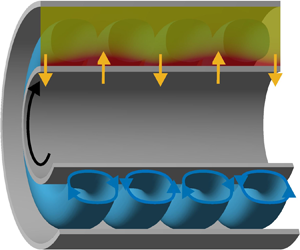
We use linear stability analysis and direct numerical simulations to investigate the coupling between centrifugal instabilities, solute transport and osmotic pressure in a Taylor–Couette configuration that models rotating dynamic filtration devices. The geometry consists of a Taylor–Couette cell with a superimposed radial throughflow of solvent across two semi-permeable cylinders. Both cylinders totally reject the solute, inducing the build-up of a concentration boundary layer. The solute retroacts on the velocity field via the osmotic pressure associated with the concentration differences across the semi-permeable cylinders. Our results show that the presence of osmotic pressure strongly alters the dynamics of the centrifugal instabilities and substantially reduces the critical conditions above which Taylor vortices are observed. It is also found that this enhancement of the hydrodynamic instabilities eventually plateaus as the osmotic pressure is further increased. We propose a mechanism to explain how osmosis and instabilities cooperate and develop an analytical criterion to bound the parameter range for which osmosis fosters the hydrodynamic instabilities.

JFM classification

Instability: Taylor-Couette flow Mass Transport: Coupled diffusion and flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 933 , 25 February 2022 , A51
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahmad, A.L. & Lau, K.K. 2006 Impact of different spacer filaments geometries on 2D unsteady hydrodynamics on concentration polarization in spiral wound membrane channel. J. Membr. Sci. 286, 77–92.CrossRefGoogle Scholar
Akonur, A. & Lueptow, R.M. 2002 Chaotic mixing and transport in wavy Taylor–Couette flow. Physica D 167, 183–196.CrossRefGoogle Scholar
Aljishi, M.F., Ruo, A.C., Park, J.H., Nasser, B., Kim, W.S. & Joo, Y.L. 2013 Effect of flow structure at the onset of instability on barium sulfate precipitation in Taylor–Couette crystallizers. J. Cryst. Growth 373, 20–31.CrossRefGoogle Scholar
Andereck, C.D., Liu, S.S. & Swinney, H.L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Bahl, S.K. 1970 Stability of viscous flow between two concentric rotating porous cylinders. Def. Sci. J. 20, 89–95.Google Scholar
Beaudoin, G. & Jaffrin, M.Y. 1989 Plasma filtration in Couette flow membrane devices. Artif. Organs 13 (1), 43–51.CrossRefGoogle ScholarPubMed
Beavers, G.S. & Joseph, D.D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207.CrossRefGoogle Scholar
Belfort, G., Mikulasek, P., Pimbley, J.M. & Chung, K.Y. 1993 a Diagnosis of membrane fouling using a rotating annular filter. 2. Dilute particule suspension of known particule size. J. Membr. Sci. 77 (1), 23–39.CrossRefGoogle Scholar
Belfort, G., Pimbley, J.M., Greiner, A. & Chung, K.Y. 1993 b Diagnosis of membrane fouling using a rotating annular filter. 1. Cell culture media. J. Membr. Sci. 77 (1), 1–22.CrossRefGoogle Scholar
Bernales, B., Haldenwang, P., Guichardon, P. & Ibaseta, N. 2017 Prandtl model for concentration polarization and osmotic counter-effects in a 2-D membrane channel. Desalination 404, 341–359.CrossRefGoogle Scholar
Bilson, M. & Bremhorst, K. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 579, 227–270.CrossRefGoogle Scholar
Cole, J.A. 1976 Taylor vortex instability and annulus-length effects. J. Fluid Mech. 75, 1–15.CrossRefGoogle Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.CrossRefGoogle Scholar
Davey, A., DiPrima, R.C. & Stuart, J.T. 1968 On the instability of Taylor vortices. J. Fluid Mech. 31, 17–52.CrossRefGoogle Scholar
Ghaffour, N., Missimer, T.M. & Amy, G.L. 2013 Technical review and evaluation of the economics of water desalination: current and future challenges for better water supply sustainability. Desalination 309, 197–207.CrossRefGoogle Scholar
Giordano, R.L.C., Giordano, R.C. & Cooney, C.L. 2000 a Performance of a continuous Taylor–Couette–Poiseuille vortex flow enzymic reactor with suspended particles. Process Biochem. 35, 1093–1101.CrossRefGoogle Scholar
Giordano, R.L.C., Giordano, R.C., Prazeres, D.M.F. & Cooney, C.L. 2000 b Analysis of a Taylor–Poiseuille vortex flow reactor — II: reactor modeling and performance assessment using glucose-fructose isomerization as test reaction. Chem. Engng Sci. 55, 3611–3626.CrossRefGoogle Scholar
Haidari, A.H., Heijman, S.G.J. & van der Meer, W.G.J. 2016 Vizualization of hydraulic conditions inside the feed channel of Reverse Osmosis: a practical comparison of velocity between empty and spacer-filled channel. Water Res. 106, 232–241.CrossRefGoogle Scholar
Haidari, A.H., Heijman, S.G.J. & van der Meer, W.G.J. 2018 a Effect of spacer configuration on hydraulic conditions using PIV. Sep. Purif. Technol. 199, 9–19.CrossRefGoogle Scholar
Haidari, A.H., Heijman, S.G.J. & van der Meer, W.G.J. 2018 b Optimal design of spacers in reverse osmosis. Sep. Purif. Technol. 192, 441–456.CrossRefGoogle Scholar
Haldenwang, P., Guichardon, P., Chiavassa, G. & Ibaseta, N. 2010 Exact solution to mass transfer in berman flow: application to concentration polarization combined with osmosis in crossflow membrane filtration. Intl J. Heat Mass Transfer 53, 3898–3904.CrossRefGoogle Scholar
Hallström, B. & Lopez-Leiva, M. 1978 Decription of a rotating ultrafiltration module. Desalination 24 (1–3), 273–279.CrossRefGoogle Scholar
Koshmieder, E.L. 1993 Bénard Cells and Taylor Vortices. Cambridge University Press.Google Scholar
Kroner, K.H. & Nissinen, V. 1988 Dynamic filtration of microbial suspension using an axially rotating filter. J. Membr. Sci. 36, 85–100.CrossRefGoogle Scholar
Lopes, G.H., Bernales, B., Ibaseta, N., Guichardon, P. & Haldenwang, P. 2012 Prediction of permeate flux and rejection rate in RO and NF membrane processes: numerical modelling of hydrodynamics and mass transfer coupling. Procedia Engng 44, 1934–1936.CrossRefGoogle Scholar
Lou, J., Johnston, J., Cath, T.Y., Martinand, D. & Tilton, N. 2021 Computational fluid dynamics simulations of steady and unsteady mixing in spacer-filled direct contact membrane distillation channels. J. Membr. Sci. 622, 118931.CrossRefGoogle Scholar
Lou, J., Vanneste, J., Decaluwe, S.C., Cath, T.Y. & Tilton, N. 2019 Computational fluid dynamics simulations of polarization phenomena in direct contact membrane distillation. J. Membr. Sci. 591, 117150.CrossRefGoogle Scholar
Lueptow, R.M. & Hajiloo, A. 1995 Flow in a rotating membrane plasma separator. Am. Soc. Artif. Intern. Organs 41 (2), 182–188.CrossRefGoogle Scholar
Lyster, E., Au, J., Rallo, R., Giralt, F. & Cohen, Y. 2009 Coupled 3-D hydrodynamics and mass transfer analysis of mineral scaling-induced flux decline in a laboratory plate-and-frame reverse osmosis membrane module. J. Membr. Sci. 339, 39–48.CrossRefGoogle Scholar
Mansouri, J., Harrisson, S. & Chen, V. 2010 Strategies for controlling biofouling in membrane filtration systems: challenges and opportunities. J. Mater. Chem. 20, 4567–4586.CrossRefGoogle Scholar
Marcus, P.S. 1984 Simulation of Taylor–Couette flow. Part 2. Numerical results for wavy vortex flow with one travelling wave. J. Fluid Mech. 146, 65–113.CrossRefGoogle Scholar
Margaritis, A. & Wilke, C.R. 1978 The Rotorfermentor. I. Descritpion of the apparatus power requirements, and mass transfer characteristics. Biotechnol. Bioengng 20 (5), 709–726.CrossRefGoogle Scholar
Martinand, D., Serre, E. & Lueptow, R.M. 2009 Absolute and convective instability of cylindrical Couette flow with axial and radial flows. Phys. Fluids 21, 104102.CrossRefGoogle Scholar
Martinand, D., Serre, E. & Lueptow, R.M. 2017 Weakly nonlinear analysis of cylindrical Couette flow with axial and radial flows. J. Fluid Mech. 824, 438–476.CrossRefGoogle Scholar
Min, K. & Lueptow, R.M. 1994 Hydrodynamic stability of viscous flow between rotating porous cylinders with radial flow. Phys. Fluids 6 (1), 144–151.CrossRefGoogle Scholar
Miyashita, T. & Senna, M. 1993 Development of Taylor Vortices in a concentrated suspension comprising monodispersed microspheres. J. Colloid Interface Sci. 155, 290–296.CrossRefGoogle Scholar
Nayar, K.G., Sharqawy, M.H. & Lienhard, J.H. 2018 Seawater Thermophysical Properties Library. Tech. Rep. MIT, http://web.mit.edu/seawater (last access 2021-05-17).Google Scholar
Nemri, M., Climent, E., Charton, S., Lanoe, J-Y. & Ode, D. 2013 Experimental and numerical investigation on mixing and axial dispersion in Taylor–Couette flow patterns. Chem. Engng Res. Des. 91, 2346–2354.CrossRefGoogle Scholar
Ohashi, K., Tashiro, K., Kushiya, F., Matsumoto, T., Yoshida, S., Endo, M., Horio, T., Osawa, K. & Sakai, K. 1988 Rotation-induced Taylor vortex enhances filtrate flux in plasma separation. Trans. Am. Soc. Artif. Intern. Organs 34 (3), 300–307.Google ScholarPubMed
Ostilla-Monico, R., van der Poel, E.P., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.CrossRefGoogle Scholar
Raspo, I., Hughes, S., Serre, E., Randriamampianina, A. & Bontoux, P. 2002 A spectral projection method for the simulation of complex three-dimensional rotating flows. Comput. Fluids 31 (4–7), 745–767.CrossRefGoogle Scholar
Sablani, S.S., Goosen, M.F.A., Al-Belush, R. & Wilf, M. 2001 Concentration polarization in ultrafiltration and reverse osmosis: a critical review. Desalination 141, 269–289.CrossRefGoogle Scholar
Schwille, J.A., Mitra, D. & Lueptow, R.M. 2002 Design parameters for rotating filtration. J. Membr. Sci. 204 (1–2), 53–65.CrossRefGoogle ScholarPubMed
Serre, E., Sprague, M.A. & Lueptow, R.M. 2008 Stability of Taylor–Couette flow in a finite-length cavity with radial through-flow. Phys. Fluids 20 (3), 034106.CrossRefGoogle Scholar
Taylor, G.I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. A 223, 289–343.Google Scholar
Tilton, N. & Martinand, D. 2018 Taylor–Couette–Poiseuille flow with a weakly permeable inner cylinder: absolute instabilities and selection of global modes. J. Fluid Mech. 849, 741–776.CrossRefGoogle Scholar
Tilton, N., Martinand, D., Serre, E. & Lueptow, R. 2012 Incorporating Darcy's law for pure solvent flow through porous tubes: asymptotic solution and numerical simulation. AIChE J. 58, 2030–2044.CrossRefGoogle Scholar
Tilton, N., Martinand, D., Serre, E. & Lueptow, R.M. 2010 Pressure-driven radial flow in a Taylor–Couette cell. J. Fluid Mech. 660, 527–537.CrossRefGoogle Scholar
Tilton, N., Serre, E., Martinand, D. & Lueptow, R.M. 2014 A 3D pseudospectral algorithm for fluid flows with permeable walls. Application to filtration. Comput. Fluids 93, 129–145.CrossRefGoogle Scholar
Vanel, J.M., Peyret, R. & Bontoux, P. 1986 A pseudospectral solution of vorticity streamfunction equations using the influence matrix technique. In Numerical Methods for Fluid Dynamics II (ed. K.W. Morton & M.J. Baines), pp. 463–475. Clarendon Press.Google Scholar
van Wagner, E.M., Sagle, A.C., Sharma, M.M. & Freeman, B.D. 2009 Effect of crossflow testing conditions, including feed pH and continuous feed filtration, on commercial reverse osmosis membrane performance. J. Membr. Sci. 345, 97–109.CrossRefGoogle Scholar
Wang, J., Dlamini, D.S., Mishra, A.K., Pendergast, M.T.M., Wong, M.C.Y., Mamba, B.B., Freger, V., Verliefde, A.R.D. & Hoek, E.M.V. 2014 A critical review of transport through osmotic membranes. J. Membr. Sci. 454, 516–537.CrossRefGoogle Scholar