Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T21:50:36.811Z Has data issue: false hasContentIssue false
  • English
  • Français

The impact of imperfect heat transfer on the convective instability of a thermal boundary layer in a porous media

Published online by Cambridge University Press:  30 March 2016

Joseph Hitchen  and
Andrew J. Wells
Joseph Hitchen*
Affiliation:
Atmospheric, Oceanic and Planetary Physics, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU, UK
Andrew J. Wells
Affiliation:
Atmospheric, Oceanic and Planetary Physics, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider convective instability in a deep porous medium cooled from above with a linearised thermal exchange at the upper surface, thus determining the impact of using a Robin boundary condition, in contrast to previous studies using a Dirichlet boundary condition. With the linearised surface exchange, the thermal flux out of the porous layer depends linearly on the temperature difference between the effective temperature of a heat sink at the upper boundary and the temperature at the surface of the porous layer. The rate of this exchange is characterised by a dimensionless Biot number, $\mathit{Bi}$, determined by the effective thermal conductivity of exchange with the heat sink relative to the physical thermal conductivity of the porous layer. For a given temperature difference between the heat sink at the upper boundary and deep in the porous medium, we find that imperfectly cooled layers with finite Biot numbers are more stable to convective instabilities than perfectly cooled layers which have large, effectively infinite Biot numbers. Two regimes of behaviour were determined with contrasting stability behaviour and characteristic scales. When the Biot number is large the near-perfect heat transfer produces small corrections of order 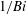$1/\mathit{Bi}$ to the perfectly conducting behaviour found when the Biot number is infinite. In the insulating limit as the Biot number approaches zero, a different behaviour was found with significantly larger scales for the critical wavelength and depth of convection both scaling proportional to 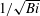$1/\sqrt{\mathit{Bi}}$.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection Convection: Convection in porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 794 , 10 May 2016 , pp. 154 - 174
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barletta, A. & Storesletten, L. 2011 Onset of convective rolls in a circular porous duct with external heat transfer to a thermally stratified environment. Intl J. Therm. Sci. 50 (8), 1374–1384.CrossRefGoogle Scholar
Barletta, A. & Storesletten, L. 2012 Onset of convection in a porous rectangular channel with external heat transfer to upper and lower fluid environments. Trans. Porous Med. 94 (3), 659–681.Google Scholar
Barletta, A. & Storesletten, L. 2013 Effect of a finite external heat transfer coefficient on the Darcy–Bénard instability in a vertical porous cylinder. Phys. Fluids 25 (4), 044101.Google Scholar
Barletta, A., Tyvand, P. A. & Nygård, H. S. 2015 Onset of thermal convection in a porous layer with mixed boundary conditions. J. Engng Maths 91 (1), 105–120.Google Scholar
Beckermann, C., Gu, J. P. & Boettinger, W. J. 2000 Development of a freckle predictor via Rayleigh number method for single-crystal nickel-base superalloy castings. Metall. Mater. Trans. A 31A, 2545–2557.CrossRefGoogle Scholar
Caltagirone, J.-P. 1980 Stability of a saturated porous layer subject to a sudden rise in surface temperature: comparison between the linear and energy methods. Q. J. Mech. Appl. Maths 33 (1), 47–58.CrossRefGoogle Scholar
Carslaw, H. S. & Jaeger, J. C. 1959 Conduction of Heat in Solids. Oxford University Press.Google Scholar
Copley, S. M., Giamei, A. F., Johnson, S. M. & Hornbeck, M. F. 1970 Origin of freckles in unidirectionally solidified castings. Metall. Trans. 1, 2193–2204.CrossRefGoogle Scholar
van Dam, R. L., Simmons, C. T., Hyndman, D. W. & Wood, W. W. 2009 Natural free convection in porous media: first field documentation in groundwater. Geophys. Res. Lett. 36, L11403.Google Scholar
Emami-Meybodi, H., Hassanzadeh, H., Green, C. P. & Ennis-King, J. 2015 Convective dissolution of $\text{CO}_{2}$ in saline aquifers: progress in modeling and experiments. Intl J. Greenh. Gas Control 40, 238–266.Google Scholar
Emms, P. W. & Fowler, A. C. 1994 Compositional convection in the solidification of binary alloys. J. Fluid Mech. 262, 111–139.Google Scholar
Ennis-King, J., Preston, I. & Paterson, L. 2005 Onset of convection in anisotropic porous media subject to a rapid change in boundary conditions. Phys. Fluids 17, 084107.Google Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2006 Stability of a fluid in a horizontal saturated porous layer: effect of non-linear concentration profile, initial, and boundary conditions. Trans. Porous Med. 65, 193–221.Google Scholar
Hurle, D. T. J., Jakeman, E. & Pike, E. R. 1967 On the solution of the Bénard problem with boundaries of finite conductivity. Proc. R. Soc. Lond. A 296 (1447), 469–475.Google Scholar
Hwang, I. G. & Chung, C. K. 2008 Onset of convection in a porous mush during binary solidification. Korean J. Chem. Engng 25 (2), 199–202.Google Scholar
Kim, M. C. & Choi, C. K. 2012 Linear stability analysis on the onset of buoyancy-driven convection in liquid-saturated porous medium. Phys. Fluids 24, 044102.Google Scholar
Kubitschek, J. P. & Weidman, P. D. 2003 Stability of a fluid-saturated porous medium heated from below by forced convection. Intl J. Heat Mass Transfer 46 (19), 3697–3705.Google Scholar
Maykut, G. A. 1978 Energy exchange over young sea ice in the central Arctic. J. Geophys. Res. 83 (C7), 3646–3658.Google Scholar
Nield, D. A. & Bejan, A. 2013 Convection in Porous Media, 4th edn. Springer.CrossRefGoogle Scholar
Nygård, H. S. & Tyvand, P. A. 2010 Onset of convection in a porous box with partly conducting and partly penetrative sidewalls. Trans. Porous Med. 84 (1), 55–73.Google Scholar
Rees, D. A. S., Selim, A. & Ennis-King, J. P. 2008 The instability of unsteady boundary layers in porous media. In Emerging Topics in Heat and Mass Transfer in Porous Media (ed. Vadász, P.), Theory and Applications of Transport in Porous Media, vol. 22, pp. 85–110. Springer.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.CrossRefGoogle Scholar
Slim, A. C. & Ramakrishnan, T. S. 2010 Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 22, 124103.CrossRefGoogle Scholar
Tilton, N., Daniel, D. & Riaz, A. 2013 The initial transient period of gravitationally unstable diffusive boundary layers developing in porous media. Phys. Fluids 25, 092107.Google Scholar
Tilton, N. & Riaz, A. 2014 Nonlinear stability of gravitationally unstable, transient, diffusive boundary layers in porous media. J. Fluid Mech. 745, 251–278.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.CrossRefGoogle Scholar
Wells, A. J., Wettlaufer, J. S. & Orszag, S. A. 2011 Brine fluxes from growing sea ice. Geophys. Res. Lett. 38, L04501.Google Scholar
Wettlaufer, J. S., Worster, M. G. & Huppert, H. E. 2000 Solidification of leads: theory, experiment and field observations. J. Geophys. Res. 105, 1123–1134.Google Scholar
Wilkes, K. E. 1995 Onset of natural convection in a horizontal porous medium with mixed thermal boundary conditions. Trans. ASME J. Heat Transfer 117, 543–547.Google Scholar