Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T15:21:33.107Z Has data issue: false hasContentIssue false
  • English
  • Français

The impact of a deep-water plunging breaker on a wall with its bottom edge close to the mean water surface

Published online by Cambridge University Press:  04 April 2018

An Wang Open the ORCID record for An Wang [Opens in a new window] ,
Christine M. Ikeda-Gilbert ,
James H. Duncan Open the ORCID record for James H. Duncan [Opens in a new window] ,
Daniel P. Lathrop ,
Mark J. Cooker  and
Anne M. Fullerton
An Wang
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
Christine M. Ikeda-Gilbert
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
James H. Duncan*
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
Daniel P. Lathrop
Affiliation:
Department of Physics, University of Maryland, College Park, MD 20742, USA
Mark J. Cooker
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK
Anne M. Fullerton
Affiliation:
Naval Surface Warfare Center, Carderock Division, Bethesda, MD 20817, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The impact of a deep-water plunging breaker on a finite height two-dimensional structure with a vertical front face is studied experimentally. The structure is located at a fixed horizontal position relative to a wave maker and the structure’s bottom surface is located at a range of vertical positions close to the undisturbed water surface. Measurements of the water surface profile history and the pressure distribution on the front surface of the structure are performed. As the vertical position, 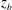$z_{b}$ (the $z$ axis is positive up and 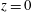$z=0$ is the mean water level), of the structure’s bottom surface is varied from one experimental run to another, the water surface evolution during impact can be categorized into three classes of behaviour. In class I, with 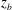$z_{b}$ in a range of values near 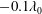$-0.1\unicode[STIX]{x1D706}_{0}$, where 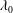$\unicode[STIX]{x1D706}_{0}$ is the nominal wavelength of the breaker, the behaviour of the water surface is similar to the flip-through phenomena first described in studies with shallow water and a structure mounted on the sea bed. In the present work, it is found that the water surface between the front face of the structure and the wave crest is well fitted by arcs of circles with a decreasing radius and downward moving centre as the impact proceeds. A spatially and temporally localized high-pressure region was found on the impact surface of the structure and existing theory is used to explore the physics of this phenomenon. In class II, with 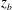$z_{b}$ in a range of values near the mean water level, the bottom of the structure exits and re-enters the water phase at least once during the impact process. These air–water transitions generate large-amplitude ripple packets that propagate to the wave crest and modify its behaviour significantly. At 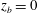$z_{b}=0$, all sensors submerged during the impact record a nearly in-phase high-frequency pressure oscillation indicating possible air entrainment. In class III, with 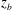$z_{b}$ in a range of values near 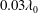$0.03\unicode[STIX]{x1D706}_{0}$, the bottom of the structure remains in air before the main crest hits the bottom corner of the structure. The subsequent free surface behaviour is strongly influenced by the instantaneous momentum of the local flow just before impact and the highest wall pressures of all experimental conditions are found.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave breaking
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 680 - 721
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Kevin T. Crofton Department of Aerospace and Ocean Engineering, Virginia Tech, Blacksburg, VA 24061, USA.

References

Bagnold, R. A. 1939 Interim report on wave-pressure research. J. Inst. Civil Engng 12, 202–226.Google Scholar
Blackmore, P. A. & Hewson, P. J. 1984 Experiments on full-scale wave impact pressures. Coast. Engng 8 (4), 331–346.Google Scholar
Bredmose, H., Bullock, G. N. & Hogg, A. J. 2015 Violent breaking wave impacts. Part 3. Effects of scale and aeration. J. Fluid Mech. 765, 82–113.Google Scholar
Bredmose, H., Peregrine, D. H. & Bullock, G. N. 2009 Violent breaking wave impacts. Part 2: modelling the effect of air. J. Fluid Mech. 641, 389–430.Google Scholar
Bullock, G. N., Crawford, A. R., Hewson, P. J., Walkden, M. J. A. & Bird, P. A. D. 2001 The influence of air and scale on wave impact pressures. Coast. Engng 42 (4), 291–312.Google Scholar
Bullock, G. N., Obhrai, C., Peregrine, D. H. & Bredmose, H. 2007 Violent breaking wave impacts. part 1: results from large-scale regular wave tests on vertical and sloping walls. Coast. Engng 54 (8), 602–617.Google Scholar
Chan, E. S. & Melville, W. K. 1988 Deep-water plunging wave pressures on a vertical plane wall. Proc. R. Soc. Lond. A 417 (1852), 95–131.Google Scholar
Cooker, M. J. 2002 Unsteady pressure fields which precede the launch of free–surface liquid jets. Proc. R. Soc. Lond. A 458 (2018), 473–488.Google Scholar
Cooker, M. J. & Peregrine, D. H. 1992 Violent motion as near breaking waves meet a vertical wall. In Breaking Waves: IUTAM Symp., Sydney 1991 (ed. Banner, M. L. & Grimshaw, R. H. J.), pp. 291–297. IUTAM, Springer.Google Scholar
Day, R. F., Hinch, E. J. & Lister, J. R. 1998 Self-similar capillary pinchoff of an inviscid fluid. Phys. Rev. Lett. 80 (4), 704–707.Google Scholar
Dommermuth, D. G., Yue, D. K. P., Lin, W. M., Rapp, R. J., Chan, E. S. & Melville, W. K. 1988 Deep-water plunging breakers: a comparison between potential theory and experiments. J. Fluid Mech. 189, 423–442.Google Scholar
Duncan, J. H., Qiao, H., Philomin, V. & Wenz, A. 1999 Gentle spilling breakers: crest profile evolution. J. Fluid Mech. 379, 191–222.Google Scholar
Kirkgöz, M. S. 1991 Impact pressure of breaking waves on vertical and sloping walls. Ocean Engng 18 (1–2), 45–59.Google Scholar
Leppinen, D. & Lister, J. R. 2003 Capillary pinch-off in inviscid fluids. Phys. Fluids 15 (2), 568–578.Google Scholar
Liu, X. & Duncan, J. H. 2006 An experimental study of surfactant effects on spilling breakers. J. Fluid Mech. 567, 433–455.Google Scholar
Longuet-Higgins, M. S. 1974 Breaking waves in deep or shallow water. In Proc. 10th Symp. on Naval Hydrodynamics (ed. Cooper, R. D. & Doroff, S. D.), pp. 597–605. Office of Naval Research.Google Scholar
Longuet-Higgins, M. S. 1993 Highly accelerated, free-surface flows. J. Fluid Mech. 248, 449–475.Google Scholar
Longuet-Higgins, M. S. 2001 Vertical jets from standing waves. Proc. R. Soc. Lond. A 457 (2006), 495–510.Google Scholar
Longuet-Higgins, M. S. & Cokelet, E. D. 1976 The deformation of steep surface waves on water. i. a numerical method of computation. Proc. R. Soc. Lond. A 350 (1660), 1–26.Google Scholar
Longuet-Higgins, M. S. & Oguz, H. 1995 Critical microjets in collapsing cavities. J. Fluid Mech. 290, 183–201.Google Scholar
Longuet-Higgins, M. S. & Oguz, H. N. 1997 Critical jets in surface waves and collapsing cavities. Phil. Trans. R. Soc. Lond. A 355 (1724), 625–639.Google Scholar
Lugni, C., Brocchini, M. & Faltinsen, O. M. 2006 Wave impact loads: the role of the flip-through. Phys. Fluids 18 (12), 122101.Google Scholar
Lugni, C., Brocchini, M. & Faltinsen, O. M. 2010a Evolution of the air cavity during a depressurized wave impact. ii. the dynamic field. Phys. Fluids 22 (5), 056102.Google Scholar
Lugni, C., Miozzi, M., Brocchini, M. & Faltinsen, O. M. 2010b Evolution of the air cavity during a depressurized wave impact. I. The kinematic flow field. Phys. Fluids 22 (5), 056101.Google Scholar
Peregrine, D. H. 2003 Water-wave impact on walls. Annu. Rev. Fluid Mech. 35 (1), 23–43.Google Scholar
Peregrine, D. H. & Thais, L. 1996 The effect of entrained air in violent water wave impacts. J. Fluid Mech. 325, 377–398.Google Scholar
Perlin, M., He, J. & Bernal, L. P. 1996 An experimental study of deep water plunging breakers. Phys. Fluids 8 (9), 2365–2374.Google Scholar
Plesset, M. S. & Prosperetti, A. 1977 Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 9 (1), 145–185.Google Scholar
Rapp, R. J. & Melville, W. K. 1990 Laboratory measurements of deep-water breaking waves. Phil. Trans. R. Soc. Lond. A 331 (1622), 735–800.Google Scholar
Wang, A.2017 On the impact between a water free surface and a rigid structure. PhD thesis, University of Maryland College Park.Google Scholar
Zeff, B. W., Kleber, B., Fineberg, J. & Lathrop, D. P. 2000 Singularity dynamics in curvature collapse and jet eruption on a fluid surface. Nature 403 (6768), 401–404.Google Scholar
Zhang, S., Duncan, J. H. & Chahine, G. L. 1993 The final stage of the collapse of a cavitation bubble near a rigid wall. J. Fluid Mech. 257, 147–181.Google Scholar
Zhang, S., Yue, D. K. P. & Tanizawa, K. 1996 Simulation of plunging wave impact on a vertical wall. J. Fluid Mech. 327, 221–254.Google Scholar
Supplementary material: File

Wang et al. supplementay material

Supplementary data

Download Wang et al. supplementay material(File)
File 36.5 MB

Wang et al. supplementary movie 1

LIF high-speed movie of the breaker in open water (corresponding to figure 4).

Download Wang et al. supplementary movie 1(Video)
Video 14.8 MB

Wang et al. supplementary movie 2

LIF high-speed movie of the water surface profile for $z_b = -0.113\lambda_0$ (corresponding to figure 5).

Download Wang et al. supplementary movie 2(Video)
Video 18.4 MB

Wang et al. supplementary movie 3

LIF high-speed movie of the water surface profile for $z_b = 0$ (corresponding to figure 9).

Download Wang et al. supplementary movie 3(Video)
Video 3.2 MB

Wang et al. supplementary movie 4

LIF high-speed movie of the water surface profile for $z_b = 0.022\lambda_0$ (corresponding to figure 13).

Download Wang et al. supplementary movie 4(Video)
Video 2.6 MB

Wang et al. supplementary movie 5

LIF high-speed movie of the water surface profile for $z_b = 0.043\lambda_0$ (corresponding to figure 14).

Download Wang et al. supplementary movie 5(Video)
Video 2.7 MB

Wang et al. supplementary movie 6

LIF high-speed movie with a close-up view of the water surface profile for $z_b = -0.113\lambda_0$ (corresponding to figure 22).

Download Wang et al. supplementary movie 6(Video)
Video 1.1 MB