Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T22:43:39.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Identification of Lagrangian coherent structures in a turbulent boundary layer

Published online by Cambridge University Press:  11 July 2013

Z. D. Wilson ,
M. Tutkun  and
R. B. Cal
Z. D. Wilson
Affiliation:
Department of Mechanical and Materials Engineering, Portland State University, Portland, OR 97201, USA
M. Tutkun
Affiliation:
Department of Process and Fluid Flow Technology, Institute for Energy Technology, 2027 Kjeller, Norway Université Lille Nord de France, École Centrale de Lille, 59655 Villeneuve d’Ascq, France
R. B. Cal*
Affiliation:
Department of Mechanical and Materials Engineering, Portland State University, Portland, OR 97201, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

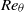Lagrangian coherent structures (LCS) of a turbulent boundary layer at ${\mathit{Re}}_{\theta } $ of 9800 are identified in a plane parallel to the wall at 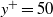${y}^{+ } = 50$. Three-component high-speed stereo particle image velocimetry measurements on a two-dimensional rectangular plane are used for the analysis. The velocity field is extended in the streamwise direction, using Taylor’s frozen field hypothesis. A computational approach utilizing the variational theory of hyperbolic Lagrangian coherent structures is applied to the domain and trajectories are computed using the extended field. The method identified both attracting and repelling Lagrangian coherent structures. There are no apparent differences in distribution of size, orientation and location of attracting and repelling structures. Hyperbolic behaviour appeared in the fluid at and around points of intersection between the attracting and repelling Lagrangian coherent structures. The network of curves identifying distinct regions of coherent flow patterns is displayed in observed relationship between the arrangement of Lagrangian coherent structures and various Eulerian fields.

JFM classification

Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 728 , 10 August 2013 , pp. 396 - 416
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 1–54.CrossRefGoogle Scholar
Álamo, C. J. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
Arnold, V. I. 1973 Ordinary Differential Equations. MIT Press.Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.CrossRefGoogle Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.CrossRefGoogle Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2, 765–777.Google Scholar
Chong, P., JinJun, W. & Cao, Z. 2009 Identification of Lagrangian coherent structures in the turbulent boundary layer. Sci. China G: Phys. Mech. Astron. 52, 248–257.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Farazmand, M. & Haller, G. 2012a Computing Lagrangian coherent structures from their variational theory. Chaos 22, 013128–1–12.CrossRefGoogle ScholarPubMed
Farazmand, M. & Haller, G. 2012b Erratum and addendum to ‘A variational theory of hyperbolic Lagrangian coherent structures. Physica D 240, 7’. Physica D 241, 439–441.Google Scholar
Focaut, J. M., Coudert, S., Kostas, J., Stanislas, M., Braud, P., Fourment, C., Delville, J., Tutkun, M., Johansson, P. & George, W. K. 2007 Study of the unsteady aspects of turbulence in the near wall region of a boundary layer using High Speed SPIV, In 7th International Symposium on Particle Image Velocimetry.Google Scholar
Garth, C., Gerhardt, F., Tricoche, X. & Hagen, H. 2007 Efficient computation and visualization of coherent structures in fluid flow applications. IEEE Trans. Vis. Comput. Graphics 13 (6), 1464–1471.CrossRefGoogle ScholarPubMed
Green, M. A., Rowley, C. W. & Haller, G. 2007 Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 572, 111–120.CrossRefGoogle Scholar
Haller, G. 2001 Distinguished material surfaces and coherent structures in 3D fluid flows. Physica D 149, 248–277.CrossRefGoogle Scholar
Haller, G. 2005 An objective definition of a vortex. J. Fluid Mech. 525, 1–26.CrossRefGoogle Scholar
Haller, G. 2011 A variational theory of hyperbolic Lagrangian coherent structures. Physica D 240, 574–598.CrossRefGoogle Scholar
Hinze, J. O. 1959 Turbulence. McGraw Hill.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases, 2. Proceedings of the 1988 Summer Program CTR-S88, pp. 193–208. Center for Turbulence Research, Stanford, CA.Google Scholar
Jeong, J. & Hussein, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Lukens, S., Yang, X. & Fauci, L. 2010 Using Lagrangian coherent structures to analyse fluid mixing by cilia. Chaos 20, 017511.Google Scholar
Mathur, M., Haller, G., Peacock, T., Ruppert-Felsot, J. E. & Swinney, H. L. 2007 Uncovering the Lagrangian skeleton of turbulence. Phys. Rev. Lett. 98, 144502.CrossRefGoogle ScholarPubMed
Norgard, G. & Bremer, P.-T. 2012 Second derivative ridges are straight lines and the implications for computing Lagrangian coherent structures. Physica D 241 (18), 1475–1476.CrossRefGoogle Scholar
Peikert, R., Günther, D. & Weinkauf, T. 2013 Comment on ‘Second derivative ridges are straight lines and the implications for computing Lagrangian coherent structures, Physica D 2012.05.006’. Physica D 242 (1), 65–66.CrossRefGoogle Scholar
Peng, J. & Dabiri, J. 2008 An overview of a Lagrangian method for analysis of animal wake dynamics. J. Expl. Biol 211, 280–287.Google Scholar
Pope, S. B. 2011 Simple models of turbulent flows. Phys. Fluids 23, 011301.CrossRefGoogle Scholar
Shadden, S., Lekien, F. & Marsden, J. 2005 Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D 212, 271–304.Google Scholar
Tallapragada, P., Ross, S. D. & Schmale, D. G. 2011 Lagrangian coherent structures are associated with fluctuations in airborne microbial populations. Chaos 21 (3), 033122.CrossRefGoogle ScholarPubMed
Tang, W., Chan, P. W. & Haller, G. 2010 Accurate extraction of Lagrangian coherent structures over finite domains with application to flight data analysis over Hong Kong International Airport. Chaos 20, 017502.CrossRefGoogle ScholarPubMed
Tang, W., Chan, P. W. & Haller, G. 2011 Lagrangian coherent structure analysis of terminal winds detected by lidar. Part i: turbulence structures. J. Appl. Meteorol. Climatol. 50 (2), 325–338.CrossRefGoogle Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. The MIT press.CrossRefGoogle Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proceedings of the 2nd Mid-western Conference on Fluid Mechanics, Ohio State University, pp. 1–19.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar