1. Introduction
To move through viscous fluids, motile micro-organisms exert forces and torques on their environment. Due to their small size, the resulting motion is dominated by the viscous stresses in the fluid, and is well described by the Stokes equation (Lauga & Powers Reference Lauga and Powers2009). The velocity fields created by micro-organisms in this regime can thus be described by a combination of the singular solutions of the Stokes equation, which decay algebraically in space (Spagnolie & Lauga Reference Spagnolie and Lauga2012). The leading singularity for force- and torque-free microswimmers suspended in an infinite viscous fluid is given by a force dipole, which exhibits slow spatial decay, ![]() $r^{-d+1}$, where
$r^{-d+1}$, where ![]() $r$ is the distance from the microorganism and
$r$ is the distance from the microorganism and ![]() $d$ is the dimensionality of space. Such velocity fields are long ranged, and even rather dilute suspensions of microorganisms can therefore exhibit significant fluid motion. Such ‘self-stirring’ in the absence of an external forcing is a strongly non-equilibrium phenomenon characteristic of active matter (Marchetti et al. Reference Marchetti, Joanny, Ramaswamy, Liverpool, Prost, Rao and Simha2013) and results in a unique set of transport and mechanical properties of microswimmer suspensions, such as enhanced diffusivity of tracer particles (Wu & Libchaber Reference Wu and Libchaber2000; Leptos et al. Reference Leptos, Guasto, Gollub, Pesci and Goldstein2009; Miño et al. Reference Miño, Dunstan, Rousselet, Clément and Soto2013; Jepson et al. Reference Jepson, Martinez, Schwarz-Linek, Morozov and Poon2013) and significant changes of the apparent suspension viscosity (Rafaï, Jibuti & Peyla Reference Rafaï, Jibuti and Peyla2010; López et al. Reference López, Gachelin, Douarche, Auradou and Clément2015; Saintillan Reference Saintillan2018; Martinez et al. Reference Martinez2020).
$d$ is the dimensionality of space. Such velocity fields are long ranged, and even rather dilute suspensions of microorganisms can therefore exhibit significant fluid motion. Such ‘self-stirring’ in the absence of an external forcing is a strongly non-equilibrium phenomenon characteristic of active matter (Marchetti et al. Reference Marchetti, Joanny, Ramaswamy, Liverpool, Prost, Rao and Simha2013) and results in a unique set of transport and mechanical properties of microswimmer suspensions, such as enhanced diffusivity of tracer particles (Wu & Libchaber Reference Wu and Libchaber2000; Leptos et al. Reference Leptos, Guasto, Gollub, Pesci and Goldstein2009; Miño et al. Reference Miño, Dunstan, Rousselet, Clément and Soto2013; Jepson et al. Reference Jepson, Martinez, Schwarz-Linek, Morozov and Poon2013) and significant changes of the apparent suspension viscosity (Rafaï, Jibuti & Peyla Reference Rafaï, Jibuti and Peyla2010; López et al. Reference López, Gachelin, Douarche, Auradou and Clément2015; Saintillan Reference Saintillan2018; Martinez et al. Reference Martinez2020).
Depending on the symmetry of their hydrodynamic flow, microswimmers can be divided into two distinct classes: (i) ‘pushers’, which accurately describes most swimming bacteria such as E. coli (Drescher et al. Reference Drescher, Dunkel, Cisneros, Ganguly and Goldstein2011), and (ii) ‘pullers’, whose reversed hydrodynamic flow field is typically exemplified by the alga C. reinhardtii (Guasto, Johnson & Gollub Reference Guasto, Johnson and Gollub2010). While these two flow fields lead to equivalent statistical properties for very dilute microswimmer suspensions, where swimmers can be treated as effectively non-interacting, they lead to strikingly different forms of swimmer–swimmer correlations beyond this limit. Arguably, the most profound effect of such swimmer–swimmer correlations is the transition to large-scale collective motion in elongated pusher-like microswimmers such as bacteria, often referred to as bacterial turbulence (Wensink et al. Reference Wensink, Dunkel, Heidenreich, Drescher, Goldstein, Löwen and Yeomans2012; Dunkel et al. Reference Dunkel, Heidenreich, Dreschner, Wensink, Bär and Goldstein2013). The mechanism of the transition to bacterial turbulence is usually rationalised based on mean-field kinetic theories that take into account the presence of long-range hydrodynamic interactions between microswimmers (Saintillan & Shelley Reference Saintillan and Shelley2008a). For three-dimensional (3-D) suspensions of pusher bacteria, these theories predict the onset of large-scale flows above a well-defined critical microswimmer volume fraction, and identify mutual particle reorientation due to hydrodynamic interactions as the main mechanism behind the instability, while no such instability occurs in 3-D puller suspensions. Even far below the onset of collective motion, the long-ranged hydrodynamic interactions result in strong correlations between microswimmers, leading to an enhancement of the effective tracer diffusivity in pusher suspensions compared with puller suspensions at the same density (Stenhammar et al. Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017; Škultéty et al. Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020).
In practice, observations of 3-D bulk collective flows are complicated by the unavoidable presence of boundaries in experimental set-ups used to study motile microorganisms. Importantly, motile organisms accumulate in close vicinity to solid (Berke et al. Reference Berke, Turner, Berg and Lauga2008) and liquid (Vladescu et al. Reference Vladescu, Marsden, Schwarz-Linek, Martinez, Arlt, Morozov, Marenduzzo, Cates and Poon2014) boundaries, significantly depleting the bulk in between. Therefore, from an experimental perspective, it is much more convenient to study the ensuing collective motion in a layer of microswimmers confined by either type of boundary (Zhang et al. Reference Zhang, Be'er, Florin and Swinney2010; Chen et al. Reference Chen, Dong, Be'er, Swinney and Zhang2012; Sokolov & Aranson Reference Sokolov and Aranson2012; Gachelin et al. Reference Gachelin, Rousselet, Lindner and Clement2014).
The theoretical description of confined microswimmer suspensions is significantly more involved than their bulk fluid counterparts discussed above, as it includes several different effects of the confinement. Firstly, the spatial decay of Stokesian singularities is modified by the presence of boundaries (Spagnolie & Lauga Reference Spagnolie and Lauga2012), with the corresponding far-field fluid velocity being dominated by flow singularities other than the force dipole which is dominant in bulk fluids (Brotto et al. Reference Brotto, Caussin, Lauga and Bartolo2013; Mathijssen et al. Reference Mathijssen, Doostmohammadi, Yeomans and Shendruk2016; Jeanneret, Pushkin & Polin Reference Jeanneret, Pushkin and Polin2019). Secondly, the interactions between microswimmers and the boundaries might depend on the precise shape of the microswimmers, their mechanism of propulsion, surface charge and roughness, etc. The corresponding theory would need to sufficiently resolve the near-field fluid velocity generated by the microswimmers and include appropriate steric interactions (Pessot, Löwen & Menzel Reference Pessot, Löwen and Menzel2018; Zantop & Stark Reference Zantop and Stark2020) and the above-mentioned effects. Such a theory would be very challenging and strongly dependent on the specific system under investigation.
An additional important physical effect inherent to confined systems, although rarely discussed explicitly, is the effective compressibility of the in-plane flow fields generated by a layer of microswimmers (Salbreux, Prost & Joanny Reference Salbreux, Prost and Joanny2009; Jülicher, Grill & Salbreux Reference Jülicher, Grill and Salbreux2018; Maitra Reference Maitra2020; Huang et al. Reference Huang, Hu, Yang, Liu and Zhang2021; Maitra Reference Maitra2023). A similar effect was previously discussed in the context of hydrodynamically interacting colloidal particles under partial confinement (Bleibel et al. Reference Bleibel, Domínguez, Günther, Harting and Oettel2014; Bleibel, Domínguez & Oettel Reference Bleibel, Domínguez and Oettel2015, Reference Bleibel, Domínguez and Oettel2017). To illustrate the point, we consider a force dipole oriented parallel to a solid wall at a distance ![]() $h$ from it. The fluid velocity component
$h$ from it. The fluid velocity component ![]() $\boldsymbol {u}_{\parallel }$ parallel to the wall can be deduced from the image system developed by Blake (Reference Blake1971) for a point force next to a solid boundary with vanishing boundary condition
$\boldsymbol {u}_{\parallel }$ parallel to the wall can be deduced from the image system developed by Blake (Reference Blake1971) for a point force next to a solid boundary with vanishing boundary condition ![]() $\boldsymbol {u}_{\parallel }(z=h) = 0$, and is given by (Spagnolie & Lauga Reference Spagnolie and Lauga2012)
$\boldsymbol {u}_{\parallel }(z=h) = 0$, and is given by (Spagnolie & Lauga Reference Spagnolie and Lauga2012)
 $$\begin{gather} \boldsymbol{u}_{{\parallel}} (\boldsymbol{\mathcal{x}}) = \frac{\kappa}{8{\rm \pi}} \left( \frac{\boldsymbol{\mathcal{x}}}{|\boldsymbol{\mathcal{x}}|^3} \left[ 3 \frac{(\boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}})^2}{|\boldsymbol{\mathcal{x}}|^2} - 1 \right] + \frac{\boldsymbol{\mathcal{x}}}{R^3} \right.\nonumber\\ \left.- \frac{3\boldsymbol{\mathcal{x}} (\boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}})^2 + 6h^2 \left\{\boldsymbol{\mathcal{x}} + 2 \boldsymbol{\mathcal{p}} (\boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}})\right\}}{R^5} + \frac{30 h^2 (\boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}})^2 \boldsymbol{\mathcal{x}}}{R^7} \right). \end{gather}$$
$$\begin{gather} \boldsymbol{u}_{{\parallel}} (\boldsymbol{\mathcal{x}}) = \frac{\kappa}{8{\rm \pi}} \left( \frac{\boldsymbol{\mathcal{x}}}{|\boldsymbol{\mathcal{x}}|^3} \left[ 3 \frac{(\boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}})^2}{|\boldsymbol{\mathcal{x}}|^2} - 1 \right] + \frac{\boldsymbol{\mathcal{x}}}{R^3} \right.\nonumber\\ \left.- \frac{3\boldsymbol{\mathcal{x}} (\boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}})^2 + 6h^2 \left\{\boldsymbol{\mathcal{x}} + 2 \boldsymbol{\mathcal{p}} (\boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}})\right\}}{R^5} + \frac{30 h^2 (\boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}})^2 \boldsymbol{\mathcal{x}}}{R^7} \right). \end{gather}$$
Here, ![]() $\boldsymbol {\mathcal {p}}$ and
$\boldsymbol {\mathcal {p}}$ and ![]() $\boldsymbol {\mathcal {x}}$ are two-dimensional (2-D) vectors that lie in the plane parallel to the wall and denote respectively the dipole orientation and the point where the velocity is evaluated relative to the position of the swimmer. Furthermore,
$\boldsymbol {\mathcal {x}}$ are two-dimensional (2-D) vectors that lie in the plane parallel to the wall and denote respectively the dipole orientation and the point where the velocity is evaluated relative to the position of the swimmer. Furthermore, ![]() $R=\sqrt {|\boldsymbol {\mathcal {x}}|^2 + 4 h^2}$, and
$R=\sqrt {|\boldsymbol {\mathcal {x}}|^2 + 4 h^2}$, and ![]() $\kappa$ is the strength of the dipole. Next, we calculate the total flux of the fluid through a circle of radius
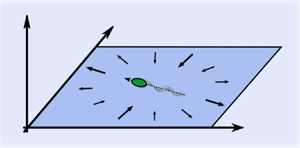
$\kappa$ is the strength of the dipole. Next, we calculate the total flux of the fluid through a circle of radius ![]() $X$ centred on the microswimmer and parallel to the wall, as shown in figure 1, yielding
$X$ centred on the microswimmer and parallel to the wall, as shown in figure 1, yielding
 \begin{equation} \int_{|\boldsymbol{\mathcal{x}}|=X} \,\mathrm{d} \boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{u}_{{\parallel}} = \frac{\kappa}{8 X} \left[ 1 - \frac{X^4-10 X^2 h^2+64h^4}{\left(X^2+4h^2 \right)^{7/2}}X^3\right]. \end{equation}
\begin{equation} \int_{|\boldsymbol{\mathcal{x}}|=X} \,\mathrm{d} \boldsymbol{\mathcal{x}}\boldsymbol{\cdot}\boldsymbol{u}_{{\parallel}} = \frac{\kappa}{8 X} \left[ 1 - \frac{X^4-10 X^2 h^2+64h^4}{\left(X^2+4h^2 \right)^{7/2}}X^3\right]. \end{equation}
Hence, the total flux through an arbitrary circle around a microswimmer is non-zero, indicating that, if we only consider the velocity components parallel to the wall, they represent an effectively compressible velocity field. Moreover, one can show that the prefactor multiplying ![]() $\kappa$ is strictly positive, and the sign of the flux is therefore determined by the sign of the dipolar strength: pushers with
$\kappa$ is strictly positive, and the sign of the flux is therefore determined by the sign of the dipolar strength: pushers with ![]() $\kappa >0$ on average correspond to hydrodynamic sources in the plane parallel to the wall, while pullers with
$\kappa >0$ on average correspond to hydrodynamic sources in the plane parallel to the wall, while pullers with ![]() $\kappa <0$ correspond to hydrodynamic sinks. Therefore, when averaged over all orientations, two pushers advect each other to maximise their mutual separation, while two pullers do the opposite. This argument illustrates that hydrodynamic interactions between dipolar microswimmers moving next to a boundary have a very different nature to their bulk counterparts, which has previously been shown to promote dynamic self-assembly and crystallisation in active-particle systems (Singh & Adhikari Reference Singh and Adhikari2016; Thutupalli et al. Reference Thutupalli, Geyer, Singh, Adhikari and Stone2018). We stress that this effective interaction does not correspond to extra forces or torques on the particles, which is a common assumption when describing ‘dry’ active particles moving on a frictional substrate (ten Hagen et al. Reference ten Hagen, Wittkowski, Takagi, Kümmel, Bechinger and Löwen2015), as the particles immersed in a fluid are strictly force and torque free.
$\kappa <0$ correspond to hydrodynamic sinks. Therefore, when averaged over all orientations, two pushers advect each other to maximise their mutual separation, while two pullers do the opposite. This argument illustrates that hydrodynamic interactions between dipolar microswimmers moving next to a boundary have a very different nature to their bulk counterparts, which has previously been shown to promote dynamic self-assembly and crystallisation in active-particle systems (Singh & Adhikari Reference Singh and Adhikari2016; Thutupalli et al. Reference Thutupalli, Geyer, Singh, Adhikari and Stone2018). We stress that this effective interaction does not correspond to extra forces or torques on the particles, which is a common assumption when describing ‘dry’ active particles moving on a frictional substrate (ten Hagen et al. Reference ten Hagen, Wittkowski, Takagi, Kümmel, Bechinger and Löwen2015), as the particles immersed in a fluid are strictly force and torque free.

Figure 1. Schematic picture of the flow around a single pusher microswimmer restricted to a 2-D plane embedded in a 3-D fluid. Note that the net flow ![]() $\boldsymbol {u}_{\parallel }$ going through the dashed circle is non-zero; in the 2-D plane, pushers therefore, on average, act as fluid sources, while pullers act as effective sinks.
$\boldsymbol {u}_{\parallel }$ going through the dashed circle is non-zero; in the 2-D plane, pushers therefore, on average, act as fluid sources, while pullers act as effective sinks.
The aim of this work is to understand the effect of this in-plane compressibility on collective motion in a minimal setting. We consider a layer of microswimmers restricted to move in an infinitely thin, 2-D plane embedded in a 3-D bulk fluid in the absence of any boundaries, corresponding to taking ![]() $h\to \infty$ in the example above. We assume low number density of microswimmers and approximate their velocity fields by those of 3-D force dipoles. As can be seen from (1.2), even in this limit, the in-plane velocity field generated by the microswimmer is still effectively compressible. Therefore, although this specific set-up is difficult to realise experimentally, it allows us to single out the effect of in-plane compressibility without needing to deal with other effects due to the confinement discussed above.
$h\to \infty$ in the example above. We assume low number density of microswimmers and approximate their velocity fields by those of 3-D force dipoles. As can be seen from (1.2), even in this limit, the in-plane velocity field generated by the microswimmer is still effectively compressible. Therefore, although this specific set-up is difficult to realise experimentally, it allows us to single out the effect of in-plane compressibility without needing to deal with other effects due to the confinement discussed above.
Below, we demonstrate that a 2-D layer of microswimmers embedded in a 3-D fluid is unstable for both pushers and pullers. We show that pusher suspensions are prone to an orientational instability that sets in at the smallest length scale available to the system, while puller suspensions exhibit an instability associated with density variations as a generic consequence of the effective in-plane compressibility.
The paper is organised as follows: in § 2, we present a general kinetic theory describing a dilute suspension of microswimmers interacting through long-range velocity fields. In § 3 we review its predictions for the widely studied case of microswimmers suspended in a 3-D bulk fluid. In § 4 we report on linear stability of a 2-D layer of microswimmers embedded in a 3-D fluid, which constitutes the main novel results of our work. We conclude by summarising our main findings in § 5.
2. Mean-field kinetic theory for microswimmer suspensions
Mean-field kinetic theories of microswimmer suspensions have been extensively discussed in the literature (Saintillan & Shelley Reference Saintillan and Shelley2008a,Reference Saintillan and Shelleyb; Subramanian & Koch Reference Subramanian and Koch2009; Hohenegger & Shelley Reference Hohenegger and Shelley2010; Koch & Subramanian Reference Koch and Subramanian2011; Saintillan & Shelley Reference Saintillan and Shelley2013; Krishnamurthy & Subramanian Reference Krishnamurthy and Subramanian2015), and here we give only a brief summary of their general set-up.
A suspension of ![]() $N$ microswimmers moving autonomously through a viscous fluid is described by the one-particle distribution function
$N$ microswimmers moving autonomously through a viscous fluid is described by the one-particle distribution function ![]() $\varPsi (\boldsymbol {x},\boldsymbol {p},t)$, which defines the instantaneous probability of finding a particle at a spatial position
$\varPsi (\boldsymbol {x},\boldsymbol {p},t)$, which defines the instantaneous probability of finding a particle at a spatial position ![]() $\boldsymbol {x}$ with an orientation given by the unit vector
$\boldsymbol {x}$ with an orientation given by the unit vector ![]() $\boldsymbol {p}$. The distribution function is normalised such that
$\boldsymbol {p}$. The distribution function is normalised such that
Its time evolution is assumed to be governed by the Smoluchowski equation
where Greek superscripts denote Cartesian components of vectors, ![]() $\nabla ^{\alpha } = \partial /\partial x^{\alpha }$,
$\nabla ^{\alpha } = \partial /\partial x^{\alpha }$, ![]() $\partial ^{\alpha } = (\delta ^{\alpha \beta } - p^{\alpha }p^{\beta })\partial / \partial p^{\beta }$, and
$\partial ^{\alpha } = (\delta ^{\alpha \beta } - p^{\alpha }p^{\beta })\partial / \partial p^{\beta }$, and ![]() $\delta ^{\alpha \beta }$ denotes the Kronecker delta;
$\delta ^{\alpha \beta }$ denotes the Kronecker delta; ![]() $\varOmega _d$ is the surface area of a
$\varOmega _d$ is the surface area of a ![]() $d$-sphere of unit radius, where
$d$-sphere of unit radius, where ![]() $d$ is the dimensionality of space, and
$d$ is the dimensionality of space, and ![]() $\lambda$ is the tumbling frequency, as further described below. The deterministic part of the single-swimmer dynamics is described by the following microscopic equations of motion:
$\lambda$ is the tumbling frequency, as further described below. The deterministic part of the single-swimmer dynamics is described by the following microscopic equations of motion:
where dots denote time derivatives. According to (2.3), each particle changes its spatial position due to its own swimming with a constant speed ![]() $v_s$ in the direction of its orientation
$v_s$ in the direction of its orientation ![]() $\boldsymbol {p}$ and due to advection by the fluid flow with velocity
$\boldsymbol {p}$ and due to advection by the fluid flow with velocity ![]() $\boldsymbol {\mathcal {U}}$ at its position
$\boldsymbol {\mathcal {U}}$ at its position ![]() $\boldsymbol {x}$, created by all other microswimmers. Microswimmer orientations change according to Jeffery's equation, (2.4), which describes particle rotation by the gradients of the fluid velocity at its position (Kim & Karrila Reference Kim and Karrila2005). Here,
$\boldsymbol {x}$, created by all other microswimmers. Microswimmer orientations change according to Jeffery's equation, (2.4), which describes particle rotation by the gradients of the fluid velocity at its position (Kim & Karrila Reference Kim and Karrila2005). Here, ![]() $\mathcal {W}^{\alpha \beta }(\boldsymbol {x}) = \tfrac {1}{2} (\nabla ^{\beta } \mathcal {U}^{\alpha }(\boldsymbol {x}) - \nabla ^{\alpha } \mathcal {U}^{\beta }(\boldsymbol {x})),$ and
$\mathcal {W}^{\alpha \beta }(\boldsymbol {x}) = \tfrac {1}{2} (\nabla ^{\beta } \mathcal {U}^{\alpha }(\boldsymbol {x}) - \nabla ^{\alpha } \mathcal {U}^{\beta }(\boldsymbol {x})),$ and ![]() $\mathcal {E}^{\alpha \beta }(\boldsymbol {x}) = \tfrac {1}{2} (\nabla ^{\beta } \mathcal {U}^{\alpha }(\boldsymbol {x}) + \nabla ^{\alpha } \mathcal {U}^{\beta }(\boldsymbol {x}))$ are the vorticity and the rate-of-strain tensors. The Bretherton parameter
$\mathcal {E}^{\alpha \beta }(\boldsymbol {x}) = \tfrac {1}{2} (\nabla ^{\beta } \mathcal {U}^{\alpha }(\boldsymbol {x}) + \nabla ^{\alpha } \mathcal {U}^{\beta }(\boldsymbol {x}))$ are the vorticity and the rate-of-strain tensors. The Bretherton parameter ![]() $B$ encodes the shape of the particle (Kim & Karrila Reference Kim and Karrila2005), with
$B$ encodes the shape of the particle (Kim & Karrila Reference Kim and Karrila2005), with ![]() $B=1$ and
$B=1$ and ![]() $B=0$ respectively corresponding to needle-like and spherical particles. Finally, each microswimmer randomly selects a new orientation (tumbles) with rate
$B=0$ respectively corresponding to needle-like and spherical particles. Finally, each microswimmer randomly selects a new orientation (tumbles) with rate ![]() $\lambda$. This discrete stochastic process cannot be incorporated in the time evolution (2.3) and (2.4) in a straightforward manner, but is readily described within the kinetic theory (Subramanian & Koch Reference Subramanian and Koch2009; Koch & Subramanian Reference Koch and Subramanian2011), as given on the right-hand side of (2.2).
$\lambda$. This discrete stochastic process cannot be incorporated in the time evolution (2.3) and (2.4) in a straightforward manner, but is readily described within the kinetic theory (Subramanian & Koch Reference Subramanian and Koch2009; Koch & Subramanian Reference Koch and Subramanian2011), as given on the right-hand side of (2.2).
The final ingredient of the theory is provided by the relationship between the local velocity field and the one-particle distribution function, given by
Here, ![]() $\boldsymbol {u}(\boldsymbol {x}-\boldsymbol {x}',\boldsymbol {p}')$ is the microscopic velocity field created at
$\boldsymbol {u}(\boldsymbol {x}-\boldsymbol {x}',\boldsymbol {p}')$ is the microscopic velocity field created at ![]() $\boldsymbol {x}$ by a microswimmer located at
$\boldsymbol {x}$ by a microswimmer located at ![]() $\boldsymbol {x}'$ with the orientation
$\boldsymbol {x}'$ with the orientation ![]() $\boldsymbol {p}'$. In the following, we approximate
$\boldsymbol {p}'$. In the following, we approximate ![]() $\boldsymbol {u}$ by the dipolar field generated by two equal and opposite point forces applied to the fluid infinitesimally close to each other (Lauga & Powers Reference Lauga and Powers2009). While this is a good approximation for dilute suspensions of microswimmers in 3-D bulk systems (Lauga & Powers Reference Lauga and Powers2009; Spagnolie & Lauga Reference Spagnolie and Lauga2012; Škultéty et al. Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020), its validity in the context of the present study is discussed in § 5.
$\boldsymbol {u}$ by the dipolar field generated by two equal and opposite point forces applied to the fluid infinitesimally close to each other (Lauga & Powers Reference Lauga and Powers2009). While this is a good approximation for dilute suspensions of microswimmers in 3-D bulk systems (Lauga & Powers Reference Lauga and Powers2009; Spagnolie & Lauga Reference Spagnolie and Lauga2012; Škultéty et al. Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020), its validity in the context of the present study is discussed in § 5.
2.1. Linear stability of the homogeneous and isotropic state
The Smoluchowski equation (2.2) and the normalisation condition (2.1) admit as a solution the homogeneous and isotropic state ![]() $\varPsi _{HI} = 1/( \varOmega _d V_d )$, where
$\varPsi _{HI} = 1/( \varOmega _d V_d )$, where ![]() $V_d$ is the
$V_d$ is the ![]() $d$-dimensional volume of the suspension. The existence of this solution relies on the condition
$d$-dimensional volume of the suspension. The existence of this solution relies on the condition
which is true in all cases considered in this work. Notice that, while integrals over ![]() $\boldsymbol {x}'$ and
$\boldsymbol {x}'$ and ![]() $\boldsymbol {p}'$ vanish independently in 2-D and 3-D bulk suspensions, only the positional integral vanishes for microswimmers restricted to a 2-D plane in a 3-D fluid.
$\boldsymbol {p}'$ vanish independently in 2-D and 3-D bulk suspensions, only the positional integral vanishes for microswimmers restricted to a 2-D plane in a 3-D fluid.
Stability of the homogeneous and isotropic state is determined by time evolution of small perturbations around ![]() $\varPsi _{HI}$. Techniques to study such problems are well established and have been extensively applied to linear stability analysis of the homogeneous and isotropic state for dilute 3-D suspensions of microswimmers (Saintillan & Shelley Reference Saintillan and Shelley2008a,Reference Saintillan and Shelleyb; Subramanian & Koch Reference Subramanian and Koch2009; Hohenegger & Shelley Reference Hohenegger and Shelley2010). Here, we use a somewhat different methodology (Stenhammar et al. Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017; Martinez et al. Reference Martinez2020), which is better adapted for our purpose.
$\varPsi _{HI}$. Techniques to study such problems are well established and have been extensively applied to linear stability analysis of the homogeneous and isotropic state for dilute 3-D suspensions of microswimmers (Saintillan & Shelley Reference Saintillan and Shelley2008a,Reference Saintillan and Shelleyb; Subramanian & Koch Reference Subramanian and Koch2009; Hohenegger & Shelley Reference Hohenegger and Shelley2010). Here, we use a somewhat different methodology (Stenhammar et al. Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017; Martinez et al. Reference Martinez2020), which is better adapted for our purpose.
First, we introduce a perturbation ![]() $\delta \varPsi (\boldsymbol {x},\boldsymbol {p},t)$ of the one-particle distribution function around the homogeneous and isotropic state, i.e.
$\delta \varPsi (\boldsymbol {x},\boldsymbol {p},t)$ of the one-particle distribution function around the homogeneous and isotropic state, i.e.
where we assume that ![]() $\delta \varPsi (\boldsymbol {x},\boldsymbol {p},t)$ is small and that its integral over
$\delta \varPsi (\boldsymbol {x},\boldsymbol {p},t)$ is small and that its integral over ![]() $\boldsymbol {x}$ and
$\boldsymbol {x}$ and ![]() $\boldsymbol {p}$ vanishes. In what follows, we employ the
$\boldsymbol {p}$ vanishes. In what follows, we employ the ![]() $d$-dimensional Fourier transform defined through
$d$-dimensional Fourier transform defined through
where ![]() $f$ is an arbitrary function of
$f$ is an arbitrary function of ![]() $\boldsymbol {x}$, and
$\boldsymbol {x}$, and ![]() $\hat f$ denotes its Fourier space representation. The linearised Smoluchowski (2.2) in Fourier space reads
$\hat f$ denotes its Fourier space representation. The linearised Smoluchowski (2.2) in Fourier space reads
where ![]() $n=N/V_d$ is the number density of particles, and we have defined the perturbations of the microswimmer density and fluid velocity as
$n=N/V_d$ is the number density of particles, and we have defined the perturbations of the microswimmer density and fluid velocity as
We proceed by assuming an exponential solution to (2.9) of the following form
where the sign of the real part of the temporal eigenvalue ![]() $\chi$ determines the stability of the system against infinitesimal perturbations: for Re
$\chi$ determines the stability of the system against infinitesimal perturbations: for Re![]() $[\chi ]<0$ the system is linearly stable, while for Re
$[\chi ]<0$ the system is linearly stable, while for Re![]() $[\chi ]>0$ the system is linearly unstable. It should be noted that a more general approach to the temporal linear stability analysis is to treat the problem as an initial value one and obtain the solution via the Laplace transformation, as was done in Stenhammar et al. (Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017) and Škultéty et al. (Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020). Working with the ansatz (2.12) is mathematically simpler but may not necessarily produce a dispersion law for all parameter values, as we discuss further below.
$[\chi ]>0$ the system is linearly unstable. It should be noted that a more general approach to the temporal linear stability analysis is to treat the problem as an initial value one and obtain the solution via the Laplace transformation, as was done in Stenhammar et al. (Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017) and Škultéty et al. (Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020). Working with the ansatz (2.12) is mathematically simpler but may not necessarily produce a dispersion law for all parameter values, as we discuss further below.
Inserting (2.12) into (2.9), we derive the following closed set of equations for the density and velocity perturbations:
where ![]() $\mathcal {L}(\chi,\boldsymbol {p}\boldsymbol {\cdot }\boldsymbol {k}) = \chi + \lambda + {\rm i} v_s \boldsymbol {p}\boldsymbol {\cdot }\boldsymbol {k}$. The solution to this eigenvalue problem depends on the precise form of the microscopic velocity field
$\mathcal {L}(\chi,\boldsymbol {p}\boldsymbol {\cdot }\boldsymbol {k}) = \chi + \lambda + {\rm i} v_s \boldsymbol {p}\boldsymbol {\cdot }\boldsymbol {k}$. The solution to this eigenvalue problem depends on the precise form of the microscopic velocity field ![]() $\hat {\boldsymbol {u}}(\boldsymbol {k},\boldsymbol {p})$, which, in turn, depends on the dimensionality of space and the dimensionality of the vectors
$\hat {\boldsymbol {u}}(\boldsymbol {k},\boldsymbol {p})$, which, in turn, depends on the dimensionality of space and the dimensionality of the vectors ![]() $\boldsymbol {p}$ and
$\boldsymbol {p}$ and ![]() $\boldsymbol {k}$. In the following, we begin by revisiting the known results on linear stability of bulk 3-D suspensions (Saintillan & Shelley Reference Saintillan and Shelley2008a,Reference Saintillan and Shelleyb) before turning our attention to a 2-D layer of microswimmers embedded in a 3-D fluid.
$\boldsymbol {k}$. In the following, we begin by revisiting the known results on linear stability of bulk 3-D suspensions (Saintillan & Shelley Reference Saintillan and Shelley2008a,Reference Saintillan and Shelleyb) before turning our attention to a 2-D layer of microswimmers embedded in a 3-D fluid.
3. Microswimmers in an unbounded bulk suspension
In this section, we consider the case of microswimmers that move freely in a 3-D space filled with an incompressible fluid. The dipolar velocity field for ![]() $d=3$ is given by (Lauga & Powers Reference Lauga and Powers2009)
$d=3$ is given by (Lauga & Powers Reference Lauga and Powers2009)
and, as shown in Appendix A, its Fourier transform is
Here, ![]() $\kappa$ is the dipolar strength and
$\kappa$ is the dipolar strength and ![]() $\mathbb {P}^{\alpha \beta } = \delta ^{\alpha \beta } - k^{\alpha } k^{\beta }/k^{2}$ is the transverse projection operator that ensures that (3.2) satisfies the incompressibility condition
$\mathbb {P}^{\alpha \beta } = \delta ^{\alpha \beta } - k^{\alpha } k^{\beta }/k^{2}$ is the transverse projection operator that ensures that (3.2) satisfies the incompressibility condition ![]() $k^\alpha \hat {u}_{3d}^\alpha = 0$. Setting
$k^\alpha \hat {u}_{3d}^\alpha = 0$. Setting ![]() $d = 3$ in (2.13)–(2.14), using the fact that
$d = 3$ in (2.13)–(2.14), using the fact that ![]() $\delta \hat {\mathcal {U}}^{\alpha } = \mathbb {P}^{\alpha \beta } \delta \hat {\mathcal {U}}^{\beta }$ and assuming that
$\delta \hat {\mathcal {U}}^{\alpha } = \mathbb {P}^{\alpha \beta } \delta \hat {\mathcal {U}}^{\beta }$ and assuming that ![]() $\chi$ does not depend on the orientation
$\chi$ does not depend on the orientation ![]() $\boldsymbol {p}$ (see further discussion below), we obtain the following set of equations: (Martinez et al. Reference Martinez2020)
$\boldsymbol {p}$ (see further discussion below), we obtain the following set of equations: (Martinez et al. Reference Martinez2020)
where we have introduced the dimensionless parameter
We note that (3.3) and (3.4) are decoupled, and can be studied independently. The former equation involves only ![]() $\delta \hat {\rho }$, and we thus refer to it as the density eigenvalue problem. The latter equation is known to lead to a long-wavelength instability associated with orientational degrees of freedom only (Saintillan & Shelley Reference Saintillan and Shelley2008a,Reference Saintillan and Shelleyb; Subramanian & Koch Reference Subramanian and Koch2009; Hohenegger & Shelley Reference Hohenegger and Shelley2010; Stenhammar et al. Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017), and we thus refer to it as the orientational eigenvalue problem. We will now study these two problems separately, while the analogous calculation for the case of an infinite 2-D suspension is carried out in Appendix B with qualitatively identical conclusions.
$\delta \hat {\rho }$, and we thus refer to it as the density eigenvalue problem. The latter equation is known to lead to a long-wavelength instability associated with orientational degrees of freedom only (Saintillan & Shelley Reference Saintillan and Shelley2008a,Reference Saintillan and Shelleyb; Subramanian & Koch Reference Subramanian and Koch2009; Hohenegger & Shelley Reference Hohenegger and Shelley2010; Stenhammar et al. Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017), and we thus refer to it as the orientational eigenvalue problem. We will now study these two problems separately, while the analogous calculation for the case of an infinite 2-D suspension is carried out in Appendix B with qualitatively identical conclusions.
3.1. Bulk orientational instability
Equation (3.4) yields the following eigenvalue problem:
We now solve (3.5) for ![]() $\chi$ and use the definition of
$\chi$ and use the definition of ![]() $\gamma$ from (3.6), to arrive at
$\gamma$ from (3.6), to arrive at
Equation (3.6) can be inverted numerically to obtain ![]() $b(\gamma )$ or, equivalently,
$b(\gamma )$ or, equivalently, ![]() $F(\gamma )$, while an analytical approximation to
$F(\gamma )$, while an analytical approximation to ![]() $F(\gamma )$ was developed in Škultéty et al. (Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020) and Martinez et al. (Reference Martinez2020). In figure 2 we plot the results of our numerical evaluation of
$F(\gamma )$ was developed in Škultéty et al. (Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020) and Martinez et al. (Reference Martinez2020). In figure 2 we plot the results of our numerical evaluation of ![]() $F(\gamma )$, showing that (i) the real part of
$F(\gamma )$, showing that (i) the real part of ![]() $F$ is positive and decreases monotonically with increasing
$F$ is positive and decreases monotonically with increasing ![]() $\gamma$, and (ii) no solution is found for
$\gamma$, and (ii) no solution is found for ![]() $\gamma >\gamma ^*$, a fact that is discussed further below. Together with (3.7), this implies that puller suspensions (
$\gamma >\gamma ^*$, a fact that is discussed further below. Together with (3.7), this implies that puller suspensions (![]() $\kappa < 0$) are always stable while the instability of pusher suspensions (
$\kappa < 0$) are always stable while the instability of pusher suspensions (![]() $\kappa > 0$) sets in at the largest possible length scale, corresponding to
$\kappa > 0$) sets in at the largest possible length scale, corresponding to ![]() $\gamma \rightarrow 0$ and
$\gamma \rightarrow 0$ and ![]() $F(\gamma ) \rightarrow 1$. It follows from (3.7), and from imposing
$F(\gamma ) \rightarrow 1$. It follows from (3.7), and from imposing ![]() $\chi >0$, that pusher suspensions are unstable for densities larger than
$\chi >0$, that pusher suspensions are unstable for densities larger than
This latter result is exact, and can be alternatively derived directly from (3.4) by setting ![]() $k \rightarrow 0$.
$k \rightarrow 0$.

Figure 2. The real (a) and imaginary (b) parts of the function ![]() $F(\gamma )$ from (3.7).
$F(\gamma )$ from (3.7).
The origin of this instability is the mutual reorientation of microswimmers (Saintillan & Shelley Reference Saintillan and Shelley2008a,Reference Saintillan and Shelleyb; Subramanian & Koch Reference Subramanian and Koch2009; Hohenegger & Shelley Reference Hohenegger and Shelley2010; Stenhammar et al. Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017). It is thus unsurprising to observe that no instability is present for spherical particles (![]() $B=0$). Furthermore, the instability condition (3.8) does not involve the swimming speed
$B=0$). Furthermore, the instability condition (3.8) does not involve the swimming speed ![]() $v_s$, implying that the orientational instability persists even for shakers – microswimmers that do not self-propel, yet are capable of generating dipolar fields (Stenhammar et al. Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017).
$v_s$, implying that the orientational instability persists even for shakers – microswimmers that do not self-propel, yet are capable of generating dipolar fields (Stenhammar et al. Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017).
We finally comment on the fact that no solution for ![]() $F(\gamma )$ is found for
$F(\gamma )$ is found for ![]() $\gamma >\gamma ^*\approx 2.8$. This means that a solution to the linearised kinetic equation (2.9) obeying the ansatz (2.12) ceases to exist for
$\gamma >\gamma ^*\approx 2.8$. This means that a solution to the linearised kinetic equation (2.9) obeying the ansatz (2.12) ceases to exist for ![]() $\gamma >\gamma ^*$. The reason for this is that, in the process of deriving (3.3)–(3.4), we have assumed that
$\gamma >\gamma ^*$. The reason for this is that, in the process of deriving (3.3)–(3.4), we have assumed that ![]() $\chi$ is independent of the swimmer orientation
$\chi$ is independent of the swimmer orientation ![]() $\boldsymbol {p}$. Hohenegger & Shelley (Reference Hohenegger and Shelley2010) performed a detailed analysis of the eigenvalue problem in this parameter range avoiding such an assumption, and concluded that the system is linearly stable for
$\boldsymbol {p}$. Hohenegger & Shelley (Reference Hohenegger and Shelley2010) performed a detailed analysis of the eigenvalue problem in this parameter range avoiding such an assumption, and concluded that the system is linearly stable for ![]() $\gamma > \gamma ^{*}$. The most unstable eigenvalue is thus given by (3.7), leading to the instability threshold (3.8). The same conclusion is reached by solving (2.9) using Laplace transform techniques, as was done in Stenhammar et al. (Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017) and Škultéty et al. (Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020).
$\gamma > \gamma ^{*}$. The most unstable eigenvalue is thus given by (3.7), leading to the instability threshold (3.8). The same conclusion is reached by solving (2.9) using Laplace transform techniques, as was done in Stenhammar et al. (Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017) and Škultéty et al. (Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020).
3.2. Density fluctuations in bulk suspensions
Both puller and pusher suspensions are stable against density fluctuations. For wavenumbers ![]() $k \leq {\rm \pi}\lambda /(2v_{s})$ this can be readily shown from (3.3), yielding
$k \leq {\rm \pi}\lambda /(2v_{s})$ this can be readily shown from (3.3), yielding
from which we conclude that ![]() $\chi <0$. The corresponding eigenstates represent spatial modulation of the microswimmer density, while their orientations remain isotropically distributed regardless of their spatial positions. Similar to the orientational instability, (3.3) does not allow one to determine stability of the suspension when
$\chi <0$. The corresponding eigenstates represent spatial modulation of the microswimmer density, while their orientations remain isotropically distributed regardless of their spatial positions. Similar to the orientational instability, (3.3) does not allow one to determine stability of the suspension when ![]() $k > {\rm \pi}\lambda /(2v_{s})$, since, in this regime, (3.3) has no solution. As discussed in § 3.1, this is a limitation of the ansatz (2.12). In Appendix C.1, we analyse this problem in some detail by solving (2.9) using Laplace transform techniques and show that the system is indeed stable with respect to infinitesimal density perturbations for all
$k > {\rm \pi}\lambda /(2v_{s})$, since, in this regime, (3.3) has no solution. As discussed in § 3.1, this is a limitation of the ansatz (2.12). In Appendix C.1, we analyse this problem in some detail by solving (2.9) using Laplace transform techniques and show that the system is indeed stable with respect to infinitesimal density perturbations for all ![]() $k$.
$k$.
4. Microswimmers restricted to a 2-D plane
We now turn our attention to the main problem of this study – the case of a 2-D layer of microswimmers embedded in a 3-D bulk fluid. As discussed in § 1, this spatial arrangement of microswimmers leads to the in-plane fluid velocity field being effectively compressible, with pushers acting on average as sources, while pullers act as sinks. Here, we study the consequences of this effective compressibility on the onset and type of collective motion expected in this arrangement of microswimmers.
The Fourier representation of the in-plane velocity field created by a microswimmer is given by (see Appendix A for details)
 \begin{equation} u_{plane}^{\alpha}(\boldsymbol{\mathcal{k}},\boldsymbol{\mathcal{p}}) ={-} \frac{{\rm i}\kappa}{2} \frac{\boldsymbol{\mathcal{k}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}}}{\mathcal{k}} \left[ \mathbb{P}^{\alpha\beta} + \frac{1}{2} \mathbb{Q}^{\alpha\beta} \right] \mathcal{p}^{\beta}, \end{equation}
\begin{equation} u_{plane}^{\alpha}(\boldsymbol{\mathcal{k}},\boldsymbol{\mathcal{p}}) ={-} \frac{{\rm i}\kappa}{2} \frac{\boldsymbol{\mathcal{k}}\boldsymbol{\cdot}\boldsymbol{\mathcal{p}}}{\mathcal{k}} \left[ \mathbb{P}^{\alpha\beta} + \frac{1}{2} \mathbb{Q}^{\alpha\beta} \right] \mathcal{p}^{\beta}, \end{equation}
where ![]() $\kappa$ is the dipolar strength which has the same dimensions as in the bulk 3-D case, and
$\kappa$ is the dipolar strength which has the same dimensions as in the bulk 3-D case, and ![]() $\boldsymbol {\mathcal {k}} = ( \mathcal {k}_x, \mathcal {k}_y)$,
$\boldsymbol {\mathcal {k}} = ( \mathcal {k}_x, \mathcal {k}_y)$, ![]() $\boldsymbol {\mathcal {p}} = ( \mathcal {p}_x, \mathcal {p}_y)$ are respectively the in-plane wave and orientation vectors. In writing (4.1), we explicitly separated the term proportional to the longitudinal projection operator
$\boldsymbol {\mathcal {p}} = ( \mathcal {p}_x, \mathcal {p}_y)$ are respectively the in-plane wave and orientation vectors. In writing (4.1), we explicitly separated the term proportional to the longitudinal projection operator ![]() $\mathbb {Q}^{\alpha \beta } = \mathcal {k}^{\alpha } \mathcal {k}^{\beta } / \mathcal {k}^{2}$ to stress the compressible nature of
$\mathbb {Q}^{\alpha \beta } = \mathcal {k}^{\alpha } \mathcal {k}^{\beta } / \mathcal {k}^{2}$ to stress the compressible nature of ![]() $\boldsymbol {u}_{plane}$. We now define the transverse (incompressible) and longitudinal (compressible) velocity perturbations by
$\boldsymbol {u}_{plane}$. We now define the transverse (incompressible) and longitudinal (compressible) velocity perturbations by
where ![]() $\delta \hat {\mathcal {U}}^{\alpha } = \delta \hat {\mathcal {U}}_{\perp }^{\alpha } + \delta \hat {\mathcal {U}}_{\parallel }^{\alpha }$. Substituting (4.1) for
$\delta \hat {\mathcal {U}}^{\alpha } = \delta \hat {\mathcal {U}}_{\perp }^{\alpha } + \delta \hat {\mathcal {U}}_{\parallel }^{\alpha }$. Substituting (4.1) for ![]() $\boldsymbol {u}_{plane}$ into (2.13)–(2.14) results in the following compact set of equations determining linear stability of the system:
$\boldsymbol {u}_{plane}$ into (2.13)–(2.14) results in the following compact set of equations determining linear stability of the system:
 \begin{equation} \begin{pmatrix} M_{11}-1 & 0 & 0 \\ 0 & M_{22}-1 & {\rm i} \mathcal{k}^{\alpha} M_{23} \\ 0 & {\rm i} \mathcal{k}^{\alpha} M_{32} & M_{33}-1 \end{pmatrix} {\cdot} \begin{pmatrix} \delta \hat{\mathcal{U}}_{{\perp}}^{\alpha} \\ \delta \hat{\mathcal{U}}_{{\parallel}}^{\alpha} \\ \delta \hat{\rho} \end{pmatrix} = 0, \end{equation}
\begin{equation} \begin{pmatrix} M_{11}-1 & 0 & 0 \\ 0 & M_{22}-1 & {\rm i} \mathcal{k}^{\alpha} M_{23} \\ 0 & {\rm i} \mathcal{k}^{\alpha} M_{32} & M_{33}-1 \end{pmatrix} {\cdot} \begin{pmatrix} \delta \hat{\mathcal{U}}_{{\perp}}^{\alpha} \\ \delta \hat{\mathcal{U}}_{{\parallel}}^{\alpha} \\ \delta \hat{\rho} \end{pmatrix} = 0, \end{equation}where
 \begin{equation} \left. \begin{gathered} M_{11} = \frac{\kappa n}{v_{s}} \frac{B \left(b^2-2 \sqrt{b^2+1}+2\right) }{2 b^3}, \quad M_{22} = \frac{\kappa n}{v_{s}} \frac{B b^2 + (b^{2} + 2B)\left( 1 - \sqrt{b^{2} + 1} \right)}{4 b^3 \sqrt{b^2+1}}, \\ M_{23} = \frac{\kappa\lambda}{ v_{s} \mathcal{k}^{2} } \frac{1}{4 b} \left( \frac{1}{\sqrt{b^2+1}}-1 \right) , \quad M_{32} = \frac{n}{ v_{s} \mathcal{k}} \frac{2 B \left(\sqrt{b^2+1}-1\right) -b^2 (B+1)}{b \sqrt{b^2+1}} , \\ M_{33} = \frac{\lambda}{\mathcal{k} v_{s}} \frac{b}{\sqrt{1+b^{2}}}, \end{gathered} \right\} \end{equation}
\begin{equation} \left. \begin{gathered} M_{11} = \frac{\kappa n}{v_{s}} \frac{B \left(b^2-2 \sqrt{b^2+1}+2\right) }{2 b^3}, \quad M_{22} = \frac{\kappa n}{v_{s}} \frac{B b^2 + (b^{2} + 2B)\left( 1 - \sqrt{b^{2} + 1} \right)}{4 b^3 \sqrt{b^2+1}}, \\ M_{23} = \frac{\kappa\lambda}{ v_{s} \mathcal{k}^{2} } \frac{1}{4 b} \left( \frac{1}{\sqrt{b^2+1}}-1 \right) , \quad M_{32} = \frac{n}{ v_{s} \mathcal{k}} \frac{2 B \left(\sqrt{b^2+1}-1\right) -b^2 (B+1)}{b \sqrt{b^2+1}} , \\ M_{33} = \frac{\lambda}{\mathcal{k} v_{s}} \frac{b}{\sqrt{1+b^{2}}}, \end{gathered} \right\} \end{equation}and
As is apparent from (4.3), ![]() $\delta \hat {\mathcal {U}}_{\perp }^{\alpha }$ is decoupled from
$\delta \hat {\mathcal {U}}_{\perp }^{\alpha }$ is decoupled from ![]() $\delta \hat {\mathcal {U}}_{\parallel }^{\alpha }$ and
$\delta \hat {\mathcal {U}}_{\parallel }^{\alpha }$ and ![]() $\delta \hat {\rho }$. This allows us to analyse the two subsets of equations independently; as we show below, they correspond to different types of instabilities.
$\delta \hat {\rho }$. This allows us to analyse the two subsets of equations independently; as we show below, they correspond to different types of instabilities.
4.1. Orientational instability
We start by considering the transverse mode ![]() $\delta \mathcal {U}_{\perp }^{\alpha }$, which amounts to solving
$\delta \mathcal {U}_{\perp }^{\alpha }$, which amounts to solving ![]() $M_{11} = 1$. This yields
$M_{11} = 1$. This yields
Assuming that ![]() $b \neq 0$, (4.6) can be transformed into a polynomial equation that can be solved analytically. Inserting the obtained roots into (4.6), we found that only two solutions to (4.6) exist, and only within the region
$b \neq 0$, (4.6) can be transformed into a polynomial equation that can be solved analytically. Inserting the obtained roots into (4.6), we found that only two solutions to (4.6) exist, and only within the region ![]() $2\sqrt {2}v_{s} \le B \kappa n$. In analogy with (3.6) for the bulk suspension, the eigenvalue
$2\sqrt {2}v_{s} \le B \kappa n$. In analogy with (3.6) for the bulk suspension, the eigenvalue ![]() $\chi$ within this parameter range is found to have the following form:
$\chi$ within this parameter range is found to have the following form:
where
 \begin{gather} G(x) = 6x^{2} \left( 4 - \frac{\left(1\pm {\rm i} \sqrt{3}\right)}{ H(x)} - \left(1\mp {\rm i} \sqrt{3}\right) H(x) \right)^{{-}1}, \end{gather}
\begin{gather} G(x) = 6x^{2} \left( 4 - \frac{\left(1\pm {\rm i} \sqrt{3}\right)}{ H(x)} - \left(1\mp {\rm i} \sqrt{3}\right) H(x) \right)^{{-}1}, \end{gather}
Similar to the bulk suspension, in the region ![]() $2\sqrt {2} v_{s} > B \kappa n$, where the solution to (4.6) does not exist, stability analysis requires the use of an alternative approach. This is discussed in Appendix C.2, where we show that the system remains stable in this parameter range.
$2\sqrt {2} v_{s} > B \kappa n$, where the solution to (4.6) does not exist, stability analysis requires the use of an alternative approach. This is discussed in Appendix C.2, where we show that the system remains stable in this parameter range.
The function ![]() $G$ has the same qualitative features as the function
$G$ has the same qualitative features as the function ![]() $F$ in the case of bulk suspensions (compare figures 2 and 5 (see Appendix B)): its real part is positive and its largest branch is a monotonically decreasing function of its argument. Because (4.7) is an increasing function of
$F$ in the case of bulk suspensions (compare figures 2 and 5 (see Appendix B)): its real part is positive and its largest branch is a monotonically decreasing function of its argument. Because (4.7) is an increasing function of ![]() $\mathcal {k}$, the orientational instability in a 2-D layer of microswimmers embedded in a 3-D fluid sets in at the largest possible value of
$\mathcal {k}$, the orientational instability in a 2-D layer of microswimmers embedded in a 3-D fluid sets in at the largest possible value of ![]() $\mathcal {k}$, in contrast with bulk pusher suspensions. In the absence of any physical restrictions on the maximum value taken by
$\mathcal {k}$, in contrast with bulk pusher suspensions. In the absence of any physical restrictions on the maximum value taken by ![]() $\mathcal {k}$, this instability occurs for
$\mathcal {k}$, this instability occurs for
Just as in bulk systems, the fact that ![]() $n_{c}$ diverges for spherical particles (
$n_{c}$ diverges for spherical particles (![]() $B=0$) shows that this is an instability driven by particle reorientations due to hydrodynamic interactions. However, unlike the 3-D bulk case (3.8),
$B=0$) shows that this is an instability driven by particle reorientations due to hydrodynamic interactions. However, unlike the 3-D bulk case (3.8), ![]() $n_c$ is now a function of the swimming speed
$n_c$ is now a function of the swimming speed ![]() $v_s$ rather than of the tumbling rate
$v_s$ rather than of the tumbling rate ![]() $\lambda$, meaning that increasing the swimming speed will stabilise a sheet of pushers, which become unstable for any density in the shaker limit
$\lambda$, meaning that increasing the swimming speed will stabilise a sheet of pushers, which become unstable for any density in the shaker limit ![]() $v_s \to 0$. While the stabilising role of swimming in the stability and pre-transitional correlations of finite microswimmer systems has previously been discussed for 3-D bulk suspensions (Saintillan & Shelley Reference Saintillan and Shelley2013; Liu, Zhang & Cheng Reference Liu, Zhang and Cheng2019; Škultéty et al. Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020; Martinez et al. Reference Martinez2020; Albritton & Ohm Reference Albritton and Ohm2023), its effect on the stability of a sheet of pusher microswimmers, (4.10), is significantly stronger. Finally, the independence of
$v_s \to 0$. While the stabilising role of swimming in the stability and pre-transitional correlations of finite microswimmer systems has previously been discussed for 3-D bulk suspensions (Saintillan & Shelley Reference Saintillan and Shelley2013; Liu, Zhang & Cheng Reference Liu, Zhang and Cheng2019; Škultéty et al. Reference Škultéty, Nardini, Stenhammar, Marenduzzo and Morozov2020; Martinez et al. Reference Martinez2020; Albritton & Ohm Reference Albritton and Ohm2023), its effect on the stability of a sheet of pusher microswimmers, (4.10), is significantly stronger. Finally, the independence of ![]() $n_{c}$ of the tumbling rate implies that even a suspension of straight swimmers has a non-vanishing critical density, in contrast to the case encountered in 3-D bulk suspensions.
$n_{c}$ of the tumbling rate implies that even a suspension of straight swimmers has a non-vanishing critical density, in contrast to the case encountered in 3-D bulk suspensions.
The above reasoning for deriving the orientational instability assumes that the most unstable wave vector is ![]() $\mathcal {k}_c \to \infty$; this is clearly unphysical since it corresponds to microscopic length scales. In practice, the instability instead sets in at some finite length scale
$\mathcal {k}_c \to \infty$; this is clearly unphysical since it corresponds to microscopic length scales. In practice, the instability instead sets in at some finite length scale ![]() $l_c$, corresponding to a finite value of
$l_c$, corresponding to a finite value of ![]() $\mathcal {k}_c$. As observed previously for 3-D bulk suspensions (Saintillan & Shelley Reference Saintillan and Shelley2008a; Subramanian & Koch Reference Subramanian and Koch2009), one possible source of regularisation is provided by the spatial diffusivity of microswimmers. Repeating the above analysis in the presence of Brownian diffusion yields an additional term,
$\mathcal {k}_c$. As observed previously for 3-D bulk suspensions (Saintillan & Shelley Reference Saintillan and Shelley2008a; Subramanian & Koch Reference Subramanian and Koch2009), one possible source of regularisation is provided by the spatial diffusivity of microswimmers. Repeating the above analysis in the presence of Brownian diffusion yields an additional term, ![]() $-D\mathcal {k}^2$, on the right-hand side of (4.7), where
$-D\mathcal {k}^2$, on the right-hand side of (4.7), where ![]() $D$ is the diffusion constant. Minimising the real part of the eigenvalue with respect to
$D$ is the diffusion constant. Minimising the real part of the eigenvalue with respect to ![]() $k$ leads to the length scale
$k$ leads to the length scale ![]() $l_c \sim \sqrt {D/\lambda }$ being selected at the instability. Using the approximate values
$l_c \sim \sqrt {D/\lambda }$ being selected at the instability. Using the approximate values ![]() $D\sim 0.2- 0.4\ \mathrm {\mu }\textrm {m}^2\ \textrm {s}^{-1}$ (Jepson et al. Reference Jepson, Martinez, Schwarz-Linek, Morozov and Poon2013) and
$D\sim 0.2- 0.4\ \mathrm {\mu }\textrm {m}^2\ \textrm {s}^{-1}$ (Jepson et al. Reference Jepson, Martinez, Schwarz-Linek, Morozov and Poon2013) and ![]() $\lambda \sim 1\ \textrm {s}^{-1}$, this length scale becomes comparable to the microswimmer size,
$\lambda \sim 1\ \textrm {s}^{-1}$, this length scale becomes comparable to the microswimmer size, ![]() $l_c \sim 1\ \mathrm {\mu }\textrm {m}$, which is an unphysically small length scale for the instability to occur. It is therefore unlikely that spatial diffusivity is the relevant mechanism of the length scale selection in (4.7).
$l_c \sim 1\ \mathrm {\mu }\textrm {m}$, which is an unphysically small length scale for the instability to occur. It is therefore unlikely that spatial diffusivity is the relevant mechanism of the length scale selection in (4.7).
The second relevant microscopic length scale in the problem is the (density-dependent) average distance between microswimmers, below which the system can no longer be viewed as a continuum. Thus, we assume that the length scale selected at the instability is now ![]() $l_c \sim 2/\sqrt {{\rm \pi} n_c}$, leading to a maximum wave vector
$l_c \sim 2/\sqrt {{\rm \pi} n_c}$, leading to a maximum wave vector
The calculation of the corresponding instability threshold is outlined in Appendix D, leading to the following approximate expression for ![]() $n_c$:
$n_c$:
 \begin{equation} n_{c} \approx \frac{4}{\rm \pi} \left( \frac{\lambda}{B\kappa} \right)^{2/3} + 2\sqrt{2} \frac{v_{s}}{B\kappa}. \end{equation}
\begin{equation} n_{c} \approx \frac{4}{\rm \pi} \left( \frac{\lambda}{B\kappa} \right)^{2/3} + 2\sqrt{2} \frac{v_{s}}{B\kappa}. \end{equation}
We observe that the critical density (4.12) differs from its ![]() $\mathcal {k}_c \to \infty$ counterpart (4.10) by the presence of the first term, which dominates at low swimming speeds. Using the experimental values
$\mathcal {k}_c \to \infty$ counterpart (4.10) by the presence of the first term, which dominates at low swimming speeds. Using the experimental values ![]() $v_s \approx 15\ \mathrm {\mu }\textrm {m}\ \textrm {s}^{-1}$,
$v_s \approx 15\ \mathrm {\mu }\textrm {m}\ \textrm {s}^{-1}$, ![]() $\kappa \approx 800\ \mathrm {\mu }\textrm {m}^3\ \textrm {s}^{-1}$ measured in Drescher et al. (Reference Drescher, Dunkel, Cisneros, Ganguly and Goldstein2011), together with
$\kappa \approx 800\ \mathrm {\mu }\textrm {m}^3\ \textrm {s}^{-1}$ measured in Drescher et al. (Reference Drescher, Dunkel, Cisneros, Ganguly and Goldstein2011), together with ![]() $B \approx 1$ and
$B \approx 1$ and ![]() $\lambda \approx 1\ \textrm {s}^{-1}$, (4.12) and (4.11) give the critical length scale
$\lambda \approx 1\ \textrm {s}^{-1}$, (4.12) and (4.11) give the critical length scale ![]() $l_c\sim 4$
$l_c\sim 4$ ![]() $\mathrm {\mu }$m, which is larger than, although comparable to, the value resulting from translational diffusion.
$\mathrm {\mu }$m, which is larger than, although comparable to, the value resulting from translational diffusion.
4.2. Density instability
The second subset of (4.4) couples ![]() $\delta \hat {\mathcal {U}}_{\parallel }^{\alpha }$ and
$\delta \hat {\mathcal {U}}_{\parallel }^{\alpha }$ and ![]() $\delta \hat {\rho }$ and thus governs the appearance of density modulations within the microswimmer layer. After some algebra, this set of equations can be re-expressed as
$\delta \hat {\rho }$ and thus governs the appearance of density modulations within the microswimmer layer. After some algebra, this set of equations can be re-expressed as
 \begin{equation} \frac{\varPhi \tilde{\mathcal{k}} \left[ B \left(b^2 + 2- 2 \sqrt{b^2+1}\right) y - b^2 \left(\sqrt{b^2+1}-1\right) (y+1) \right]}{4 b^4 (y+1) \left[ \sqrt{b^2+1}(y + 1)-1 \right]} = 1, \end{equation}
\begin{equation} \frac{\varPhi \tilde{\mathcal{k}} \left[ B \left(b^2 + 2- 2 \sqrt{b^2+1}\right) y - b^2 \left(\sqrt{b^2+1}-1\right) (y+1) \right]}{4 b^4 (y+1) \left[ \sqrt{b^2+1}(y + 1)-1 \right]} = 1, \end{equation}where we have introduced the following dimensionless quantities:
A full analytical solution of (4.13) cannot be found, but can be achieved perturbatively for small ![]() $\tilde {\mathcal {k}}$, yielding
$\tilde {\mathcal {k}}$, yielding
From this expression, we conclude that (i) pusher suspensions (![]() $\varPhi >0$) are stable against density modulations at large spatial scales since
$\varPhi >0$) are stable against density modulations at large spatial scales since ![]() $y < 0$ for small
$y < 0$ for small ![]() $\tilde {\mathcal {k}}$, and (ii) puller suspensions (
$\tilde {\mathcal {k}}$, and (ii) puller suspensions (![]() $\varPhi < 0$) are linearly unstable at any density. Note that this instability is independent of
$\varPhi < 0$) are linearly unstable at any density. Note that this instability is independent of ![]() $B$, and hence occurs even for spherical particles. Even though the puller density instability occurs at vanishingly small densities in an infinite system, for a finite system with linear size
$B$, and hence occurs even for spherical particles. Even though the puller density instability occurs at vanishingly small densities in an infinite system, for a finite system with linear size ![]() $H$ one can show that puller suspensions are unstable against large-scale perturbations only above a critical density
$H$ one can show that puller suspensions are unstable against large-scale perturbations only above a critical density ![]() $n_c$ given by
$n_c$ given by
This result is obtained by assuming that the eigenvalue ![]() $y$ is real for small
$y$ is real for small ![]() $\tilde {\mathcal {k}}$, setting
$\tilde {\mathcal {k}}$, setting ![]() $y = 0$ in (4.13), and assuming that the critical wave vector
$y = 0$ in (4.13), and assuming that the critical wave vector ![]() $\mathcal {k}_c$ is set by the system dimensions, i.e.
$\mathcal {k}_c$ is set by the system dimensions, i.e. ![]() $\mathcal {k}_c = 2{\rm \pi} /H$.
$\mathcal {k}_c = 2{\rm \pi} /H$.
We now proceed by solving (4.13) numerically, which we have done for several values of ![]() $B$ and
$B$ and ![]() $\varPhi$, as shown in figure 3. This analysis indeed confirms both the existence of a finite-wavelength instability in puller suspensions at large spatial scales (small
$\varPhi$, as shown in figure 3. This analysis indeed confirms both the existence of a finite-wavelength instability in puller suspensions at large spatial scales (small ![]() $\mathcal {k}$), and that a sheet of pushers is always stable against density perturbations. However, it also shows that, when
$\mathcal {k}$), and that a sheet of pushers is always stable against density perturbations. However, it also shows that, when ![]() $\varPhi$ is sufficiently negative,
$\varPhi$ is sufficiently negative, ![]() $\mathrm {Re}[y]$ increases in an unbounded fashion at large
$\mathrm {Re}[y]$ increases in an unbounded fashion at large ![]() $\mathcal {k}$ for pullers. Thus, a second density instability, now at small spatial scales, emerges in puller suspensions for sufficiently large densities. To analyse this effect further, we numerically calculate the largest eigenvalue from (4.13). The resulting phase diagram is shown in figure 4, which displays the critical scale
$\mathcal {k}$ for pullers. Thus, a second density instability, now at small spatial scales, emerges in puller suspensions for sufficiently large densities. To analyse this effect further, we numerically calculate the largest eigenvalue from (4.13). The resulting phase diagram is shown in figure 4, which displays the critical scale ![]() $\mathcal {k}_c$ as a function of the dimensionless system size
$\mathcal {k}_c$ as a function of the dimensionless system size ![]() $H \lambda /v_s$ and the reduced particle density
$H \lambda /v_s$ and the reduced particle density ![]() $\varPhi$. Our findings confirm that the density instability in the confined suspension sets in either at the smallest or the largest available spatial scale, depending on the system parameters as encoded in
$\varPhi$. Our findings confirm that the density instability in the confined suspension sets in either at the smallest or the largest available spatial scale, depending on the system parameters as encoded in ![]() $\varPhi$ and
$\varPhi$ and ![]() $B$. In drawing the phase diagram we have, in analogy to § 4.1, chosen a cutoff at small scales corresponding to the interparticle separation (i.e.
$B$. In drawing the phase diagram we have, in analogy to § 4.1, chosen a cutoff at small scales corresponding to the interparticle separation (i.e. ![]() $\mathcal {k} = \sqrt { {\rm \pi}^{3} n }$ ). In the dimensionless units used here, the maximal wavenumber available is set by
$\mathcal {k} = \sqrt { {\rm \pi}^{3} n }$ ). In the dimensionless units used here, the maximal wavenumber available is set by ![]() $\tilde {\mathcal {k}}=\sqrt {{\rm \pi} ^3 \varPhi } \sqrt {v_s^3/\lambda ^2 \kappa }$, where the factor
$\tilde {\mathcal {k}}=\sqrt {{\rm \pi} ^3 \varPhi } \sqrt {v_s^3/\lambda ^2 \kappa }$, where the factor ![]() $\sqrt {v_s^3/\lambda ^2 \kappa } \sim \mathcal {O}(1)$ for free-swimming E. coli bacteria (Drescher et al. Reference Drescher, Dunkel, Cisneros, Ganguly and Goldstein2011).
$\sqrt {v_s^3/\lambda ^2 \kappa } \sim \mathcal {O}(1)$ for free-swimming E. coli bacteria (Drescher et al. Reference Drescher, Dunkel, Cisneros, Ganguly and Goldstein2011).

Figure 3. The real (a) and imaginary (b) parts of the eigenvalue ![]() $y = \chi /\lambda$ corresponding to density perturbations, obtained by numerically solving (4.13). All plots correspond to needle-like particles (
$y = \chi /\lambda$ corresponding to density perturbations, obtained by numerically solving (4.13). All plots correspond to needle-like particles (![]() $B = 1$), but are qualitatively similar for all values of
$B = 1$), but are qualitatively similar for all values of ![]() $B$. For pushers (
$B$. For pushers (![]() $\varPhi > 0$), the real part of the eigenvalue is strictly negative. For pullers (
$\varPhi > 0$), the real part of the eigenvalue is strictly negative. For pullers (![]() $\varPhi < 0$), the real part of the eigenvalue becomes positive at small wave vectors. At larger densities, the global maximum of
$\varPhi < 0$), the real part of the eigenvalue becomes positive at small wave vectors. At larger densities, the global maximum of ![]() $\mathrm {Re} [y]$ moves from small
$\mathrm {Re} [y]$ moves from small ![]() $\tilde {\mathcal {k}}$ to
$\tilde {\mathcal {k}}$ to ![]() $\tilde {\mathcal {k}} \to \infty$. No solution exists in the region Re
$\tilde {\mathcal {k}} \to \infty$. No solution exists in the region Re![]() $[y] < - 1$, whose stability is instead addressed in Appendix C.1.
$[y] < - 1$, whose stability is instead addressed in Appendix C.1.

Figure 4. Density instability in a 2-D puller suspension embedded in a 3-D fluid. The phase diagrams show regions of the two types of density instability obtained by numerical solution of (4.13). At high ![]() $\varPhi$ (grey regions), the instability sets in at the smallest physically relevant spatial scale, which we assume to be the particle–particle separation, i.e.
$\varPhi$ (grey regions), the instability sets in at the smallest physically relevant spatial scale, which we assume to be the particle–particle separation, i.e. ![]() $\tilde {\mathcal {k}}=\sqrt {{\rm \pi} ^3 \varPhi } \sqrt {v_s^3/\lambda ^2 \kappa }$, and set
$\tilde {\mathcal {k}}=\sqrt {{\rm \pi} ^3 \varPhi } \sqrt {v_s^3/\lambda ^2 \kappa }$, and set ![]() $\sqrt {v_s^3/\lambda ^2 \kappa }=1$. At moderate and low
$\sqrt {v_s^3/\lambda ^2 \kappa }=1$. At moderate and low ![]() $\varPhi$ (red heat map), the instability sets in at larger spatial scales set by the maximum of the arc-like part of the dispersion law; see figure 3. If the system size
$\varPhi$ (red heat map), the instability sets in at larger spatial scales set by the maximum of the arc-like part of the dispersion law; see figure 3. If the system size ![]() $H$ is too small, the latter maximum in the dispersion law cannot be accessed, and the instability instead sets in at the scale of the system dimensions. (a)
$H$ is too small, the latter maximum in the dispersion law cannot be accessed, and the instability instead sets in at the scale of the system dimensions. (a) ![]() $B = 1$, (b)
$B = 1$, (b) ![]() $B = 0$.
$B = 0$.
These results show that, while the density instability is present also for spherical particles, the particle shape strongly affects the emergence of small- and large-scale instabilities in that the small-scale instability dominates over a wider range of ![]() $\varPhi$ values compared with the elongated (
$\varPhi$ values compared with the elongated (![]() $B=1$) particle case. Understanding the physical manifestations of these two instabilities requires detailed investigations using explicit numerical simulations and is left for future work.
$B=1$) particle case. Understanding the physical manifestations of these two instabilities requires detailed investigations using explicit numerical simulations and is left for future work.
5. Conclusion
In this work, we have analysed the linear stability of the homogeneous and isotropic distribution of microswimmers restricted to a 2-D plane embedded in a 3-D bulk viscous fluid. Our method, based on mean-field kinetic theory, is somewhat different from that used in the previous analysis of bulk suspensions (Saintillan & Shelley Reference Saintillan and Shelley2008a,Reference Saintillan and Shelleyb; Subramanian & Koch Reference Subramanian and Koch2009; Hohenegger & Shelley Reference Hohenegger and Shelley2010) and allows us to easily identify the origin of the instability as either an orientational mode, stemming from the mutual reorientation of microswimmers, or a density mode, stemming from local accumulation of microswimmers.
The instabilities we found for a sheet of microswimmers are qualitatively different from their bulk counterpart. In such infinite 2-D or 3-D systems, linear stability analysis shows the presence of an orientational instability for pushers above the onset density given respectively by (B5) (2-D) and (3.8) (3-D). This instability sets in at the largest scale available in the system, typically the dimension of the experimental set-up or of the simulation box. Furthermore, due to the incompressible nature of the embedding fluid, dilute 2-D and 3-D bulk suspensions of microswimmers are always stable towards fluctuations in the microswimmer density.
In contrast, we showed that a 2-D layer of microswimmers embedded in a 3-D fluid is unstable for both pushers and pullers. For the former swimmer class, an orientational instability similar to the pusher instability in a bulk fluid occurs for large enough densities. However, in contrast to the bulk case, the orientational instability in the 2-D layer sets in at the smallest spatial scale, which we interpret as the one below which our continuum description is not valid anymore, i.e. the average particle–particle separation. For parameter values roughly corresponding to E. coli bacteria, this leads to the instability setting in at a length scale of ![]() $\sim 5\ \mathrm {\mu }$m, comparable to the bacterial dimensions.
$\sim 5\ \mathrm {\mu }$m, comparable to the bacterial dimensions.
On the other hand, a layer of puller microswimmers is susceptible to a density instability characterised by spatial aggregation of microswimmers independent of their orientations. This instability is caused by the mutual advection of the microswimmers and is the direct consequence of the sink-like nature of their in-plane velocity fields, as discussed in § 1. In the thermodynamic limit, the puller suspension is unstable at any density, while a non-zero critical density emerges for finite system sizes, as shown in (4.16). The scale at which this puller instability sets in depends on the microswimmer density: at small and moderate densities, the instability occurs at long length scales, while at high enough densities it is replaced by a small-scale instability. While the cross-over between these two regimes depends on the particle shape through ![]() $B$, both instabilities are generically present regardless of particle shape. Whether this implies that the system reaches different steady states at long times is still an open question that we leave for future work. We also note that the density instability presented here is qualitatively similar to the instability reported by Baskaran & Marchetti (Reference Baskaran and Marchetti2009), as both are caused by the fluid's compressibility; in the case of Baskaran & Marchetti (Reference Baskaran and Marchetti2009), however, the compressibility arises as a result of an erroneous coarse-graining procedure, as discussed by Aranson (Reference Aranson2022).
$B$, both instabilities are generically present regardless of particle shape. Whether this implies that the system reaches different steady states at long times is still an open question that we leave for future work. We also note that the density instability presented here is qualitatively similar to the instability reported by Baskaran & Marchetti (Reference Baskaran and Marchetti2009), as both are caused by the fluid's compressibility; in the case of Baskaran & Marchetti (Reference Baskaran and Marchetti2009), however, the compressibility arises as a result of an erroneous coarse-graining procedure, as discussed by Aranson (Reference Aranson2022).
We would like to stress once more that the instability scenarios discussed here are not the consequence of the spatial dimensionality, as 2-D and 3-D bulk suspensions exhibit qualitatively a very similar behaviour. Instead, the qualitative differences to the corresponding bulk suspensions come from the fact that the in-plane fluid in which the microswimmers move is effectively compressible, an effect which is generically present in the case of motion restricted to a subset of the embedding space, including microswimmer layers in the vicinity of solid and liquid boundaries. Importantly, this effect is likely to be one of the main driving forces behind the boundary-induced clustering and phase separation observed in self-propelled suspension droplets (Thutupalli et al. Reference Thutupalli, Geyer, Singh, Adhikari and Stone2018) and squirmer suspensions (Singh & Adhikari Reference Singh and Adhikari2016). These authors highlight the importance of the presence of a boundary in inducing effective in-plane attractions among puller swimmers after accumulating at the surface or interface, although they rationalise their findings in terms of attractive hydrodynamic forces without explicitly mentioning the effective compressibility mechanism present in this geometry. Thus, even though our chosen geometry of a 2-D plane in an infinite 3-D fluid seems artificial, we argue that the generic mechanism demonstrated here is in fact an important driving force behind accumulation in active-particle suspensions near interfaces.
Furthermore, the phenomenon of effective in-plane compressibility is not limited to dipolar flow fields. As demonstrated by Spagnolie & Lauga (Reference Spagnolie and Lauga2012), all flow singularities relevant to self-propulsion of microorganisms can be obtained by repeatedly applying the ![]() $(\boldsymbol {p} \boldsymbol {\cdot } \boldsymbol {\nabla })$ operator to the stokeslet and the point source singularity. Therefore, these singularities will have alternating parities with respect to the angle defined by
$(\boldsymbol {p} \boldsymbol {\cdot } \boldsymbol {\nabla })$ operator to the stokeslet and the point source singularity. Therefore, these singularities will have alternating parities with respect to the angle defined by ![]() $\boldsymbol {x} \boldsymbol {\cdot } \boldsymbol {p}$. In the context of the calculation presented in § 1, this leads to a layer of force dipoles, force octupoles and so on having effectively compressible in-plane velocity fields, while the remaining flow singularities remain incompressible even when restricted to a lower-dimensional subset of the embedding space. The same reasoning holds for the source singularities, where sources, source quadrupoles and so on exhibit effectively compressible in-plane velocity fields. Our findings are therefore likely to be of more general importance for hydrodynamic interactions and collective motion of realistic microorganisms near boundaries.
$\boldsymbol {x} \boldsymbol {\cdot } \boldsymbol {p}$. In the context of the calculation presented in § 1, this leads to a layer of force dipoles, force octupoles and so on having effectively compressible in-plane velocity fields, while the remaining flow singularities remain incompressible even when restricted to a lower-dimensional subset of the embedding space. The same reasoning holds for the source singularities, where sources, source quadrupoles and so on exhibit effectively compressible in-plane velocity fields. Our findings are therefore likely to be of more general importance for hydrodynamic interactions and collective motion of realistic microorganisms near boundaries.
One of the remaining open questions pertains to the stability of a sheet of microswimmers with respect to out-of-plane perturbations. At first glance, a sheet of pushers generates on average a fluid flow towards the sheet along the third direction and one thus expects out-of-plane perturbations to be suppressed by such a flow. By the same argument, the opposite is expected for pullers. Some support for this hypothesis can be drawn from Ishikawa & Pedley (Reference Ishikawa and Pedley2008), who simulated a collection of spherical squirmers confined to a single layer, as in our set-up. They observed no instability for pushers, while pullers exhibited formation of dense clusters visually consistent with our density instability. Interestingly, when bottom-heavy puller squirmers were allowed to move out of the original monolayer, the authors observed the formation of a dynamical steady state in a form of a microswimmer band, suggesting that pullers are indeed unstable with respect to out-of-plane perturbations. In contrast, the continuum simulations by Nejad & Yeomans (Reference Nejad and Yeomans2022) showed coexisting regions of in-plane and out-of-plane director orientations in extensile active nematics, while no such instability was present in the corresponding contractile systems. This complex picture clearly has to be understood via a combination of linear stability analysis and fully nonlinear simulations, a question that we leave open to future studies. We stress, however, that we view the set-up considered in this work as a way to isolate the effect of in-plane compressibility on collective motion of experimental realisations of microswimmers accumulated close to a physical boundary. In such systems, there are always additional effects ensuring microswimmers’ presence at the boundary, e.g. gravity or surface tension, and the question of stability with respect to out-of-plane perturbations should be addressed in that context.
We conclude by observing that, while the linear stability analysis presented here identifies the origin, the onset conditions and the associated scales of the instabilities, their nonlinear evolution and ensuing non-equilibrium steady states must be assessed in numerical simulations of particle-based models (Bárdfalvy et al. Reference Bárdfalvy, Nordanger, Nardini, Morozov and Stenhammar2019, Reference Bárdfalvy, Anjum, Nardini, Morozov and Stenhammar2020) or mean-field moment equations (Saintillan & Shelley Reference Saintillan and Shelley2013). We aim to further explore this and similar questions in future studies.
Funding
J.S. acknowledges financial support from the Swedish Research Council (project no. 2019-03718). A.M. acknowledges financial support from EPSRC (grant no. EP/V048198/1). C.N. acknowledges funding from Institut de physique du CNRS.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Dipolar fluid velocity
The far-field fluid velocity ![]() $\boldsymbol {u}$ generated by a swimming microorganism at low Reynolds number is described by the hydrodynamic force dipole (Lauga & Powers Reference Lauga and Powers2009; Spagnolie & Lauga Reference Spagnolie and Lauga2012). The latter satisfies Stokes’ equation driven by two point-like forces
$\boldsymbol {u}$ generated by a swimming microorganism at low Reynolds number is described by the hydrodynamic force dipole (Lauga & Powers Reference Lauga and Powers2009; Spagnolie & Lauga Reference Spagnolie and Lauga2012). The latter satisfies Stokes’ equation driven by two point-like forces ![]() $\pm f \boldsymbol {p}$ acting on the fluid at the positions
$\pm f \boldsymbol {p}$ acting on the fluid at the positions ![]() $\pm \tfrac {1}{2}l\boldsymbol {p}$
$\pm \tfrac {1}{2}l\boldsymbol {p}$
Here, ![]() $\mu$ is the viscosity of the fluid,
$\mu$ is the viscosity of the fluid, ![]() $P$ is the pressure and
$P$ is the pressure and ![]() $\delta (\boldsymbol {x})$ denotes the Dirac delta function. The solution to this system is readily found by performing the
$\delta (\boldsymbol {x})$ denotes the Dirac delta function. The solution to this system is readily found by performing the ![]() $d$-dimensional Fourier transform, (2.8a,b), which gives
$d$-dimensional Fourier transform, (2.8a,b), which gives
The point-dipole approximation, relevant at large scales where ![]() $k l \ll 1$, is obtained to linear order in the dipolar length
$k l \ll 1$, is obtained to linear order in the dipolar length ![]() $l$, yielding
$l$, yielding
Here, ![]() $\mathbb {P}^{\alpha \beta } = \delta ^{\alpha \beta } - k^{\alpha }k^{\beta }/k^{2}$ is the transverse projection operator,
$\mathbb {P}^{\alpha \beta } = \delta ^{\alpha \beta } - k^{\alpha }k^{\beta }/k^{2}$ is the transverse projection operator, ![]() $k=\vert \boldsymbol {k} \vert$, and
$k=\vert \boldsymbol {k} \vert$, and ![]() $\kappa = f l / \mu$ is the dipolar strength.
$\kappa = f l / \mu$ is the dipolar strength.
The derivation presented above is independent of the spatial dimensionality ![]() $d$ and the Fourier transform of the dipolar field (A5) has the same form for bulk systems of all dimensions. Its real-space representation, however, strongly depends on
$d$ and the Fourier transform of the dipolar field (A5) has the same form for bulk systems of all dimensions. Its real-space representation, however, strongly depends on ![]() $d$. In three dimensions, the inverse Fourier transform (2.8a,b) yields
$d$. In three dimensions, the inverse Fourier transform (2.8a,b) yields
where we have introduced an arbitrary position ![]() $\boldsymbol {x}_{0}$ of the force dipole. In two dimensions, the real-space representation is
$\boldsymbol {x}_{0}$ of the force dipole. In two dimensions, the real-space representation is
where we notice that the dipolar strength ![]() $\kappa = f l / \mu$ has different physical dimensions in 2-D and 3-D bulk systems.
$\kappa = f l / \mu$ has different physical dimensions in 2-D and 3-D bulk systems.
The velocity field of a hydrodynamic dipole restricted to a 2-D plane embedded in an infinite 3-D fluid can be obtained from (A6). We select ![]() $z=0$ to be the plane of the microswimmers, and recall the definitions of 2-D vectors
$z=0$ to be the plane of the microswimmers, and recall the definitions of 2-D vectors ![]() $\boldsymbol {\mathcal {x}}=(x,y)$, and
$\boldsymbol {\mathcal {x}}=(x,y)$, and ![]() $\boldsymbol {\mathcal {p}}=(p_x,p_y)$, from the main text. Performing the corresponding 2-D Fourier transform of (A6) with respect to
$\boldsymbol {\mathcal {p}}=(p_x,p_y)$, from the main text. Performing the corresponding 2-D Fourier transform of (A6) with respect to ![]() $\boldsymbol {\mathcal {x}}$, leads to
$\boldsymbol {\mathcal {x}}$, leads to
where ![]() $\boldsymbol {\mathcal {k}} = ( \mathcal {k}_x, \mathcal {k}_y )$ is the wave vector associated with
$\boldsymbol {\mathcal {k}} = ( \mathcal {k}_x, \mathcal {k}_y )$ is the wave vector associated with ![]() $\boldsymbol {\mathcal {x}}$, and we have introduced the longitudinal projection operator
$\boldsymbol {\mathcal {x}}$, and we have introduced the longitudinal projection operator ![]() $\mathbb {Q}^{\alpha \beta } = \mathcal {k}^{\alpha }\mathcal {k}^{\beta }/\mathcal {k}^{2}$.
$\mathbb {Q}^{\alpha \beta } = \mathcal {k}^{\alpha }\mathcal {k}^{\beta }/\mathcal {k}^{2}$.
Appendix B. Linear stability analysis of 2-D bulk suspensions
Here, we repeat the calculation presented in § 3 for the case of microswimmers suspended in 2-D bulk fluid. We set ![]() $d = 2$ in (2.13)–(2.14), and employ (A5), since the form of the dipolar Fourier transform is the same in all dimensions, as noted in Appendix A. We obtain the following eigenvalue problems:
$d = 2$ in (2.13)–(2.14), and employ (A5), since the form of the dipolar Fourier transform is the same in all dimensions, as noted in Appendix A. We obtain the following eigenvalue problems:
which, similarly to the 3-D case, are decoupled. The orientational eigenvalue problem can be rewritten as
where, as before, ![]() $b = v_{s}k/(\chi + \lambda )$. In contrast to (3.6), the solution to (B3) can be found analytically, yielding
$b = v_{s}k/(\chi + \lambda )$. In contrast to (3.6), the solution to (B3) can be found analytically, yielding
where ![]() $G(\gamma _{2d})$ is given in (4.8). The plot of
$G(\gamma _{2d})$ is given in (4.8). The plot of ![]() $G$ is shown in figure 5, and it has the same qualitative features as
$G$ is shown in figure 5, and it has the same qualitative features as ![]() $F(\gamma )$ shown in figure 2. As in the 3-D case, the orientational instability only exists for pushers,
$F(\gamma )$ shown in figure 2. As in the 3-D case, the orientational instability only exists for pushers, ![]() $\kappa >0$, and sets in at the largest possible scale,
$\kappa >0$, and sets in at the largest possible scale, ![]() $k \rightarrow 0$. The corresponding instability condition is given by
$k \rightarrow 0$. The corresponding instability condition is given by
where the number density ![]() $n$ and the dipolar strength
$n$ and the dipolar strength ![]() $\kappa$ have different dimensions than their 3-D counterparts. The solution (B4) ceases to exist for
$\kappa$ have different dimensions than their 3-D counterparts. The solution (B4) ceases to exist for ![]() $\gamma _{2d}>1/\sqrt {2}$, where one can instead prove stability using an analysis completely analogous to the 3-D case (see Appendix C.1). The analysis of density fluctuations is significantly simpler and the corresponding eigenvalue is readily obtained from (B1)
$\gamma _{2d}>1/\sqrt {2}$, where one can instead prove stability using an analysis completely analogous to the 3-D case (see Appendix C.1). The analysis of density fluctuations is significantly simpler and the corresponding eigenvalue is readily obtained from (B1)
Clearly, ![]() $\chi$ is negative for all
$\chi$ is negative for all ![]() $k$, and thus the suspension is always stable with respect to small fluctuations in microswimmer density.
$k$, and thus the suspension is always stable with respect to small fluctuations in microswimmer density.

Figure 5. The real (a) and imaginary (b) parts of the function ![]() $G(\gamma )$ from (4.8).
$G(\gamma )$ from (4.8).
Appendix C. Linear stability analysis using Laplace transforms
C.1. Density fluctuations in bulk suspensions
As mentioned in § 4.1, the linear stability analysis based on the ansatz (2.12) leads to a missing solution of the eigenvalue problem at small spatial scales. This issue can be tackled by exactly solving the linear dynamics (2.9) via Laplace transforms. We introduce the following notation for the forward Laplace transform:
where ![]() $s$ has a positive real part. For the inverse Laplace transformation, we use the definition
$s$ has a positive real part. For the inverse Laplace transformation, we use the definition
 \begin{equation} f(t) = \frac{1}{2{\rm \pi} {\rm i}} \lim_{T\rightarrow\infty} \int_{\gamma-i T}^{\gamma+i T} \,\mathrm{d} s \ f(s) \mathrm{e}^{st}, \end{equation}
\begin{equation} f(t) = \frac{1}{2{\rm \pi} {\rm i}} \lim_{T\rightarrow\infty} \int_{\gamma-i T}^{\gamma+i T} \,\mathrm{d} s \ f(s) \mathrm{e}^{st}, \end{equation}
where ![]() $\gamma$ must be chosen such that the real part of every pole in
$\gamma$ must be chosen such that the real part of every pole in ![]() $f(s)$ is smaller than
$f(s)$ is smaller than ![]() $\gamma$.
$\gamma$.
We now consider the case of a 3-D bulk suspension, for which the Laplace transform of (2.9) gives
where ![]() $\delta \hat {\varPsi }_{0} = \delta \hat {\varPsi }(\boldsymbol {k},\boldsymbol {p},t=0)$ represents the initial condition. Dividing the last equation with the linear operator on the left-hand side and integrating over the orientation
$\delta \hat {\varPsi }_{0} = \delta \hat {\varPsi }(\boldsymbol {k},\boldsymbol {p},t=0)$ represents the initial condition. Dividing the last equation with the linear operator on the left-hand side and integrating over the orientation ![]() $\boldsymbol {p}$ leads to
$\boldsymbol {p}$ leads to
 \begin{equation} \delta \hat{\rho}(s) = \frac{1}{1 - \dfrac{\lambda}{v_{s}k}\arctan\left(\dfrac{v_{s}k}{s + \lambda}\right)} \int \,\mathrm{d} \boldsymbol{p} \frac{\delta \hat{\varPsi}_{0}}{s + \lambda + {\rm i} v_{s} \boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k}}. \end{equation}
\begin{equation} \delta \hat{\rho}(s) = \frac{1}{1 - \dfrac{\lambda}{v_{s}k}\arctan\left(\dfrac{v_{s}k}{s + \lambda}\right)} \int \,\mathrm{d} \boldsymbol{p} \frac{\delta \hat{\varPsi}_{0}}{s + \lambda + {\rm i} v_{s} \boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k}}. \end{equation}The expression (C4) contains two separate poles
 \begin{equation} s_{1} ={-} \lambda - {\rm i} v_{s} \boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k}, \quad s_{2} ={-} \lambda + \frac{v_{s}k}{\tan\left(\dfrac{v_{s}k}{\lambda}\right)}, \end{equation}
\begin{equation} s_{1} ={-} \lambda - {\rm i} v_{s} \boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k}, \quad s_{2} ={-} \lambda + \frac{v_{s}k}{\tan\left(\dfrac{v_{s}k}{\lambda}\right)}, \end{equation}
where the second pole appears only in the limited region of parameter space ![]() $v_{s}k/\lambda < {\rm \pi}/2$. The result of the inverse Laplace transformation (C2) of (C4) consists of two terms, one corresponding to each pole
$v_{s}k/\lambda < {\rm \pi}/2$. The result of the inverse Laplace transformation (C2) of (C4) consists of two terms, one corresponding to each pole
which we now analyse separately. The first term in (C6) exists for any ![]() $v_{s}k/\lambda$ and reads
$v_{s}k/\lambda$ and reads
 \begin{equation} \delta \hat{\rho}_{1}(t) = \int \,\mathrm{d} \boldsymbol{p} \left[ \frac{1}{1 - \dfrac{\lambda}{v_{s}k}\arctan\left(\dfrac{{\rm i} k}{\boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k}}\right)} \exp({- \left( \lambda + iv_{s}\boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k} \right)t}) \right] \delta \hat{\varPsi}_{0}(\boldsymbol{k},\boldsymbol{p}). \end{equation}
\begin{equation} \delta \hat{\rho}_{1}(t) = \int \,\mathrm{d} \boldsymbol{p} \left[ \frac{1}{1 - \dfrac{\lambda}{v_{s}k}\arctan\left(\dfrac{{\rm i} k}{\boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k}}\right)} \exp({- \left( \lambda + iv_{s}\boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k} \right)t}) \right] \delta \hat{\varPsi}_{0}(\boldsymbol{k},\boldsymbol{p}). \end{equation}
The integral over ![]() $\boldsymbol {p}$ is conveniently expressed in spherical coordinates with its polar axis being along
$\boldsymbol {p}$ is conveniently expressed in spherical coordinates with its polar axis being along ![]() $\boldsymbol {k}$, and reads
$\boldsymbol {k}$, and reads
 \begin{align} \delta \hat{\rho}_{1}(t) = \mathrm{e}^{-\lambda t} \int_{{-}1}^{1} \,\mathrm{d} x \ F(x) \mathrm{exp}(- {\rm i}v_{s}k t x ), \quad F(x) = \frac{\int_{0}^{2{\rm \pi}} \,\mathrm{d} \phi\ \delta \hat{\varPsi}_{0}(\boldsymbol{k},\phi,\arccos(x))}{1 - \dfrac{\lambda}{v_{s}k}\arctan\left(\dfrac{{\rm i}}{x}\right)}. \end{align}
\begin{align} \delta \hat{\rho}_{1}(t) = \mathrm{e}^{-\lambda t} \int_{{-}1}^{1} \,\mathrm{d} x \ F(x) \mathrm{exp}(- {\rm i}v_{s}k t x ), \quad F(x) = \frac{\int_{0}^{2{\rm \pi}} \,\mathrm{d} \phi\ \delta \hat{\varPsi}_{0}(\boldsymbol{k},\phi,\arccos(x))}{1 - \dfrac{\lambda}{v_{s}k}\arctan\left(\dfrac{{\rm i}}{x}\right)}. \end{align}
We observe that ![]() $\int _{-1}^{1} \,\mathrm {d} x | F(x) |<\infty$, provided
$\int _{-1}^{1} \,\mathrm {d} x | F(x) |<\infty$, provided ![]() $\max _x |\int _{0}^{2{\rm \pi} } \,\mathrm {d} \phi \, \delta \hat {\varPsi }_{0}(\boldsymbol {k},\phi,\arccos (x))| < \infty$, as expected from a physical initial condition
$\max _x |\int _{0}^{2{\rm \pi} } \,\mathrm {d} \phi \, \delta \hat {\varPsi }_{0}(\boldsymbol {k},\phi,\arccos (x))| < \infty$, as expected from a physical initial condition ![]() $\delta \hat {\varPsi }(\boldsymbol {k},\boldsymbol {p})$. Applying the Riemann–Lebesgue lemma (Bender & Orszag Reference Bender and Orszag1999), we conclude that
$\delta \hat {\varPsi }(\boldsymbol {k},\boldsymbol {p})$. Applying the Riemann–Lebesgue lemma (Bender & Orszag Reference Bender and Orszag1999), we conclude that ![]() $\delta \hat {\rho }_{1}(t) \to 0$, as
$\delta \hat {\rho }_{1}(t) \to 0$, as ![]() $t\to \infty$ for
$t\to \infty$ for ![]() $v_s k>0$.
$v_s k>0$.
The second term in (C6) exists only for ![]() $v_{s}k/\lambda < {\rm \pi}/2$ and has the form
$v_{s}k/\lambda < {\rm \pi}/2$ and has the form
 \begin{align} \delta
\hat{\rho}_{2}(t) &= \exp\left[- \left(
\lambda-\frac{v_{s}k}{\tan(v_{s}k/\lambda)} \right)t
\right] \nonumber\\ &\quad \int \,\mathrm{d} \boldsymbol{p} \left[
\frac{\left(\dfrac{v_{s}k}{\lambda}\right)}{\tan\left(\dfrac{v_{s}k}{\lambda}\right)}
\frac{1 + \tan^{2}\left(\dfrac{v_{s}k}{\lambda}\right)}{1 +
{\rm
i}\tan\left(\dfrac{v_{s}k}{\lambda}\right)\boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k}
} \right] \delta
\hat{\varPsi}_{0}(\boldsymbol{k},\boldsymbol{p}).
\end{align}
\begin{align} \delta
\hat{\rho}_{2}(t) &= \exp\left[- \left(
\lambda-\frac{v_{s}k}{\tan(v_{s}k/\lambda)} \right)t
\right] \nonumber\\ &\quad \int \,\mathrm{d} \boldsymbol{p} \left[
\frac{\left(\dfrac{v_{s}k}{\lambda}\right)}{\tan\left(\dfrac{v_{s}k}{\lambda}\right)}
\frac{1 + \tan^{2}\left(\dfrac{v_{s}k}{\lambda}\right)}{1 +
{\rm
i}\tan\left(\dfrac{v_{s}k}{\lambda}\right)\boldsymbol{p}\boldsymbol{\cdot}\boldsymbol{k}
} \right] \delta
\hat{\varPsi}_{0}(\boldsymbol{k},\boldsymbol{p}).
\end{align}The temporal evolution of (C9) follows an exponential decay provided that
which always holds for ![]() $v_{s}k/\lambda < {\rm \pi}/2$.
$v_{s}k/\lambda < {\rm \pi}/2$. ![]() $\delta \hat {\rho }_2$ thus corresponds to the solution obtained when using the exponential ansatz
$\delta \hat {\rho }_2$ thus corresponds to the solution obtained when using the exponential ansatz ![]() $\delta \hat {\rho }(t) \sim \exp \{ s t \}$, as was analysed in § 3.2.
$\delta \hat {\rho }(t) \sim \exp \{ s t \}$, as was analysed in § 3.2.
We conclude that, although the use of the exponential ansatz in (2.12) does not allow for retrieving the sub-exponential contributions to the linear dynamics, the missing part does not carry any new information relevant for the linear stability analysis.
C.2. Orientational instability in a sheet of microswimmers
We now repeat the calculation for the case of transverse velocity fluctuations in a 2-D suspension restricted to a plane in a 3-D fluid. The starting point is the Smoluchowski equation (2.9) in two dimensions
Equation (C11) is now transformed using (C1), and after multiplying with ![]() $\mathbb {P}^{\alpha \beta }\hat {u}^{\beta }_{plane}$ and integrating over the orientation
$\mathbb {P}^{\alpha \beta }\hat {u}^{\beta }_{plane}$ and integrating over the orientation ![]() $\boldsymbol {\mathcal {p}}$, we arrive at
$\boldsymbol {\mathcal {p}}$, we arrive at
 \begin{equation} \delta \hat{\mathcal{U}}_{{\perp}}^{\alpha}(s) = \frac{1}{1 - M_{11}} \int_{0}^{2{\rm \pi}} \frac{\mathrm{d} \theta}{2{\rm \pi}} \frac{ \mathbb{P}^{\alpha\beta} \hat{u}_{plane}^{\beta} \delta \hat{\varPsi}_0(\boldsymbol{\mathcal{k}},\theta)}{s + \lambda + {\rm i} v_s \mathcal{k} \cos\theta}, \end{equation}
\begin{equation} \delta \hat{\mathcal{U}}_{{\perp}}^{\alpha}(s) = \frac{1}{1 - M_{11}} \int_{0}^{2{\rm \pi}} \frac{\mathrm{d} \theta}{2{\rm \pi}} \frac{ \mathbb{P}^{\alpha\beta} \hat{u}_{plane}^{\beta} \delta \hat{\varPsi}_0(\boldsymbol{\mathcal{k}},\theta)}{s + \lambda + {\rm i} v_s \mathcal{k} \cos\theta}, \end{equation}
where ![]() $M_{11}$ is defined in (4.4). Similarly to before, the inverse Laplace transform consists of two parts, each corresponding to one of the poles in (C12). The first one is the pole corresponding to
$M_{11}$ is defined in (4.4). Similarly to before, the inverse Laplace transform consists of two parts, each corresponding to one of the poles in (C12). The first one is the pole corresponding to ![]() $M_{11}=1$, which leads to the dispersion law in (4.7). As discussed in the main text, the latter solution ceases to exist for
$M_{11}=1$, which leads to the dispersion law in (4.7). As discussed in the main text, the latter solution ceases to exist for ![]() $2\sqrt {2} v_{s} > B \kappa n$. In this region, the stability is instead determined by the second pole
$2\sqrt {2} v_{s} > B \kappa n$. In this region, the stability is instead determined by the second pole ![]() $s = -\lambda - \textrm {i} v_{s} \mathcal {k} \cos \theta$, where the time representation of the corresponding solution is given by
$s = -\lambda - \textrm {i} v_{s} \mathcal {k} \cos \theta$, where the time representation of the corresponding solution is given by
 \begin{equation} \delta \hat{\mathcal{U}}_{{\perp}}^{\alpha}(t) = \mathrm{e}^{-\lambda t} \int_{0}^{2{\rm \pi}} \,\mathrm{d} \theta \, F(\theta) \mathrm{exp}(- {\rm i}v_{s} \mathcal{k} t \cos\theta), \quad F(\theta) = \frac{\mathbb{P}^{\alpha\beta} \hat{u}_{plane}^{\beta} \delta \hat{\varPsi}_0(\boldsymbol{\mathcal{k}},\theta)}{1 - M_{11}|_{b\rightarrow{{\rm i}}/{\cos\theta}}}. \end{equation}
\begin{equation} \delta \hat{\mathcal{U}}_{{\perp}}^{\alpha}(t) = \mathrm{e}^{-\lambda t} \int_{0}^{2{\rm \pi}} \,\mathrm{d} \theta \, F(\theta) \mathrm{exp}(- {\rm i}v_{s} \mathcal{k} t \cos\theta), \quad F(\theta) = \frac{\mathbb{P}^{\alpha\beta} \hat{u}_{plane}^{\beta} \delta \hat{\varPsi}_0(\boldsymbol{\mathcal{k}},\theta)}{1 - M_{11}|_{b\rightarrow{{\rm i}}/{\cos\theta}}}. \end{equation}
Again, it is possible to show that ![]() $\int _{0}^{2{\rm \pi} } \,\mathrm {d} \theta | F(\theta ) |$ is bounded provided
$\int _{0}^{2{\rm \pi} } \,\mathrm {d} \theta | F(\theta ) |$ is bounded provided ![]() $2\sqrt {2} v_s > B\kappa n$ and
$2\sqrt {2} v_s > B\kappa n$ and ![]() $\delta \hat {\varPsi }_0(\boldsymbol {\mathcal {k}},\theta )$ satisfies the same physical requirements as in Appendix C.1. Applying the Riemann–Lebesgue lemma, we conclude that
$\delta \hat {\varPsi }_0(\boldsymbol {\mathcal {k}},\theta )$ satisfies the same physical requirements as in Appendix C.1. Applying the Riemann–Lebesgue lemma, we conclude that ![]() $\delta \hat {\mathcal {U}}_{\perp }^{\alpha }(t)$ vanishes as
$\delta \hat {\mathcal {U}}_{\perp }^{\alpha }(t)$ vanishes as ![]() $t \to \infty$, and the system is stable for
$t \to \infty$, and the system is stable for ![]() $2\sqrt {2} v_s > B\kappa n$.
$2\sqrt {2} v_s > B\kappa n$.
Appendix D. Approximation of  $n_c$ for a sheet of pushers
$n_c$ for a sheet of pushers
In this appendix, we will derive the approximate expression (4.12) for the critical density ![]() $n_c$ corresponding to the orientational instability setting in at the scale of particle–particle separation in a 2-D layer of pusher microswimmers. We set
$n_c$ corresponding to the orientational instability setting in at the scale of particle–particle separation in a 2-D layer of pusher microswimmers. We set ![]() $\mathcal {k}_{c} = \sqrt {{\rm \pi} ^{3}n_{c}}$ and
$\mathcal {k}_{c} = \sqrt {{\rm \pi} ^{3}n_{c}}$ and ![]() $n=n_c$ in (4.7), giving
$n=n_c$ in (4.7), giving
We now separate the expression into two approximations valid asymptotically for small and large values of ![]() $v_{s}$. We first set
$v_{s}$. We first set ![]() $v_{s} \rightarrow 0$ in (D1), yielding
$v_{s} \rightarrow 0$ in (D1), yielding
where ![]() $\textrm {Re}[\chi ] = 0$ now gives the ‘shaker’ approximation
$\textrm {Re}[\chi ] = 0$ now gives the ‘shaker’ approximation
 \begin{equation} n_{c}(v_s \to 0) = \frac{4}{\rm \pi} \left( \frac{\lambda}{B \kappa} \right)^{2/3}. \end{equation}
\begin{equation} n_{c}(v_s \to 0) = \frac{4}{\rm \pi} \left( \frac{\lambda}{B \kappa} \right)^{2/3}. \end{equation}For the fast-swimming limit, we use the result (4.10), i.e. we assume that the critical density is linearly proportional to the swimming speed
Combining (D3) and (D4) gives the result (4.12). The latter shows a good quantitative agreement with the numerical solution of ![]() $\textrm {Re}[\chi ] = 0$, as shown in figure 6.
$\textrm {Re}[\chi ] = 0$, as shown in figure 6.

Figure 6. Comparison of the approximation (4.12) with the exact values obtained by numerical solution of ![]() $\textrm {Re}[\chi ] = 0$, where
$\textrm {Re}[\chi ] = 0$, where ![]() $\chi$ is given by (D1). Our approximation shows good quantitative agreement with the exact numerical values. The kink in the numerical data is not an artefact and corresponds to a switch between two eigenvalue branches.
$\chi$ is given by (D1). Our approximation shows good quantitative agreement with the exact numerical values. The kink in the numerical data is not an artefact and corresponds to a switch between two eigenvalue branches.