Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T13:49:07.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydrodynamic force and torque acting on a micron-sized spherical particle attached to a surface with large-scale concave roughness in linear shear flow and the possibility of detachment

Published online by Cambridge University Press:  24 August 2022

Kun Meng ,
Yequ Pang ,
Yinshui Liu  and
Yan Cui Open the ORCID record for Yan Cui [Opens in a new window]
Kun Meng
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Luoyu Road 1037, 430074 Wuhan, PR China
Yequ Pang
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Luoyu Road 1037, 430074 Wuhan, PR China
Yinshui Liu
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Luoyu Road 1037, 430074 Wuhan, PR China
Yan Cui*
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Luoyu Road 1037, 430074 Wuhan, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

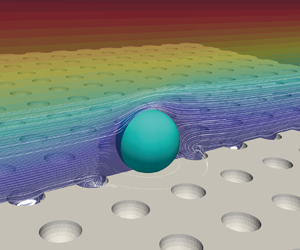
This work studies the detachment of a micron-sized spherical particle from a surface with concave roughness in a linear shear flow. The concave roughness is described as regularly spaced hollow hemispheres below a flat surface and is characterised by two dimensionless parameters, i.e. dimensionless asperity distance and asperity size ratio. The hydrodynamic force and torque on the particle are calculated by performing lattice Boltzmann simulations for particle Reynolds numbers ranging from 0.02 to 40. Empirical correlations of the drag, lift and torque coefficients of the particle as functions of the particle Reynolds number and the asperity size ratio are proposed. For detachment by lifting, sliding and rolling, a numerical approach to calculate the critical particle Reynolds number (i.e. above which the particle can detach from the surface) is proposed. It is found that the dimensionless asperity distance and the distribution of asperities on the rough surface have a minor influence on the hydrodynamic force and torque on the particle, and the detachment of the particle becomes more difficult as the particle sits deeper in a larger hole. Both the empirical correlations and the numerical approach can be implemented into Lagrangian particle tracking and can accurately predict the detachment of particles from the surface with concave roughness or the detachment of particles embedded in a flat surface.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 947 , 25 September 2022 , A27
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bhattacharjee, S., Ko, C.-H. & Elimelech, M. 1998 DLVO interaction between rough surfaces. Langmuir 14, 3365–3375.CrossRefGoogle Scholar
Bouzidi, M., Firdaouss, M. & Lallemand, P. 2001 Momentum transfer of a Boltzmann-lattice fluid with boundaries. Phys. Fluids 13, 3452–3459.CrossRefGoogle Scholar
Cui, Y., Schmalfuß, S., Zellnitz, S., Sommerfeld, M. & Urbanetz, N. 2014 Towards the optimisation and adaptation of dry powder inhalers. Intl J. Pharm. 470, 120–132.CrossRefGoogle ScholarPubMed
Cui, Y. & Sommerfeld, M. 2015 Forces on micron-sized particles randomly distributed on the surface of larger particles and possibility of detachment. Intl J. Multiphase Flow 72, 39–52.CrossRefGoogle Scholar
Cui, Y. & Sommerfeld, M. 2017 Application of lattice-Boltzmann method for analysing detachment of micron-sized particles from carrier particles in turbulent flows. Flow Turbul. Combust. 100, 271–297.CrossRefGoogle Scholar
Cui, Y. & Sommerfeld, M. 2022 Lattice–Boltzmann simulations for analysing the detachment of micron-sized spherical particles from surfaces with large-scale roughness structures. Particuology 61, 47–59.CrossRefGoogle Scholar
Derjaguin, B., Muller, V. & Toporov, Y. 1975 Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 53, 314–326.CrossRefGoogle Scholar
D'Humieres, D. 1994 Generalized lattice-Boltzmann equations. In Rarefied Gas Dynamics: Theory and Simulations, pp. 450–458. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Goldman, A., Cox, R. & Brenner, H. 1967 Slow viscous motion of a sphere parallel to a plane wall–II Couette flow. Chem. Engng Sci. 22, 653–660.CrossRefGoogle Scholar
Guo, Z., Zheng, C. & Shi, B. 2002 An extrapolation method for boundary conditions in lattice Boltzmann method. Phys. Fluids 14, 2007–2010.CrossRefGoogle Scholar
Henry, C. & Minier, J.-P. 2014 Progress in particle resuspension from rough surfaces by turbulent flows. Prog. Energy Combust. Sci. 45, 1–53.CrossRefGoogle Scholar
Henry, C., Minier, J.-P., Lefevre, G. & Hurisse, O. 2011 Numerical study on the deposition rate of hematite particle on polypropylene walls: role of surface roughness. Langmuir 27, 4603–4612.CrossRefGoogle Scholar
Johnson, K., Kendall, K. & Roberts, A.D. 1971 Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A. Math. Phys. Sci. 324, 301–313.Google Scholar
Lee, H. & Balachandar, S. 2010 Drag and lift forces on a spherical particle moving on a wall in a shear flow at finite $Re$. J. Fluid Mech. 657, 89–125.CrossRefGoogle Scholar
Leighton, D. & Acrivos, A. 1985 The lift on a small sphere touching a plane in the presence of a simple shear flow. Z. Angew. Math. Phys. 36, 174–178.CrossRefGoogle Scholar
Li, K. & Zhong, C. 2016 Aeroacoustic simulations using compressible lattice Boltzmann method. Adv. Appl. Math. Mech. 8, 795–809.CrossRefGoogle Scholar
Nasr, B., Ahmadi, G., Ferro, A.R. & Dhaniyala, S. 2019 A model for particle removal from surfaces with large-scale roughness in turbulent flows. Aerosol Sci. Technol. 54, 291–303.CrossRefGoogle Scholar
O'Neill, M. 1968 A sphere in contact with a plane wall in a slow linear shear flow. Chem. Engng Sci. 23, 1293–1298.CrossRefGoogle Scholar
Reeks, M. & Hall, D. 2001 Kinetic models for particle resuspension in turbulent flows: theory and measurement. J. Aerosol Sci. 32, 1–31.CrossRefGoogle Scholar
Renner, N., Steckel, H., Urbanetz, N. & Scherließ, R. 2017 Nano- and microstructured model carrier surfaces to alter dry powder inhaler performance. Intl J. Pharm. 518, 20–28.CrossRefGoogle ScholarPubMed
Schiller, L. & Naumann, A. 1933 Uber die grundegenden berch-nungen bei der schwerkraftaufbereitung. Z. Verein. Deutsch. Ing. 77, 318–320.Google Scholar
Sommerfeld, M. & Schmalfuß, S. 2015 Numerical analysis of carrier particle motion in a dry powder inhaler. Trans. ASME J. Fluids Engng 138, 041308.CrossRefGoogle Scholar
Sommerfeld, M., van Wachem, B. & Oliemans, R. 2008 ERCOFTAC Best Practice Guidelines: Computational Fluid Dynamics of Dispersed Multi-Phase Flows. ERCOFTAC.Google Scholar
Xiao, J., Luo, Y., Niu, M., Wang, Q., Wu, J., Liu, X. & Xu, J. 2019 Study of imbibition in various geometries using phase field method. Capillarity 2, 57–65.CrossRefGoogle Scholar
Zellnitz, S., Zellnitz, L., Müller, M., Meindl, C., Schröttner, H. & Fröhlich, E. 2019 Impact of drug particle shape on permeability and cellular uptake in the lung. Eur. J. Pharm. Sci. 139, 105065.CrossRefGoogle ScholarPubMed
Zeng, L., Najjar, F., Balachandar, S. & Fischer, P. 2009 Forces on a finite-sized particle located close to a wall in a linear shear flow. Phys. Fluids 21, 033302.CrossRefGoogle Scholar
Ziskind, G., Fichman, M. & Gutfinger, C. 1997 Adhesion moment model for estimating particle detachment from a surface. J. Aerosol Sci. 28, 623–634.CrossRefGoogle Scholar
Supplementary material: File

Meng et al. supplementary material

Meng et al. supplementary material

Download Meng et al. supplementary material(File)
File 1.2 KB