The hydrodynamic diffusion of sedimenting point particles in a vertically sheared periodic system is investigated numerically and theoretically. In both the velocity-gradient direction and the vorticity direction, the rate of hydrodynamic diffusion is reduced as the shear rate is increased. In the velocity-gradient direction, two-particle interactions cause no net displacement, and three-particle interactions are necessary for diffusive behaviour. In contrast to an unsheared system, the resulting diffusion coefficient is only weakly dependent upon the size of the system and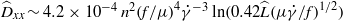 
${\widehat{D}}_{xx} \sim 4. 2\times 1{0}^{- 4} \hspace{0.167em} {n}^{2} {(f/ \mu )}^{4} {\dot {\gamma } }^{- 3} \ln (0. 42\widehat{L}{(\mu \dot {\gamma } / f)}^{1/ 2} )$, where 
$n$ is the particle number density,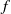 
$f$ the force per particle, 
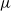$\mu $ the fluid viscosity, 
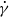$\dot {\gamma } $ the imposed shear rate, and 
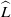$\widehat{L}$ the system size. In the vorticity direction, although individual two-particle interactions cause no net displacement, a superposition of interactions is sufficient to cause diffusion-like linear growth of the ensemble-averaged square particle displacements. The associated diffusion coefficient is given by 
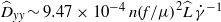${\widehat{D}}_{yy} \sim 9. 47\times 1{0}^{- 4} \hspace{0.167em} n{(f/ \mu )}^{2} \widehat{L}\hspace{0.167em} {\dot {\gamma } }^{- 1} $. At sufficiently long times, the effect of multi-particle interactions cannot be neglected and there is a transition to another regime in which the diffusion coefficient is similar in form, but slightly reduced from this value. The dependence of 
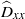${\widehat{D}}_{xx} $ and 
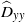${\widehat{D}}_{yy} $ on the number density and dimensionless shear rate is explained using theoretical scaling arguments and analyses.
