1. Introduction
Inertial particles settling in turbulent flows are important in many environmental and biological problems, ranging from cloud microphysics (Pruppacher & Klett Reference Pruppacher and Klett1997; Grabowski & Wang Reference Grabowski and Wang2013), dispersion of pollutants in the atmosphere (Dhariwal & Bragg Reference Dhariwal and Bragg2019; Toscano et al. Reference Toscano, Marro, Mele, Murena and Salizzoni2021) to aerosol deposition in human lungs (Chen et al. Reference Chen, Zhong, Tom, Kleinstreuer, Feng and He2016; Ou et al. Reference Ou, Jian and Deng2020). Understanding the physical mechanisms responsible for the modification of the particle settling velocity due to turbulence and its dependence on the system parameters is an important and ongoing research topic. Even for the simplest case of small, heavy, spherical inertial particles settling in homogeneous turbulent flows, the problem is very challenging to understand, and there remain many unanswered questions.
One key feature that has frequently been observed is that inertial particles settling in turbulence fall faster on average than they would in a quiescent fluid (Maxey Reference Maxey1987; Wang & Maxey Reference Wang and Maxey1993; Aliseda et al. Reference Aliseda, Cartellier, Hainaux and Lasheras2002; Good et al. Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014; Ireland, Bragg & Collins Reference Ireland, Bragg and Collins2016b; Momenifar, Dhariwal & Bragg Reference Momenifar, Dhariwal and Bragg2019; Petersen, Baker & Coletti Reference Petersen, Baker and Coletti2019; Momenifar & Bragg Reference Momenifar and Bragg2020). It has also been suggested that turbulence could lead to a reduction in the particle settling velocity, an effect referred to as ‘loitering’ (Nielsen Reference Nielsen1993). Although there is some evidence of loitering occurring in certain parameter regimes, e.g. see Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014), this remains controversial, and the majority of the evidence points to a settling enhancement, rather than reduction. Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) suggested, by comparing direct numerical simulations (DNS) of small, heavy inertial particles using linear and nonlinear drag, that loitering can only occur if the particles experience significant nonlinear drag forces. However, a subsequent DNS study by Rosa et al. (Reference Rosa, Parishani, Ayala and Wang2016) called that conclusion into question, finding that linear and nonlinear drag models gave virtually identical results showing only enhanced settling due to turbulence. Rosa et al. (Reference Rosa, Parishani, Ayala and Wang2016) suggested that a possible explanation for the discrepancy is that the DNS of Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) were not run for sufficiently long times for the particle settling velocities to statistically converge. This is a point we will return to later.
The particle inertia can be quantified by the Kolmogorov-scale Stokes number, ![]() $St$, that is defined as the ratio between the particle response time
$St$, that is defined as the ratio between the particle response time ![]() $\tau _p$ and the Kolmogorov time
$\tau _p$ and the Kolmogorov time ![]() $\tau _\eta$. The settling number
$\tau _\eta$. The settling number ![]() $\textit {Sv}\equiv \tau _p g /u_\eta$ quantifies the particle settling velocity in a quiescent fluid (i.e. the Stokes settling velocity
$\textit {Sv}\equiv \tau _p g /u_\eta$ quantifies the particle settling velocity in a quiescent fluid (i.e. the Stokes settling velocity ![]() $\tau _p g$, where g is the gravitational acceleration) relative to the Kolmogorov velocity
$\tau _p g$, where g is the gravitational acceleration) relative to the Kolmogorov velocity ![]() $u_\eta$. One may also use the Froude number
$u_\eta$. One may also use the Froude number ![]() $\textit {Fr}\equiv a_\eta /g$ that compares the Kolmogorov acceleration with that of gravity. The two numbers,
$\textit {Fr}\equiv a_\eta /g$ that compares the Kolmogorov acceleration with that of gravity. The two numbers, ![]() $\textit {St}$ and
$\textit {St}$ and ![]() $\textit {Sv}=\textit {St}/\textit {Fr}$, may be used to fully characterize an idealized one-way-coupled (1WC) system, in which the carrier fluid drives the motion of the particles, while the force from the particles on the fluid is assumed negligible. Such an idealized system is thought to be a good approximation when the particle mass loading is sufficiently small. A two-way-coupled (2WC) system is characterized by additional parameters such as the particle volume fraction
$\textit {Sv}=\textit {St}/\textit {Fr}$, may be used to fully characterize an idealized one-way-coupled (1WC) system, in which the carrier fluid drives the motion of the particles, while the force from the particles on the fluid is assumed negligible. Such an idealized system is thought to be a good approximation when the particle mass loading is sufficiently small. A two-way-coupled (2WC) system is characterized by additional parameters such as the particle volume fraction ![]() $\varPhi _v\equiv ({\rm \pi} /6) N_p (d_p/L)^3$ (for spherical particles in a cubic flow domain), where
$\varPhi _v\equiv ({\rm \pi} /6) N_p (d_p/L)^3$ (for spherical particles in a cubic flow domain), where ![]() $d_p$ is the particle diameter,
$d_p$ is the particle diameter, ![]() $N_p$ is the number of particles in the flow,
$N_p$ is the number of particles in the flow, ![]() $L$ is the length of the flow domain and the mass fraction,
$L$ is the length of the flow domain and the mass fraction, ![]() $\varPhi _m\equiv (\rho _p /\rho _f) \varPhi _v$, where
$\varPhi _m\equiv (\rho _p /\rho _f) \varPhi _v$, where ![]() $\rho _p /\rho _f$ is the ratio of the particle density to the fluid density. We are concerned with dilute suspensions, i.e.
$\rho _p /\rho _f$ is the ratio of the particle density to the fluid density. We are concerned with dilute suspensions, i.e. ![]() $\varPhi _v<10^{-3}$, of particles that are small, meaning
$\varPhi _v<10^{-3}$, of particles that are small, meaning ![]() $d_p/\eta \ll 1$ (where
$d_p/\eta \ll 1$ (where ![]() $\eta$ is the Kolmogorov length scale), and heavy, meaning
$\eta$ is the Kolmogorov length scale), and heavy, meaning ![]() $\rho _p/\rho _f\gg 1$, which is appropriate for diverse physical systems, from droplet dynamics in atmospheric clouds (Pruppacher & Klett Reference Pruppacher and Klett1997) to the transport of pharmaceutical nasal sprays (Kolanjiyil et al. Reference Kolanjiyil, Hosseini, Alfaifi, Hindle, Golshahi and Longest2021).
$\rho _p/\rho _f\gg 1$, which is appropriate for diverse physical systems, from droplet dynamics in atmospheric clouds (Pruppacher & Klett Reference Pruppacher and Klett1997) to the transport of pharmaceutical nasal sprays (Kolanjiyil et al. Reference Kolanjiyil, Hosseini, Alfaifi, Hindle, Golshahi and Longest2021).
In the context of 1WC systems, a key study that provided new insights into the physical mechanism by which turbulence modifies the settling velocities of inertial particles was that of Maxey (Reference Maxey1987), who showed that in the presence of gravity, particles tend to fall around the downward moving side of vortices in the flow. As a result of this, they fall faster on average in a turbulent flow than they would in a quiescent flow, an effect later referred to as the ‘preferential sweeping’ mechanism (Wang & Maxey Reference Wang and Maxey1993). The preferential sweeping mechanism arises due to two effects in the system. First, Maxey (Reference Maxey1987) argued that inertial particles are centrifuged out from vortices in the flow, causing them to preferentially sample strain-dominated regions. This was subsequently observed and confirmed using DNS by Squires & Eaton (Reference Squires and Eaton1990) and Yoshimoto & Goto (Reference Yoshimoto and Goto2007) later provided evidence for the multiscale nature of preferential concentration. Second, Maxey (Reference Maxey1987) argued that while the centrifuge effect causes the particles to move around the vortices in the flow, gravity causes them to be preferentially swept around the downward side of the vortices (because that is the ‘path of least resistance’ as pointed out in Tom & Bragg Reference Tom and Bragg2019), such that they preferentially follow regions of the flow where the fluid velocity points in the direction of gravity. This preferential sweeping effect was observed and confirmed using DNS in Wang & Maxey (Reference Wang and Maxey1993). Several subsequent numerical and experimental studies provided confirmation of settling enhancement due to the preferential sweeping effect (Bec, Homann & Ray Reference Bec, Homann and Ray2014; Ireland et al. Reference Ireland, Bragg and Collins2016b; Rosa et al. Reference Rosa, Parishani, Ayala and Wang2016; Petersen et al. Reference Petersen, Baker and Coletti2019; Li et al. Reference Li, Abraham, Guala and Hong2021b). In the original study of Maxey (Reference Maxey1987), the preferential sweeping mechanism was described theoretically for particles with weak inertia, i.e. ![]() $\textit {St}\ll 1$. The theory was recently extended to finite Stokes numbers by Tom & Bragg (Reference Tom and Bragg2019), revealing the role played in the preferential sweeping mechanism by vortices of different sizes and the
$\textit {St}\ll 1$. The theory was recently extended to finite Stokes numbers by Tom & Bragg (Reference Tom and Bragg2019), revealing the role played in the preferential sweeping mechanism by vortices of different sizes and the ![]() $St$ and
$St$ and ![]() $Fr$ dependence of the ‘multiscale preferential sweeping’ mechanism. It should also be noted that most of these studies focused on homogeneous turbulence (which is also the case of interest for our study), but recently the role of preferential sweeping has been extended to the case of wall-bounded turbulence (Bragg, Richter & Wang Reference Bragg, Richter and Wang2021a,Reference Bragg, Richter and Wangb). These studies have shown that, throughout much of the boundary layer, the preferential sweeping mechanism continues to play an important role. However, very close to the wall (e.g. in the buffer and viscous sublayers) where the turbulence inhomogeneity is strongest, the turbophoretic drift mechanism becomes the dominant mechanism responsible for enhancing the particle settling velocity.
$Fr$ dependence of the ‘multiscale preferential sweeping’ mechanism. It should also be noted that most of these studies focused on homogeneous turbulence (which is also the case of interest for our study), but recently the role of preferential sweeping has been extended to the case of wall-bounded turbulence (Bragg, Richter & Wang Reference Bragg, Richter and Wang2021a,Reference Bragg, Richter and Wangb). These studies have shown that, throughout much of the boundary layer, the preferential sweeping mechanism continues to play an important role. However, very close to the wall (e.g. in the buffer and viscous sublayers) where the turbulence inhomogeneity is strongest, the turbophoretic drift mechanism becomes the dominant mechanism responsible for enhancing the particle settling velocity.
As noted previously, except in restricted regimes, two-way coupling can also be important for how the inertial particles settle. It is commonly argued that the effects of 2WC are only important when the volume loading exceeds a certain threshold, e.g. when ![]() $\varPhi _v\geq 10^{-6}$. (Strictly speaking, it is
$\varPhi _v\geq 10^{-6}$. (Strictly speaking, it is ![]() $\varPhi _m$ that determines whether the effects of 2WC are important, not
$\varPhi _m$ that determines whether the effects of 2WC are important, not ![]() $\varPhi _v$. However, since they are proportional for a given
$\varPhi _v$. However, since they are proportional for a given ![]() $\rho _p/\rho _f$, then often the influence of the particles is discussed in terms of
$\rho _p/\rho _f$, then often the influence of the particles is discussed in terms of ![]() $\varPhi _v$.) For example, in Bosse, Kleiser & Meiburg (Reference Bosse, Kleiser and Meiburg2006) the fluid energy spectrums for 1WC and 2WC flows are almost identical for
$\varPhi _v$.) For example, in Bosse, Kleiser & Meiburg (Reference Bosse, Kleiser and Meiburg2006) the fluid energy spectrums for 1WC and 2WC flows are almost identical for ![]() $\varPhi _v = 10^{-5}$, but become noticeably different for
$\varPhi _v = 10^{-5}$, but become noticeably different for ![]() $\varPhi _v = 10^{-4}$. However, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) showed using DNS that, even when
$\varPhi _v = 10^{-4}$. However, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) showed using DNS that, even when ![]() $\varPhi _v$ was small enough such that the globally averaged fluid statistics are almost the same for the 1WC and 2WC cases, the average particle settling velocities were nevertheless very strongly modified due to 2WC. Their explanation was that even though
$\varPhi _v$ was small enough such that the globally averaged fluid statistics are almost the same for the 1WC and 2WC cases, the average particle settling velocities were nevertheless very strongly modified due to 2WC. Their explanation was that even though ![]() $\varPhi _v$ was too small for the inertial particles to significantly affect the global fluid statistics, 2WC can nevertheless strongly modify the flow statistics in the vicinity of the particles, which in turn affects the particle settling due to modifications of the drag force acting on the particles. Therefore, 2WC may be important for particle processes such as settling, in regimes where it was previously thought to be unimportant.
$\varPhi _v$ was too small for the inertial particles to significantly affect the global fluid statistics, 2WC can nevertheless strongly modify the flow statistics in the vicinity of the particles, which in turn affects the particle settling due to modifications of the drag force acting on the particles. Therefore, 2WC may be important for particle processes such as settling, in regimes where it was previously thought to be unimportant.
Concerning the mechanism responsible for enhanced particle settling in turbulent flows with 2WC, numerical simulations with 2WC (Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Monchaux & Dejoan Reference Monchaux and Dejoan2017) and laboratory experiments (Aliseda et al. Reference Aliseda, Cartellier, Hainaux and Lasheras2002; Good et al. Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014; Huck et al. Reference Huck, Bateson, Volk, Cartellier, Bourgoin and Aliseda2018; Petersen et al. Reference Petersen, Baker and Coletti2019) have shown that clusters of particles tend to fall faster than particles that are not part of a cluster. Huck et al. (Reference Huck, Bateson, Volk, Cartellier, Bourgoin and Aliseda2018) proposed different regimes affecting the settling velocity based on the local particle concentration by studying a polydisperse distribution of inertial particles in decaying turbulence. The settling velocity increases with both the local concentration and the area of the particle cluster, with collective effects generating downward forces on the high particle density regions (Aliseda et al. Reference Aliseda, Cartellier, Hainaux and Lasheras2002; Huck et al. Reference Huck, Bateson, Volk, Cartellier, Bourgoin and Aliseda2018). In particular, particles fall faster than average when the local particle number density is larger than ![]() $\approx$3 times the average number density. This is possibly consistent with the preferential sweeping effect since particle clusters would be expected to form in the same strain-dominated regions where the particles preferentially sample the downward moving fluid. However, it could also be the case that the settling is faster in these regions because 2WC allows the particle clusters to drag the surrounding fluid down with them, decreasing the drag resistance to their falling motion (Monchaux & Dejoan Reference Monchaux and Dejoan2017). Indeed, by considering the flow topology sampled by the settling particles, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) argued that as
$\approx$3 times the average number density. This is possibly consistent with the preferential sweeping effect since particle clusters would be expected to form in the same strain-dominated regions where the particles preferentially sample the downward moving fluid. However, it could also be the case that the settling is faster in these regions because 2WC allows the particle clusters to drag the surrounding fluid down with them, decreasing the drag resistance to their falling motion (Monchaux & Dejoan Reference Monchaux and Dejoan2017). Indeed, by considering the flow topology sampled by the settling particles, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) argued that as ![]() $\varPhi _m$ is increased, the preferential sweeping effect becomes less important, and the dragging of the fluid by the particle becomes the main mechanism associated with the enhanced particle settling velocities. It is also worth mentioning that exciting new field experiments have provided evidence for settling enhancement due to turbulence in diverse naturally occurring flows (Nemes et al. Reference Nemes, Dasari, Hong, Guala and Coletti2017; Li et al. Reference Li, Lim, Berk, Abraham, Heisel, Guala, Coletti and Hong2021a). Moreover, Li et al. (Reference Li, Abraham, Guala and Hong2021b) provided direct evidence that this enhancement is, in fact, associated with the preferential sweeping mechanism. Since these field experiments could be impacted by 2WC, the results may suggest that the preferential sweeping mechanism still applies in that regime.
$\varPhi _m$ is increased, the preferential sweeping effect becomes less important, and the dragging of the fluid by the particle becomes the main mechanism associated with the enhanced particle settling velocities. It is also worth mentioning that exciting new field experiments have provided evidence for settling enhancement due to turbulence in diverse naturally occurring flows (Nemes et al. Reference Nemes, Dasari, Hong, Guala and Coletti2017; Li et al. Reference Li, Lim, Berk, Abraham, Heisel, Guala, Coletti and Hong2021a). Moreover, Li et al. (Reference Li, Abraham, Guala and Hong2021b) provided direct evidence that this enhancement is, in fact, associated with the preferential sweeping mechanism. Since these field experiments could be impacted by 2WC, the results may suggest that the preferential sweeping mechanism still applies in that regime.
While the aforementioned studies point to an important role from 2WC in determining the particle settling speeds, a number of interesting and important issues remain to be solved. In Tom & Bragg (Reference Tom and Bragg2019), we used theory and DNS to reveal the truly multiscale character of the preferential sweeping mechanism, and the way in which a restricted range of turbulent eddies contributes to the preferential sweeping of an inertial particle, with the relevant range depending upon ![]() $\textit {St}$ and
$\textit {St}$ and ![]() $\textit {Sv}$. A natural and important question is how 2WC modifies this multiscale physical picture. It is precisely this question that we explore in the present paper, by extending the analysis of Tom & Bragg (Reference Tom and Bragg2019) to a system with 2WC. One important finding of our study is that it yields an alternative interpretation to that presented in Monchaux & Dejoan (Reference Monchaux and Dejoan2017) regarding the role of preferential sweeping in the presence of 2WC.
$\textit {Sv}$. A natural and important question is how 2WC modifies this multiscale physical picture. It is precisely this question that we explore in the present paper, by extending the analysis of Tom & Bragg (Reference Tom and Bragg2019) to a system with 2WC. One important finding of our study is that it yields an alternative interpretation to that presented in Monchaux & Dejoan (Reference Monchaux and Dejoan2017) regarding the role of preferential sweeping in the presence of 2WC.
The outline of the rest of the paper is as follows. In § 2 we summarize the theory of Tom & Bragg (Reference Tom and Bragg2019) and discuss its extension to 2WC flows. In § 3 we summarize the details of our DNS and the method used to capture 2WC. In § 4 we present and discuss the DNS results and explore various quantities in order to understand the role that 2WC plays in the enhancement of particle settling velocities due to turbulence and its impact on the preferential sweeping mechanism. Finally, in § 5 we draw conclusions to our work and mention important steps for future work.
2. Theory
2.1. Background
We consider the settling of small (![]() $d_p/\eta \ll 1$, where
$d_p/\eta \ll 1$, where ![]() $d_p$ is the particle diameter and
$d_p$ is the particle diameter and ![]() $\eta$ is the Kolmogorov length scale), heavy (
$\eta$ is the Kolmogorov length scale), heavy (![]() $\rho _p/\rho _f \gg 1$, where
$\rho _p/\rho _f \gg 1$, where ![]() $\rho _p$ is particle density and
$\rho _p$ is particle density and ![]() $\rho _f$ is fluid density), spherical, mono-disperse inertial particles in a statistically stationary, homogeneous (and initially isotropic) turbulent flow. In the regime of a linear drag force, the particle equation of motion reduces to (see Maxey & Riley Reference Maxey and Riley1983)
$\rho _f$ is fluid density), spherical, mono-disperse inertial particles in a statistically stationary, homogeneous (and initially isotropic) turbulent flow. In the regime of a linear drag force, the particle equation of motion reduces to (see Maxey & Riley Reference Maxey and Riley1983)
where ![]() $\boldsymbol {x}^p(t),\boldsymbol {v}^p(t)$ are the particle position and velocity vectors, respectively,
$\boldsymbol {x}^p(t),\boldsymbol {v}^p(t)$ are the particle position and velocity vectors, respectively, ![]() $\boldsymbol {u}(\boldsymbol {x}^p(t),t)$ is the undisturbed fluid velocity at the particle position and
$\boldsymbol {u}(\boldsymbol {x}^p(t),t)$ is the undisturbed fluid velocity at the particle position and ![]() $\boldsymbol {g}$ is the gravitational acceleration vector. Even though idealized, this simplified equation of motion is widely used for describing particle motion in atmospheric flows (e.g. Grabowski & Wang Reference Grabowski and Wang2013), and even for this equation of motion, many unanswered questions remain concerning the settling of particles in turbulence. Moreover, our DNS will be confined to
$\boldsymbol {g}$ is the gravitational acceleration vector. Even though idealized, this simplified equation of motion is widely used for describing particle motion in atmospheric flows (e.g. Grabowski & Wang Reference Grabowski and Wang2013), and even for this equation of motion, many unanswered questions remain concerning the settling of particles in turbulence. Moreover, our DNS will be confined to ![]() $St\leq 2$ and
$St\leq 2$ and ![]() $Sv\leq 2$ for which we expect that the linear drag approximation will be reasonable.
$Sv\leq 2$ for which we expect that the linear drag approximation will be reasonable.
In a 2WC system, a particle exerts a force on the fluid at its location equal to
which is equal and opposite to the drag force exerted by the fluid on the particles that is described by (2.1), and ![]() $m_p=(4/3){\rm \pi} (d_p/2)^3\rho _p$ is the mass of the spherical particle. The addition of the feedback force,
$m_p=(4/3){\rm \pi} (d_p/2)^3\rho _p$ is the mass of the spherical particle. The addition of the feedback force, ![]() $\boldsymbol {f}^p(t)$, breaks the isotropic symmetry of an otherwise isotropic turbulent flow, but the fluid is still statistically homogeneous since the gravitational body force is independent of position.
$\boldsymbol {f}^p(t)$, breaks the isotropic symmetry of an otherwise isotropic turbulent flow, but the fluid is still statistically homogeneous since the gravitational body force is independent of position.
Statistical stationarity of the system implies that, in the vertical direction defined by ![]() $\boldsymbol {e}_z$, the ensemble average of (2.1) is (with
$\boldsymbol {e}_z$, the ensemble average of (2.1) is (with ![]() $\boldsymbol {g}=-g\boldsymbol {e}_z$)
$\boldsymbol {g}=-g\boldsymbol {e}_z$)
Note that we used ![]() $\boldsymbol {g}=g\boldsymbol {e}_z$ in Tom & Bragg (Reference Tom and Bragg2019), but have decided to switch to this more standard choice of coordinate system in this paper. Equation (2.3) shows that the average particle velocity may differ from the Stokes settling velocity
$\boldsymbol {g}=g\boldsymbol {e}_z$ in Tom & Bragg (Reference Tom and Bragg2019), but have decided to switch to this more standard choice of coordinate system in this paper. Equation (2.3) shows that the average particle velocity may differ from the Stokes settling velocity ![]() $-St\,\tau _\eta {g}$ only if
$-St\,\tau _\eta {g}$ only if ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle \neq {0}$ (we consider flows with Eulerian average
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle \neq {0}$ (we consider flows with Eulerian average ![]() $\langle u_z(\boldsymbol {x},t)\rangle =0$, such that
$\langle u_z(\boldsymbol {x},t)\rangle =0$, such that ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle \neq {0}$ can only arise due to non-trivial effects in the flow). Several numerical studies for both 1WC (Wang & Maxey Reference Wang and Maxey1993; Bec et al. Reference Bec, Homann and Ray2014; Ireland et al. Reference Ireland, Bragg and Collins2016b; Rosa et al. Reference Rosa, Parishani, Ayala and Wang2016) and 2WC systems (Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Dejoan Reference Dejoan2011; Monchaux & Dejoan Reference Monchaux and Dejoan2017; Rosa et al. Reference Rosa, Kopeć, Ababaei and Pozorski2021) have indeed shown that
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle \neq {0}$ can only arise due to non-trivial effects in the flow). Several numerical studies for both 1WC (Wang & Maxey Reference Wang and Maxey1993; Bec et al. Reference Bec, Homann and Ray2014; Ireland et al. Reference Ireland, Bragg and Collins2016b; Rosa et al. Reference Rosa, Parishani, Ayala and Wang2016) and 2WC systems (Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Dejoan Reference Dejoan2011; Monchaux & Dejoan Reference Monchaux and Dejoan2017; Rosa et al. Reference Rosa, Kopeć, Ababaei and Pozorski2021) have indeed shown that ![]() $\langle {v}_z^p(t)\rangle \neq -St\,\tau _\eta {g}$, implying
$\langle {v}_z^p(t)\rangle \neq -St\,\tau _\eta {g}$, implying ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle \neq {0}$. Experimental studies in the laboratory (Aliseda et al. Reference Aliseda, Cartellier, Hainaux and Lasheras2002; Yang & Shy Reference Yang and Shy2005; Good et al. Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014; Petersen et al. Reference Petersen, Baker and Coletti2019) and more recently, settling velocity measurements in the atmosphere (Nemes et al. Reference Nemes, Dasari, Hong, Guala and Coletti2017; Li et al. Reference Li, Lim, Berk, Abraham, Heisel, Guala, Coletti and Hong2021a,Reference Li, Abraham, Guala and Hongb), both of which inherently have 2WC effects, have also observed an enhancement of settling velocity compared with the Stokes settling velocity. Hence, there is a need to explore the physical mechanism(s) responsible for generating
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle \neq {0}$. Experimental studies in the laboratory (Aliseda et al. Reference Aliseda, Cartellier, Hainaux and Lasheras2002; Yang & Shy Reference Yang and Shy2005; Good et al. Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014; Petersen et al. Reference Petersen, Baker and Coletti2019) and more recently, settling velocity measurements in the atmosphere (Nemes et al. Reference Nemes, Dasari, Hong, Guala and Coletti2017; Li et al. Reference Li, Lim, Berk, Abraham, Heisel, Guala, Coletti and Hong2021a,Reference Li, Abraham, Guala and Hongb), both of which inherently have 2WC effects, have also observed an enhancement of settling velocity compared with the Stokes settling velocity. Hence, there is a need to explore the physical mechanism(s) responsible for generating ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <{0}$ and whether there are different mechanisms at play for the 1WC and 2WC systems.
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <{0}$ and whether there are different mechanisms at play for the 1WC and 2WC systems.
2.2. Brief summary of the theoretical framework
For the 1WC system, Maxey (Reference Maxey1987) developed a theoretical framework to explain how ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <{0}$ can occur even in flows where the Eulerian flow average is
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <{0}$ can occur even in flows where the Eulerian flow average is ![]() $\langle {u}_z(\boldsymbol {x},t)\rangle ={0}$. Essentially, the explanation is that particles with inertia do not uniformly sample the underlying fluid velocity field, and that gravity leads to a bias for inertial particles to accumulate in regions of the flow where
$\langle {u}_z(\boldsymbol {x},t)\rangle ={0}$. Essentially, the explanation is that particles with inertia do not uniformly sample the underlying fluid velocity field, and that gravity leads to a bias for inertial particles to accumulate in regions of the flow where ![]() $\boldsymbol {e}_z\boldsymbol {\cdot } \boldsymbol {u}<0$. However, the analysis of Maxey (Reference Maxey1987) was restricted to
$\boldsymbol {e}_z\boldsymbol {\cdot } \boldsymbol {u}<0$. However, the analysis of Maxey (Reference Maxey1987) was restricted to ![]() $St\ll 1$. In a recent paper (Tom & Bragg Reference Tom and Bragg2019), we developed a theoretical framework for considering the behaviour of
$St\ll 1$. In a recent paper (Tom & Bragg Reference Tom and Bragg2019), we developed a theoretical framework for considering the behaviour of ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ for arbitrary
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ for arbitrary ![]() $St$, and for revealing the scales of motion that contribute to
$St$, and for revealing the scales of motion that contribute to ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ being finite and negative. Here, we briefly summarize the steps of the theoretical analysis and comment on how the analytical result can be used to understand how 2WC might modify the physical mechanisms governing the particle settling velocity.
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ being finite and negative. Here, we briefly summarize the steps of the theoretical analysis and comment on how the analytical result can be used to understand how 2WC might modify the physical mechanisms governing the particle settling velocity.
The key ideas used for developing the theoretical framework to analyse ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ for arbitrary
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ for arbitrary ![]() $St$ are averaging decompositions and probability density function (PDF) methods. The only assumptions made in our derivation are that the system is statistically stationary and homogeneous, and that the particle dynamics is governed by (2.1). The basic steps in the derivation are as follows (see Tom & Bragg Reference Tom and Bragg2019 for more details). For the system under consideration, an ensemble average
$St$ are averaging decompositions and probability density function (PDF) methods. The only assumptions made in our derivation are that the system is statistically stationary and homogeneous, and that the particle dynamics is governed by (2.1). The basic steps in the derivation are as follows (see Tom & Bragg Reference Tom and Bragg2019 for more details). For the system under consideration, an ensemble average ![]() $\langle\,\cdot\,\rangle$ over all possible states of the system corresponds to averaging over all realizations of
$\langle\,\cdot\,\rangle$ over all possible states of the system corresponds to averaging over all realizations of ![]() $\boldsymbol {u}$, as well as over all initial particle positions
$\boldsymbol {u}$, as well as over all initial particle positions ![]() $\boldsymbol {x}^p(0)=\boldsymbol {x}_0$ and velocities
$\boldsymbol {x}^p(0)=\boldsymbol {x}_0$ and velocities ![]() $\boldsymbol {v}^p(0)=\boldsymbol {v}_0$. In view of this, we introduce the averaging decomposition
$\boldsymbol {v}^p(0)=\boldsymbol {v}_0$. In view of this, we introduce the averaging decomposition ![]() $\langle\,\cdot\,\rangle =\langle \langle\,\cdot\,\rangle ^{\boldsymbol {x}_0,\boldsymbol {v}_0}_{\boldsymbol {u}}\rangle ^{\boldsymbol {u}}$ (Bragg, Swailes & Skartlien Reference Bragg, Swailes and Skartlien2012), where
$\langle\,\cdot\,\rangle =\langle \langle\,\cdot\,\rangle ^{\boldsymbol {x}_0,\boldsymbol {v}_0}_{\boldsymbol {u}}\rangle ^{\boldsymbol {u}}$ (Bragg, Swailes & Skartlien Reference Bragg, Swailes and Skartlien2012), where ![]() $\langle\,\cdot\,\rangle ^{\boldsymbol {x}_0,\boldsymbol {v}_0}_{\boldsymbol {u}}$ denotes an average over all initial particle positions
$\langle\,\cdot\,\rangle ^{\boldsymbol {x}_0,\boldsymbol {v}_0}_{\boldsymbol {u}}$ denotes an average over all initial particle positions ![]() $\boldsymbol {x}^p(0)=\boldsymbol {x}_0$ and velocities
$\boldsymbol {x}^p(0)=\boldsymbol {x}_0$ and velocities ![]() $\boldsymbol {v}^p(0)=\boldsymbol {v}_0$ for a given realization of the fluid velocity field
$\boldsymbol {v}^p(0)=\boldsymbol {v}_0$ for a given realization of the fluid velocity field ![]() $\boldsymbol {u}$, and
$\boldsymbol {u}$, and ![]() $\langle\,\cdot\,\rangle ^{\boldsymbol {u}}$ denotes an average over all realizations of
$\langle\,\cdot\,\rangle ^{\boldsymbol {u}}$ denotes an average over all realizations of ![]() $\boldsymbol {u}$. Using this operator, we construct a generalized particle velocity field
$\boldsymbol {u}$. Using this operator, we construct a generalized particle velocity field ![]() $\boldsymbol {\mathcal {V}}(\boldsymbol {x},t)\equiv \langle \boldsymbol {v}^p(t)\rangle ^{\boldsymbol {x}_0,\boldsymbol {v}_0}_{\boldsymbol {u}}$ that is well defined for all
$\boldsymbol {\mathcal {V}}(\boldsymbol {x},t)\equiv \langle \boldsymbol {v}^p(t)\rangle ^{\boldsymbol {x}_0,\boldsymbol {v}_0}_{\boldsymbol {u}}$ that is well defined for all ![]() $St$, including the regime where caustics occur (Wilkinson & Mehlig Reference Wilkinson and Mehlig2005) because it is formed by averaging over trajectories satisfying
$St$, including the regime where caustics occur (Wilkinson & Mehlig Reference Wilkinson and Mehlig2005) because it is formed by averaging over trajectories satisfying ![]() $\boldsymbol {x}^p(t)=\boldsymbol {x}$ (i.e. it does not assume uniqueness of these trajectories, a scenario that only applies in the limit
$\boldsymbol {x}^p(t)=\boldsymbol {x}$ (i.e. it does not assume uniqueness of these trajectories, a scenario that only applies in the limit ![]() $St\to 0$ that was considered in Maxey Reference Maxey1987). With this velocity field we then construct the result
$St\to 0$ that was considered in Maxey Reference Maxey1987). With this velocity field we then construct the result
where the notation ![]() $s\mid \boldsymbol {x},t$ denotes that the variable is measured at time
$s\mid \boldsymbol {x},t$ denotes that the variable is measured at time ![]() $s$ along a trajectory satisfying
$s$ along a trajectory satisfying ![]() $\boldsymbol {\mathcal {X}}(t)=\boldsymbol {x}$, and where
$\boldsymbol {\mathcal {X}}(t)=\boldsymbol {x}$, and where ![]() $\partial _s\boldsymbol {\mathcal {X}}\equiv \boldsymbol {\mathcal {V}}(\boldsymbol {\mathcal {X}}(s),s)$.
$\partial _s\boldsymbol {\mathcal {X}}\equiv \boldsymbol {\mathcal {V}}(\boldsymbol {\mathcal {X}}(s),s)$.
The result was further developed to gain insight into the multiscale nature of the problem by introducing coarse-graining decompositions ![]() $u_z(\boldsymbol {x},t)=\tilde {u}_z(\boldsymbol {x},t)+u'_z(\boldsymbol {x},t)$ and
$u_z(\boldsymbol {x},t)=\tilde {u}_z(\boldsymbol {x},t)+u'_z(\boldsymbol {x},t)$ and ![]() $\boldsymbol {\mathcal {V}}=\tilde {\boldsymbol {\mathcal {V}}}+\boldsymbol {\mathcal {V}}'$, where
$\boldsymbol {\mathcal {V}}=\tilde {\boldsymbol {\mathcal {V}}}+\boldsymbol {\mathcal {V}}'$, where ![]() $\tilde {u}_z$ and
$\tilde {u}_z$ and ![]() $\tilde {\boldsymbol {\mathcal {V}}}$ denote the fields
$\tilde {\boldsymbol {\mathcal {V}}}$ denote the fields ![]() $u_z$ and
$u_z$ and ![]() ${\boldsymbol {\mathcal {V}}}$ coarse grained on the length scale
${\boldsymbol {\mathcal {V}}}$ coarse grained on the length scale ![]() $\ell _c$, while
$\ell _c$, while ![]() $u'_z(\boldsymbol {x},t)\equiv u_z(\boldsymbol {x},t)-\tilde {u}_z(\boldsymbol {x},t)$ and
$u'_z(\boldsymbol {x},t)\equiv u_z(\boldsymbol {x},t)-\tilde {u}_z(\boldsymbol {x},t)$ and ![]() $\boldsymbol {\mathcal {V}}'\equiv \boldsymbol {\mathcal {V}}-\tilde {\boldsymbol {\mathcal {V}}}$ are the ‘sub-grid’ fields. Next, we choose
$\boldsymbol {\mathcal {V}}'\equiv \boldsymbol {\mathcal {V}}-\tilde {\boldsymbol {\mathcal {V}}}$ are the ‘sub-grid’ fields. Next, we choose ![]() $\ell _c$ to be a function of
$\ell _c$ to be a function of ![]() $\textit {St}$, i.e.
$\textit {St}$, i.e. ![]() $\ell _c(\textit {St})$, which is defined such that the scale-dependent Stokes number
$\ell _c(\textit {St})$, which is defined such that the scale-dependent Stokes number ![]() $St_{\ell }\equiv \tau _p/\tau _{\ell }$ (where
$St_{\ell }\equiv \tau _p/\tau _{\ell }$ (where ![]() $\tau _{\ell }$ is the eddy-turnover time scale at scale
$\tau _{\ell }$ is the eddy-turnover time scale at scale ![]() $\ell$) is
$\ell$) is ![]() $\lll 1$ for
$\lll 1$ for ![]() $\ell >\ell _c(St)$. Physically, this means that
$\ell >\ell _c(St)$. Physically, this means that ![]() $\ell _c(St)$ is defined to be the scale above which the particle behaves as if it were a fluid particle. Using this choice for the filtering length, we finally obtain
$\ell _c(St)$ is defined to be the scale above which the particle behaves as if it were a fluid particle. Using this choice for the filtering length, we finally obtain
Since the right-hand side of this result only contains the sub-grid fields, it shows that the turbulent flow scales that contribute to the enhanced particle settling speeds are those with size ![]() $<\ell _c$, while scales
$<\ell _c$, while scales ![]() $>\ell _c$ make a vanishingly small contribution. The physical mechanism embedded in (2.5) is a multiscale version of the original preferential sweeping mechanism described by Maxey (Reference Maxey1987) and Wang & Maxey (Reference Wang and Maxey1993). In particular, according to (2.5),
$>\ell _c$ make a vanishingly small contribution. The physical mechanism embedded in (2.5) is a multiscale version of the original preferential sweeping mechanism described by Maxey (Reference Maxey1987) and Wang & Maxey (Reference Wang and Maxey1993). In particular, according to (2.5), ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$ occurs because the inertial particles are preferentially swept by eddies of size
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$ occurs because the inertial particles are preferentially swept by eddies of size ![]() $\ell <\ell _c(St)$.
$\ell <\ell _c(St)$.
2.3. Applicability of theoretical analysis for the 2WC case
Although the result in (2.5) was derived for a 1WC system, its assumptions are such that it also applies in the 2WC regime. The only difference is one of interpretation, since in the 2WC case, all of the dynamical variables contained within (2.5) are implicitly affected by the force from the particle on the fluid. In view of this, we now consider how 2WC might affect the different quantities in (2.5) in order to understand the impact of 2WC on particle settling in turbulence.
The result in (2.5) shows that the settling modification due to turbulence associated with ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$ is determined by two things, namely the strength of the fluctuations of the sub-grid field
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$ is determined by two things, namely the strength of the fluctuations of the sub-grid field ![]() ${u}'_z(\boldsymbol {x},t)$, and the intensity of the particle clustering (associated with the exponential term involving the compressibility
${u}'_z(\boldsymbol {x},t)$, and the intensity of the particle clustering (associated with the exponential term involving the compressibility ![]() $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {V}}'$). It is to be noted, however, that as emphasized in Tom & Bragg (Reference Tom and Bragg2019), it is not merely the intensity of the clustering that matters but also whether it is correlated with
$\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {V}}'$). It is to be noted, however, that as emphasized in Tom & Bragg (Reference Tom and Bragg2019), it is not merely the intensity of the clustering that matters but also whether it is correlated with ![]() ${u}'_z(\boldsymbol {x},t)$. For example, in the 1WC case, unless the clustering is correlated with
${u}'_z(\boldsymbol {x},t)$. For example, in the 1WC case, unless the clustering is correlated with ![]() ${u}'_z(\boldsymbol {x},t)$ then the right-hand side of (2.5) is zero because
${u}'_z(\boldsymbol {x},t)$ then the right-hand side of (2.5) is zero because ![]() $\langle {u}'_z(\boldsymbol {x},t)\rangle ^{\boldsymbol {u}}=0$. For this reason, it is better to think of the exponential integral term in (2.5) as describing the process of preferential concentration rather than clustering, where preferential concentration describes how particles cluster preferentially in certain regions of the flow (see Bragg, Ireland & Collins (Reference Bragg, Ireland and Collins2015) for a discussion on the subtle differences between these phenomena).
$\langle {u}'_z(\boldsymbol {x},t)\rangle ^{\boldsymbol {u}}=0$. For this reason, it is better to think of the exponential integral term in (2.5) as describing the process of preferential concentration rather than clustering, where preferential concentration describes how particles cluster preferentially in certain regions of the flow (see Bragg, Ireland & Collins (Reference Bragg, Ireland and Collins2015) for a discussion on the subtle differences between these phenomena).
In the 1WC regime, the particles do not modify ![]() ${u}'_z(\boldsymbol {x},t)$. In the 2WC regime, the particles will modify
${u}'_z(\boldsymbol {x},t)$. In the 2WC regime, the particles will modify ![]() ${u}'_z(\boldsymbol {x},t)$, and previous results for non-settling particles have revealed a ‘pivoting effect’ wherein the inertial particles were observed to increase the energy content of turbulent flow scales of size less than some threshold, and decrease the energy content of flow scales larger than this (Elghobashi & Truesdell Reference Elghobashi and Truesdell1993; Sundaram & Collins Reference Sundaram and Collins1999; Bosse et al. Reference Bosse, Kleiser and Meiburg2006). The result in (2.5) shows that flow scales of size
${u}'_z(\boldsymbol {x},t)$, and previous results for non-settling particles have revealed a ‘pivoting effect’ wherein the inertial particles were observed to increase the energy content of turbulent flow scales of size less than some threshold, and decrease the energy content of flow scales larger than this (Elghobashi & Truesdell Reference Elghobashi and Truesdell1993; Sundaram & Collins Reference Sundaram and Collins1999; Bosse et al. Reference Bosse, Kleiser and Meiburg2006). The result in (2.5) shows that flow scales of size ![]() $\ell <\ell _c(St)$ contribute to the particle settling. The flows scales in the range
$\ell <\ell _c(St)$ contribute to the particle settling. The flows scales in the range ![]() $\ell <\ell _c(St)$ that dominate the settling will determine whether the pivoting mechanism tends to decrease or increase
$\ell <\ell _c(St)$ that dominate the settling will determine whether the pivoting mechanism tends to decrease or increase ![]() ${u}'_z(\boldsymbol {x},t)$. In the context of gravitational settling, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) argued that the settling particles can drag the fluid in their vicinity with them, an effect referred to as the ‘fluid-drag mechanism.’ This fluid drag mechanism could lead to an increase in the negative values of
${u}'_z(\boldsymbol {x},t)$. In the context of gravitational settling, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) argued that the settling particles can drag the fluid in their vicinity with them, an effect referred to as the ‘fluid-drag mechanism.’ This fluid drag mechanism could lead to an increase in the negative values of ![]() ${u}'_z(\boldsymbol {x},t)$ responsible for generating
${u}'_z(\boldsymbol {x},t)$ responsible for generating ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$. In such a case, 2WC could enhance the particle settling speeds.
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$. In such a case, 2WC could enhance the particle settling speeds.
2WC can also, however, modify the preferential concentration of the particles associated with the contribution ![]() $\exp (-\int _0^t\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {V}}'(\boldsymbol {\mathcal {X}}(s\mid \boldsymbol {x},t),s)\,{\rm d}s)$ in (2.5). It is more difficult to predict theoretically how 2WC might affect this contribution to (2.5), however, this is something that we can explore using DNS. It is important to note, however, that in a 2WC system, enhanced settling could occur even in the absence of preferential concentration. For example, even if
$\exp (-\int _0^t\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {V}}'(\boldsymbol {\mathcal {X}}(s\mid \boldsymbol {x},t),s)\,{\rm d}s)$ in (2.5). It is more difficult to predict theoretically how 2WC might affect this contribution to (2.5), however, this is something that we can explore using DNS. It is important to note, however, that in a 2WC system, enhanced settling could occur even in the absence of preferential concentration. For example, even if ![]() $\exp ( -\int _0^t\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {V}}'(\boldsymbol {\mathcal {X}}(s\mid \boldsymbol {x},t),s)\,{\rm d}s)= 1$ for all
$\exp ( -\int _0^t\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {V}}'(\boldsymbol {\mathcal {X}}(s\mid \boldsymbol {x},t),s)\,{\rm d}s)= 1$ for all ![]() $\boldsymbol {x}^p(t)=\boldsymbol {x}$, then we would have
$\boldsymbol {x}^p(t)=\boldsymbol {x}$, then we would have
where ![]() $\boldsymbol {y}$ corresponds to the homogeneous distribution of points in space where the particles are located. Although in a 1WC system
$\boldsymbol {y}$ corresponds to the homogeneous distribution of points in space where the particles are located. Although in a 1WC system ![]() $\langle {u}'_z(\boldsymbol {y},t)\rangle ^{\boldsymbol {u}}=0$, in a 2WC system we could have
$\langle {u}'_z(\boldsymbol {y},t)\rangle ^{\boldsymbol {u}}=0$, in a 2WC system we could have ![]() $\langle {u}'_z(\boldsymbol {y},t)\rangle ^{\boldsymbol {u}}<0$ and hence
$\langle {u}'_z(\boldsymbol {y},t)\rangle ^{\boldsymbol {u}}<0$ and hence ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$ due to the settling particles dragging the fluid down with them. In such a scenario the preferential sweeping mechanism would be playing no role. Measuring preferential concentration in the flow can therefore be used to indirectly determine whether
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$ due to the settling particles dragging the fluid down with them. In such a scenario the preferential sweeping mechanism would be playing no role. Measuring preferential concentration in the flow can therefore be used to indirectly determine whether ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$ in a 2WC system is due to preferential sweeping or not.
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle <0$ in a 2WC system is due to preferential sweeping or not.
It is also important to point out that, according to its definition, ![]() $\ell _c(St)$ will be the same for the 1WC and 2WC cases. To see this, we note that for point particles, the flow modification through 2WC is only possible due to particle inertia, and at any scale
$\ell _c(St)$ will be the same for the 1WC and 2WC cases. To see this, we note that for point particles, the flow modification through 2WC is only possible due to particle inertia, and at any scale ![]() $\ell$, the role of particle inertia can be quantified using
$\ell$, the role of particle inertia can be quantified using ![]() $St_\ell$. Since
$St_\ell$. Since ![]() $\ell _c(St)$ is defined as the scale above which
$\ell _c(St)$ is defined as the scale above which ![]() $St_\ell$ is so small that particle inertia can be ignored entirely, then this must also be the scale above which the effects of 2WC vanish, since at scales
$St_\ell$ is so small that particle inertia can be ignored entirely, then this must also be the scale above which the effects of 2WC vanish, since at scales ![]() $\ell >\ell _c(St)$, the inertial particles behave as if they were fluid particles, which by definition do not modify the flow.
$\ell >\ell _c(St)$, the inertial particles behave as if they were fluid particles, which by definition do not modify the flow.
In our previous work (Tom & Bragg Reference Tom and Bragg2019), we studied the contributions of different flow scales to the settling velocity enhancement in a 1WC system. In this work, we aim to extend this analysis to the 2WC regime. First, we will look at the effect of 2WC on the overall settling velocity enhancement, i.e. the contribution of all the flow scales to ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$. Second, we will study the effect of 2WC at different scales and also look at the relative contribution of different scales to the overall settling velocity enhancement. Third, we will analyse the effect of the two contributions embedded in (2.5) that affects settling velocity at different scales and investigate how these are modified by 2WC at different scales of the flow. Thus, we aim to elucidate how 2WC modifies the multiscale preferential sweeping mechanism.
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$. Second, we will study the effect of 2WC at different scales and also look at the relative contribution of different scales to the overall settling velocity enhancement. Third, we will analyse the effect of the two contributions embedded in (2.5) that affects settling velocity at different scales and investigate how these are modified by 2WC at different scales of the flow. Thus, we aim to elucidate how 2WC modifies the multiscale preferential sweeping mechanism.
3. Direct numerical simulations
We simulate numerically a homogeneous turbulent flow laden with settling inertial particles. The fluid flow is discretized on a Cartesian grid through an Eulerian approach, while a Lagrangian particle tracking approach is used for the particles. For consistency, the same point-particle equation of motion (2.1) is used as in the theory, and a major numerical challenge is to couple the fluid and particulate phases through their momentum exchange.
3.1. Fluid solver
We solve the three-dimensional, incompressible Navier–Stokes equation in rotational form
using the HiPPSTR code (Ireland et al. Reference Ireland, Vaithianathan, Sukheswalla, Ray and Collins2013), modified to account for the particle feedback on the flow ![]() $\boldsymbol {C}$. Here,
$\boldsymbol {C}$. Here, ![]() $\boldsymbol {\omega }\equiv \boldsymbol {\nabla }\times \boldsymbol {u}$ is the vorticity,
$\boldsymbol {\omega }\equiv \boldsymbol {\nabla }\times \boldsymbol {u}$ is the vorticity, ![]() $P$ is the pressure,
$P$ is the pressure, ![]() $\rho _f$ is the constant density of the fluid,
$\rho _f$ is the constant density of the fluid, ![]() $\nu$ is the kinematic viscosity,
$\nu$ is the kinematic viscosity, ![]() $\boldsymbol {f}$ is a large-scale forcing and
$\boldsymbol {f}$ is a large-scale forcing and ![]() $\boldsymbol {C}$ is the force exerted by the particles on the fluid. The spatial derivatives in (3.1) are discretized through a Fourier pseudo-spectral method. The nonlinearity introduces an aliasing error that is removed by using a combination of spherical truncation and phase shifting. The pressure gradient compensates the divergence of both the nonlinear convective term and the divergence of
$\boldsymbol {C}$ is the force exerted by the particles on the fluid. The spatial derivatives in (3.1) are discretized through a Fourier pseudo-spectral method. The nonlinearity introduces an aliasing error that is removed by using a combination of spherical truncation and phase shifting. The pressure gradient compensates the divergence of both the nonlinear convective term and the divergence of ![]() $\boldsymbol {C}$, thus yielding a solenoidal fluid velocity field. The Fourier modes are evolved in time by means of a second-order Runge–Kutta scheme with exponential integration for the viscous stress. A large-scale deterministic forcing scheme is applied at wavenumbers with magnitude
$\boldsymbol {C}$, thus yielding a solenoidal fluid velocity field. The Fourier modes are evolved in time by means of a second-order Runge–Kutta scheme with exponential integration for the viscous stress. A large-scale deterministic forcing scheme is applied at wavenumbers with magnitude ![]() $\kappa \leq \sqrt {2}$ that maintains a constant kinetic energy of the flow.
$\kappa \leq \sqrt {2}$ that maintains a constant kinetic energy of the flow.
3.2. Particle solver
The particle position and velocity are evolved using (2.1), with the fluid velocity at the particle position computed through B-spline interpolation (van Hinsberg et al. Reference van Hinsberg, Thije Boonkkamp, Toschi and Clercx2012; Carbone & Iovieno Reference Carbone and Iovieno2018; Mirigaldi, Carbone & Perrone Reference Mirigaldi, Carbone and Perrone2021). This operation is understood as a backward non-uniform fast Fourier transform (NUFFT) with B-spline basis (Beylkin Reference Beylkin1995). The fluid velocity field is projected onto the B-spline basis in Fourier space, then brought back to physical space by means of an inverse fast Fourier transform (FFT). Finally, this projected velocity field is interpolated at the particle position. We employed B-spline polynomials of order seven, which uses eight points for interpolation along each direction and has ![]() $C^6$ continuity (Ireland, Bragg & Collins Reference Ireland, Bragg and Collins2016a). The particles position and velocity are then evolved in time by means of an exponential integrator (Hochbruck & Ostermann Reference Hochbruck and Ostermann2010), that guarantees stability and accuracy even for very low Stokes numbers. For a more complete description of the DNS solver see Ireland et al. (Reference Ireland, Vaithianathan, Sukheswalla, Ray and Collins2013). Note, however, that in the current version of the HiPPSTR code used to simulate the 2WC system, the same exponential integration scheme is used for time advancement of both the fluid and particle solvers (unlike the original HiPPSTR code which used exponential integrators only for the particles), to ensure consistency between the handling of the two phases.
$C^6$ continuity (Ireland, Bragg & Collins Reference Ireland, Bragg and Collins2016a). The particles position and velocity are then evolved in time by means of an exponential integrator (Hochbruck & Ostermann Reference Hochbruck and Ostermann2010), that guarantees stability and accuracy even for very low Stokes numbers. For a more complete description of the DNS solver see Ireland et al. (Reference Ireland, Vaithianathan, Sukheswalla, Ray and Collins2013). Note, however, that in the current version of the HiPPSTR code used to simulate the 2WC system, the same exponential integration scheme is used for time advancement of both the fluid and particle solvers (unlike the original HiPPSTR code which used exponential integrators only for the particles), to ensure consistency between the handling of the two phases.
3.3. Flow parameters
The particles simulated are monodisperse, having the same radius and density. In order to be able to compare our results with those of Monchaux & Dejoan (Reference Monchaux and Dejoan2017) we use the same density ratio that they employed, i.e. ![]() $\rho _p/\rho _f=5000$, the same Froude number,
$\rho _p/\rho _f=5000$, the same Froude number, ![]() $\textit {Fr}=1$ and the same volume fraction,
$\textit {Fr}=1$ and the same volume fraction, ![]() $\varPhi _v=1.5\times 10^{-5}$, corresponding to a mass fraction
$\varPhi _v=1.5\times 10^{-5}$, corresponding to a mass fraction ![]() $\varPhi _m= 0.075$. We consider Stokes numbers
$\varPhi _m= 0.075$. We consider Stokes numbers ![]() $\textit {St}=0.3$, 0.5, 0.7, 1, 2 in order to explore the behaviour in the regimes of weak to moderate inertia. With these values of
$\textit {St}=0.3$, 0.5, 0.7, 1, 2 in order to explore the behaviour in the regimes of weak to moderate inertia. With these values of ![]() $\textit {Fr}$ and
$\textit {Fr}$ and ![]() $\textit {St}$, the artificial periodicity effects discussed in Ireland et al. (Reference Ireland, Bragg and Collins2016b) do not arise, thus avoiding the need to use very large flow domains in the direction of gravity.
$\textit {St}$, the artificial periodicity effects discussed in Ireland et al. (Reference Ireland, Bragg and Collins2016b) do not arise, thus avoiding the need to use very large flow domains in the direction of gravity.
It is also desirable to consider the effects of the Taylor Reynolds number ![]() $Re_\lambda$ on the flow, since as shown in Tom & Bragg (Reference Tom and Bragg2019), the range of scales in the flow is of crucial importance in determining the particle settling behaviour via the multiscale preferential sweeping mechanism. We found that it was necessary to run the DNS for very long times, of the order of 100 eddy-turnover times in order for the average vertical velocities of the particles to statistically converge, and this is similar to the convergence times reported in Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Rosa et al. (Reference Rosa, Parishani, Ayala and Wang2016). This then places severe limitations on the
$Re_\lambda$ on the flow, since as shown in Tom & Bragg (Reference Tom and Bragg2019), the range of scales in the flow is of crucial importance in determining the particle settling behaviour via the multiscale preferential sweeping mechanism. We found that it was necessary to run the DNS for very long times, of the order of 100 eddy-turnover times in order for the average vertical velocities of the particles to statistically converge, and this is similar to the convergence times reported in Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Rosa et al. (Reference Rosa, Parishani, Ayala and Wang2016). This then places severe limitations on the ![]() $Re_\lambda$ that can be simulated (due to limited computational resources), and as a result, we considered the range
$Re_\lambda$ that can be simulated (due to limited computational resources), and as a result, we considered the range ![]() $Re_\lambda \in [31,142]$. Although this range is too small to observe how the settling process might approach an asymptotic state with increasing
$Re_\lambda \in [31,142]$. Although this range is too small to observe how the settling process might approach an asymptotic state with increasing ![]() $Re_\lambda$ for sufficiently large
$Re_\lambda$ for sufficiently large ![]() $Re_\lambda$ (as suggested in Tom & Bragg Reference Tom and Bragg2019), it will nevertheless be shown to be sufficient to reveal significant effects of
$Re_\lambda$ (as suggested in Tom & Bragg Reference Tom and Bragg2019), it will nevertheless be shown to be sufficient to reveal significant effects of ![]() $Re_\lambda$ on the settling process.
$Re_\lambda$ on the settling process.
3.4. Two-way coupling
In the framework of the point-particle model, the force from the particles on the fluid is a superposition of Dirac delta functions centred at the particle position
 \begin{equation} \boldsymbol{C}(\boldsymbol{x},t) = \frac{L^3}{N_p}\varPhi_m \sum_p \frac{\boldsymbol{v}^p(t) - \boldsymbol{u}(\boldsymbol{x}^p,t)}{\tau_p} \delta(\boldsymbol{x} - \boldsymbol{x}^p(t)). \end{equation}
\begin{equation} \boldsymbol{C}(\boldsymbol{x},t) = \frac{L^3}{N_p}\varPhi_m \sum_p \frac{\boldsymbol{v}^p(t) - \boldsymbol{u}(\boldsymbol{x}^p,t)}{\tau_p} \delta(\boldsymbol{x} - \boldsymbol{x}^p(t)). \end{equation}
Note that, in this term, only the drag force on the particle is accounted for and not the gravitational body force experienced by the particle, as was also done in previous works (e.g. Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Monchaux & Dejoan Reference Monchaux and Dejoan2017). The reason for this is that this term is supposed to be equal and opposite to the force that the fluid applies to the particles located at ![]() $\boldsymbol {x}$, and the latter is associated with the hydrodynamic stresses on the particle surfaces (represented by the drag force in the point-particle model being used) and not with the gravitational body force.
$\boldsymbol {x}$, and the latter is associated with the hydrodynamic stresses on the particle surfaces (represented by the drag force in the point-particle model being used) and not with the gravitational body force.
The Fourier transform of (3.2) needed by the pseudo-spectral solver for the fluid phase is computed by means of the forward NUFFT with B-spline basis (Beylkin Reference Beylkin1995; Carbone & Iovieno Reference Carbone and Iovieno2018; Carbone, Bragg & Iovieno Reference Carbone, Bragg and Iovieno2019). This is motivated by the fact that a FFT is not directly applicable to (3.2), while a direct discrete Fourier transform would be computationally too expensive. A detailed description of the NUFFT algorithm for particles in turbulence can be found in Carbone & Iovieno (Reference Carbone and Iovieno2018, Reference Carbone and Iovieno2020). Briefly, the algorithm can be summarized through the equation
where ![]() $\mathcal {F}$ indicates the Fourier transform,
$\mathcal {F}$ indicates the Fourier transform, ![]() $*$ denotes a convolution, and
$*$ denotes a convolution, and ![]() $B_n$ is the B-spline polynomial of order
$B_n$ is the B-spline polynomial of order ![]() $n$.
$n$.
The B-spline polynomials are piecewise polynomial functions with compact support, usually defined as the inverse Fourier transform of powers of the sinc function. The zeroth-degree B-spline consists of a box function,
 \begin{equation} B_0(\boldsymbol{x}) =\begin{cases} 1/\Delta x, & -\Delta x/2 < x_i<{+}\Delta x/2 \\ 0, & \textrm{otherwise} \end{cases} \end{equation}
\begin{equation} B_0(\boldsymbol{x}) =\begin{cases} 1/\Delta x, & -\Delta x/2 < x_i<{+}\Delta x/2 \\ 0, & \textrm{otherwise} \end{cases} \end{equation}
and higher-order B-splines are obtained by taking recursive convolutions with ![]() $B_0$, namely
$B_0$, namely ![]() $B_{n+1}=B_n*B_0$. These B-spline polynomials guarantee high-accuracy interpolation (Beylkin Reference Beylkin1995) and are efficient for algorithm parallelization purposes (Carbone & Iovieno Reference Carbone and Iovieno2018, Reference Carbone and Iovieno2020).
$B_{n+1}=B_n*B_0$. These B-spline polynomials guarantee high-accuracy interpolation (Beylkin Reference Beylkin1995) and are efficient for algorithm parallelization purposes (Carbone & Iovieno Reference Carbone and Iovieno2018, Reference Carbone and Iovieno2020).
For an ideal computational grid with infinitely many grid points, (3.3) is just a tautology following from the convolution theorem. However, for a finite grid resolution, it is of great use in aiding the numerical implementation of a FFT of the field ![]() $\boldsymbol {C}$, consisting of a superposition of Dirac delta functions. In our implementation, we first compute the numerator of the right-hand side of (3.3), computing the convolution of
$\boldsymbol {C}$, consisting of a superposition of Dirac delta functions. In our implementation, we first compute the numerator of the right-hand side of (3.3), computing the convolution of ![]() $\boldsymbol {C}$ with
$\boldsymbol {C}$ with ![]() $B_n$ in physical space, thus spreading the field over the
$B_n$ in physical space, thus spreading the field over the ![]() $n+1$ adjacent grid points in each direction. This convolution procedure introduces a strong (artificial) non-locality, and the resulting field depends sensitively on the details of the smoothing function. The smoothed coupling field
$n+1$ adjacent grid points in each direction. This convolution procedure introduces a strong (artificial) non-locality, and the resulting field depends sensitively on the details of the smoothing function. The smoothed coupling field ![]() $\boldsymbol {C}*B_n$ can be accurately represented on the structured Cartesian grid, and it is then transformed to Fourier space by means of a standard FFT. Crucially, in the NUFFT algorithm the artificial spreading and non-locality introduced by the convolution
$\boldsymbol {C}*B_n$ can be accurately represented on the structured Cartesian grid, and it is then transformed to Fourier space by means of a standard FFT. Crucially, in the NUFFT algorithm the artificial spreading and non-locality introduced by the convolution ![]() $\mathcal {F}[\boldsymbol {C}*B_n]$ is subsequently removed in Fourier space by dividing by
$\mathcal {F}[\boldsymbol {C}*B_n]$ is subsequently removed in Fourier space by dividing by ![]() $\mathcal {F}[B_n]$, as shown in (3.3). The way in which this operation works can be easily understood as follows. A convolution (spreading) in physical space corresponds to multiplication in Fourier space, so that dividing by the Fourier transform of the B-spline amounts to taking an inverse convolution. Therefore, the smoothing is introduced only for numerical convenience as an intermediate step, and the outcome of the NUFFT calculation depends very weakly on the details of the kernel employed for convolution (Beylkin Reference Beylkin1995; Mirigaldi Reference Mirigaldi, Carbone and Perrone2021), the dependence being weaker as the number of grid points in the support of the kernel increases.
$\mathcal {F}[B_n]$, as shown in (3.3). The way in which this operation works can be easily understood as follows. A convolution (spreading) in physical space corresponds to multiplication in Fourier space, so that dividing by the Fourier transform of the B-spline amounts to taking an inverse convolution. Therefore, the smoothing is introduced only for numerical convenience as an intermediate step, and the outcome of the NUFFT calculation depends very weakly on the details of the kernel employed for convolution (Beylkin Reference Beylkin1995; Mirigaldi Reference Mirigaldi, Carbone and Perrone2021), the dependence being weaker as the number of grid points in the support of the kernel increases.
The NUFFT is a well-established algorithm in optics (Mirigaldi Reference Mirigaldi, Carbone and Perrone2021) and has been recently used to investigate the thermal coupling between a passive temperature field and inertial particles (Carbone et al. Reference Carbone, Bragg and Iovieno2019), and the results presented in this work have been crosschecked with the results from the code used in Carbone et al. (Reference Carbone, Bragg and Iovieno2019).
Most previous works used tri-linear extrapolation to distribute the contribution of the particle on the nearest grid points (Bosse et al. Reference Bosse, Kleiser and Meiburg2006). One of the main reasons for this choice is that a low-order polynomial reduces the artificial non-localities that arise due to spreading the effect of the particle momentum onto the surrounding grid points. In the NUFFT, the initial convolution in physical space is subsequently removed in Fourier space, so that the method does not suffer from the artificial non-locality issues, which is a major advantage of the method. As a consequence, this approach allows to use higher-order B-spline polynomials to obtain a more accurate representation of the Dirac delta functions in (3.2). Moreover, many recent works (e.g. Rosa et al. Reference Rosa, Kopeć, Ababaei and Pozorski2021) used high-order schemes for the interpolation of the fluid velocity at the particle position combined with low-order schemes for the computation of the coupling term. Since this introduces errors in the energy balance of the system (Sundaram & Collins Reference Sundaram and Collins1996), we employ the same B-spline polynomial basis of degree 7 (that uses 8 points in each direction) for interpolation of the velocity field and computation of the coupling term ![]() $\boldsymbol {C}$.
$\boldsymbol {C}$.
3.5. Numerical considerations
Within the context of the point-particle model, our simulations ignore the effects of the Basset history force, the Faxen curvature corrections, the pressure gradient and added mass contributions that appear in the full form of the equation derived in Maxey & Riley (Reference Maxey and Riley1983). However, the neglect of these terms is well justified for the particle sizes and densities being studied here (Daitche Reference Daitche2015). We also do not consider nonlinear drag corrections since our DNS are confined to the portion of the parameter range where a linear drag coefficient is a reasonable approximation.
With respect to the point-particle approach itself, it is known that for some parameter regimes the method has significant limitations (Eaton Reference Eaton2009; Balachandar & Eaton Reference Balachandar and Eaton2010; Brandt & Coletti Reference Brandt and Coletti2022). Only particle-resolved DNS allows for capturing all the flow details in the vicinity of the particles, and thereby overcoming the limitations of point-particle models (Vreman Reference Vreman2016). However, particle-resolved simulations are computationally extremely expensive for particles with ![]() $d_p\ll \eta$, and in view of this a point-particle approach is often used as an optimum choice (Brandt & Coletti Reference Brandt and Coletti2022). Moreover, in at least some parameter regimes, the point-particle approach should be valid provided that
$d_p\ll \eta$, and in view of this a point-particle approach is often used as an optimum choice (Brandt & Coletti Reference Brandt and Coletti2022). Moreover, in at least some parameter regimes, the point-particle approach should be valid provided that ![]() $d_p\ll \Delta x$ is satisfied and that the flow around the particle does in fact satisfy Stokes flow. However, we currently lack careful and extensive comparisons between point-particle DNS and experiments that would reveal exactly the parameter regimes for which the point-particle approach is valid (Petersen et al. Reference Petersen, Baker and Coletti2019; Brandt & Coletti Reference Brandt and Coletti2022). Hence, our DNS results which are based on the point-particle approach are to be placed within the context of the potential limitations of this modelling approach. But, as emphasized in § 2.1, this simple point-particle model is still widely used for describing particle motion in atmospheric flows (Grabowski & Wang Reference Grabowski and Wang2013), and even for particle motion governed by this simple model there remain many aspects that are not well understood. This again motivates the use of a point-particle model, before additional complexities such as finite particle size effects are introduced.
$d_p\ll \Delta x$ is satisfied and that the flow around the particle does in fact satisfy Stokes flow. However, we currently lack careful and extensive comparisons between point-particle DNS and experiments that would reveal exactly the parameter regimes for which the point-particle approach is valid (Petersen et al. Reference Petersen, Baker and Coletti2019; Brandt & Coletti Reference Brandt and Coletti2022). Hence, our DNS results which are based on the point-particle approach are to be placed within the context of the potential limitations of this modelling approach. But, as emphasized in § 2.1, this simple point-particle model is still widely used for describing particle motion in atmospheric flows (Grabowski & Wang Reference Grabowski and Wang2013), and even for particle motion governed by this simple model there remain many aspects that are not well understood. This again motivates the use of a point-particle model, before additional complexities such as finite particle size effects are introduced.
In the particle equation of motion (2.1), ![]() $\boldsymbol {u}(\boldsymbol {x}^p(t),t)$ is the undisturbed fluid velocity at the particle position, meaning the fluid velocity that does not include the disturbance of the particle under consideration (but can include the disturbance from all other particles in the flow). As a result, simply interpolating the fluid velocities from the surrounding grid points to evaluate
$\boldsymbol {u}(\boldsymbol {x}^p(t),t)$ is the undisturbed fluid velocity at the particle position, meaning the fluid velocity that does not include the disturbance of the particle under consideration (but can include the disturbance from all other particles in the flow). As a result, simply interpolating the fluid velocities from the surrounding grid points to evaluate ![]() $\boldsymbol {u}(\boldsymbol {x}^p(t),t)$ introduces an error because the interpolated velocities include the disturbance effect of the particle under consideration. This error can be significant for particles of size comparable to the grid spacing employed in the numerical simulation, i.e. when
$\boldsymbol {u}(\boldsymbol {x}^p(t),t)$ introduces an error because the interpolated velocities include the disturbance effect of the particle under consideration. This error can be significant for particles of size comparable to the grid spacing employed in the numerical simulation, i.e. when ![]() $d_p=O(\Delta x)$ (Boivin, Simonin & Squires Reference Boivin, Simonin and Squires1998). Moreover, this issue is particularly evident for particles settling in turbulence, and even in a still fluid (Horwitz & Mani Reference Horwitz and Mani2020). Correction schemes have been recently developed to approximately remove this error by providing a way to retrieve the undisturbed fluid velocity (Horwitz & Mani Reference Horwitz and Mani2018). However, in the regime
$d_p=O(\Delta x)$ (Boivin, Simonin & Squires Reference Boivin, Simonin and Squires1998). Moreover, this issue is particularly evident for particles settling in turbulence, and even in a still fluid (Horwitz & Mani Reference Horwitz and Mani2020). Correction schemes have been recently developed to approximately remove this error by providing a way to retrieve the undisturbed fluid velocity (Horwitz & Mani Reference Horwitz and Mani2018). However, in the regime ![]() $d_p\ll \Delta x$ the error will be small, and in our simulations
$d_p\ll \Delta x$ the error will be small, and in our simulations ![]() $d_p/\Delta x \leq 0.05$. As a result, a correction scheme is not required, and we simply evaluate
$d_p/\Delta x \leq 0.05$. As a result, a correction scheme is not required, and we simply evaluate ![]() $\boldsymbol {u}(\boldsymbol {x}^p(t),t)$ in (2.1) by interpolating the fluid velocities at the surrounding grid point to the particle position, as described earlier.
$\boldsymbol {u}(\boldsymbol {x}^p(t),t)$ in (2.1) by interpolating the fluid velocities at the surrounding grid point to the particle position, as described earlier.
The numerical resolution of DNS is usually quantified by ![]() $k_{max} \eta$, and the resolution of our DNS (
$k_{max} \eta$, and the resolution of our DNS (![]() $k_{max} \eta \approx 1.5$) is similar to or slightly better than the works of Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Monchaux & Dejoan (Reference Monchaux and Dejoan2017) against which compare our results. Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) used
$k_{max} \eta \approx 1.5$) is similar to or slightly better than the works of Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Monchaux & Dejoan (Reference Monchaux and Dejoan2017) against which compare our results. Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) used ![]() $k_{max} \eta \approx 1.29\unicode{x2013}1.55$ (see tables I and III) and Monchaux & Dejoan (Reference Monchaux and Dejoan2017) used
$k_{max} \eta \approx 1.29\unicode{x2013}1.55$ (see tables I and III) and Monchaux & Dejoan (Reference Monchaux and Dejoan2017) used ![]() $k_{max} \eta \approx 1.32$ (see table 1). While higher resolution might be required to capture intermittent events, our study focuses on first- and second-order moments and these are not very sensitive to intermittent events. Furthermore, if we were to increase the resolution of our DNS by reducing the grid spacing (for a given
$k_{max} \eta \approx 1.32$ (see table 1). While higher resolution might be required to capture intermittent events, our study focuses on first- and second-order moments and these are not very sensitive to intermittent events. Furthermore, if we were to increase the resolution of our DNS by reducing the grid spacing (for a given ![]() $St$ and
$St$ and ![]() $\varPhi _v$), then
$\varPhi _v$), then ![]() $d_p/\Delta x$ would enter the range where we would have to apply corrections to the fluid velocity in the particle equation of motion (Horwitz & Mani Reference Horwitz and Mani2018), and as mentioned above, this would add to the computational cost of the simulations. Hence, the current resolution is an optimal choice for tackling the questions we are trying to address in this work and for the parameter choices considered here, with reasonable computational resources.
$d_p/\Delta x$ would enter the range where we would have to apply corrections to the fluid velocity in the particle equation of motion (Horwitz & Mani Reference Horwitz and Mani2018), and as mentioned above, this would add to the computational cost of the simulations. Hence, the current resolution is an optimal choice for tackling the questions we are trying to address in this work and for the parameter choices considered here, with reasonable computational resources.
Finally, following previous works (Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Monchaux & Dejoan Reference Monchaux and Dejoan2017; Rosa et al. Reference Rosa, Kopeć, Ababaei and Pozorski2021), at each time step we set to zero the average fluid velocity in the direction of gravity. This is equivalent to applying a mean vertical pressure gradient (Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Monchaux & Dejoan Reference Monchaux and Dejoan2017; Rosa et al. Reference Rosa, Kopeć, Ababaei and Pozorski2021) without which the total kinetic energy in the flow would grow without bound due to the finite settling velocity of the particles continuously injecting kinetic energy into the flow. While introduced in Maxey & Patel (Reference Maxey and Patel2001) and used for 2WC simulations by Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) to remedy the numerical issue that arises for an unbounded flow, its physical validity could be called into question. However, a possible justification can be given as follows. Suppose one is considering the settling of heavy particles through a fully developed wall-bounded turbulent flow with 2WC at distances from the wall where the flow is quasi-homogeneous. In this case, although the settling particles will continuously force the flow in the vertical direction as they fall, the impermeability of the wall prevents a mean flow from developing in this direction, and this effect is mediated to the upper, quasi-homogeneous region of the flow through the mean forces in the fluid. Hence in this situation, the settling particles would not generate a mean flow as they settle (although the mean fluid velocity evaluated at the particle positions can still be finite, and indeed will be if the flow modifies the particle settling velocity compared with the Stokes settling velocity). This potential justification is also hinted at in Maxey & Patel (Reference Maxey and Patel2001). In addition to this potential justification, we also use this aforementioned method of enforcing a zero mean fluid velocity at each time step in order to be able to meaningfully compare our results with those of the previous studies by Bosse et al. (Reference Bosse, Kleiser and Meiburg2006), Monchaux & Dejoan (Reference Monchaux and Dejoan2017) and Rosa et al. (Reference Rosa, Kopeć, Ababaei and Pozorski2021).
3.6. Simulation approach and post-processing methodology
We found that very long simulation times are necessary in order to obtain converged statistics of the average vertical fluid velocity at the inertial particle position and therefore the particle settling velocity, a requirement that was also mentioned in Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Rosa et al. (Reference Rosa, Parishani, Ayala and Wang2016). As such, our statistics are computed over the very long time window of 100 large-scale eddy-turnover times. We ran the fluid only simulation for 20 ![]() $\tau _L$ and obtained the flow statistics by averaging over the last 10
$\tau _L$ and obtained the flow statistics by averaging over the last 10 ![]() $\tau _L$ (see table 1). Next, we introduced particles into the flow and ran the 1WC case for 120
$\tau _L$ (see table 1). Next, we introduced particles into the flow and ran the 1WC case for 120 ![]() $\tau _L$ and computed the 1WC statistics over the last 100
$\tau _L$ and computed the 1WC statistics over the last 100 ![]() $\tau _L$. Finally, we started the 2WC simulation from the instantaneous velocity and particle field of the completed 1WC run to obtain faster convergence of particle and fluid statistics and also because using the 1WC particle initial conditions in the 2WC regime do not affect the long-term statistics (Bosse et al. Reference Bosse, Kleiser and Meiburg2006). Similar to the 1WC case, the 2WC case was also ran for 120
$\tau _L$. Finally, we started the 2WC simulation from the instantaneous velocity and particle field of the completed 1WC run to obtain faster convergence of particle and fluid statistics and also because using the 1WC particle initial conditions in the 2WC regime do not affect the long-term statistics (Bosse et al. Reference Bosse, Kleiser and Meiburg2006). Similar to the 1WC case, the 2WC case was also ran for 120 ![]() $\tau _L$ and the 2WC statistics were computed over the last 100
$\tau _L$ and the 2WC statistics were computed over the last 100 ![]() $\tau _L$. Some of the previous works have used small averaging windows (for e.g. Good et al. Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014 and Ireland et al. Reference Ireland, Bragg and Collins2016b uses around 10
$\tau _L$. Some of the previous works have used small averaging windows (for e.g. Good et al. Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014 and Ireland et al. Reference Ireland, Bragg and Collins2016b uses around 10 ![]() $\tau _L$) and as pointed out by Rosa et al. (Reference Rosa, Parishani, Ayala and Wang2016), this could be potential reason for different quantitative results between various works. The fluid statistics can change once the two-way coupling is activated and thus the 2WC fluid statistics are only known a posteriori. As is common in 2WC studies, the particle Stokes number
$\tau _L$) and as pointed out by Rosa et al. (Reference Rosa, Parishani, Ayala and Wang2016), this could be potential reason for different quantitative results between various works. The fluid statistics can change once the two-way coupling is activated and thus the 2WC fluid statistics are only known a posteriori. As is common in 2WC studies, the particle Stokes number ![]() $St$ in the 1WC and 2WC simulations are computed based on fluid statistics of the unladen flow presented in table 1.
$St$ in the 1WC and 2WC simulations are computed based on fluid statistics of the unladen flow presented in table 1.
Table 1. Flow parameters in DNS of unladen isotropic turbulence where all dimensional parameters are in arbitrary units. ![]() $Re_{\lambda } \equiv u'\lambda /\nu = 2k/\sqrt {5/3\nu \langle \epsilon \rangle }$ is the Taylor microscale Reynolds number,
$Re_{\lambda } \equiv u'\lambda /\nu = 2k/\sqrt {5/3\nu \langle \epsilon \rangle }$ is the Taylor microscale Reynolds number, ![]() $\lambda$ is the Taylor microscale,
$\lambda$ is the Taylor microscale, ![]() $\mathcal {L}$ is the domain length,
$\mathcal {L}$ is the domain length, ![]() $N$ is the number of grid points in each direction,
$N$ is the number of grid points in each direction, ![]() $\nu$ is the fluid kinematic viscosity,
$\nu$ is the fluid kinematic viscosity, ![]() $\langle \epsilon \rangle$ is the mean turbulent kinetic energy dissipation rate,
$\langle \epsilon \rangle$ is the mean turbulent kinetic energy dissipation rate, ![]() $L$ is the integral length scale,
$L$ is the integral length scale, ![]() $\eta \equiv (\nu ^{3}/\langle \epsilon \rangle )^{1/4}$ is the Kolmogorov length scale,
$\eta \equiv (\nu ^{3}/\langle \epsilon \rangle )^{1/4}$ is the Kolmogorov length scale, ![]() $u' \equiv \sqrt {2k/3}$ is the root mean square of fluctuating fluid velocity,
$u' \equiv \sqrt {2k/3}$ is the root mean square of fluctuating fluid velocity, ![]() $k$ is the turbulent kinetic energy,
$k$ is the turbulent kinetic energy, ![]() $u_{\eta }$ is the Kolmogorov velocity scale,
$u_{\eta }$ is the Kolmogorov velocity scale, ![]() $\tau _L \equiv L/u'$ is the large-eddy-turnover time,
$\tau _L \equiv L/u'$ is the large-eddy-turnover time, ![]() $\tau _{\eta }$ is the Kolmogorov time scale,
$\tau _{\eta }$ is the Kolmogorov time scale, ![]() $k_{max} = \sqrt {2N/3}$ is the maximum resolved wavenumber,
$k_{max} = \sqrt {2N/3}$ is the maximum resolved wavenumber, ![]() $\Delta t$ is the DNS time step and
$\Delta t$ is the DNS time step and ![]() $N_{proc}$ is the number of processors used for the simulations. The small-scale resolution,
$N_{proc}$ is the number of processors used for the simulations. The small-scale resolution, ![]() $k_{max}\eta$ and the total flow kinetic energy measured by
$k_{max}\eta$ and the total flow kinetic energy measured by ![]() $u'$ are approximately constant between the different simulations. All statistics are averaged over the last 10
$u'$ are approximately constant between the different simulations. All statistics are averaged over the last 10 ![]() $\tau _L$ of the total run time of 20
$\tau _L$ of the total run time of 20 ![]() $\tau _L$ for the unladen simulations.
$\tau _L$ for the unladen simulations.

We investigate the contribution to the particle settling from different scales by computing relevant quantities filtered at various scales. We employ a sharp filter in Fourier space that filters out all the modes with wavenumber magnitude larger than the characteristic wavenumber ![]() $k_F$, which is associated with a filtering length
$k_F$, which is associated with a filtering length ![]() $\ell _F=2{\rm \pi} /k_F$ (Eyink & Aluie Reference Eyink and Aluie2009) and obtain the sub-grid field through
$\ell _F=2{\rm \pi} /k_F$ (Eyink & Aluie Reference Eyink and Aluie2009) and obtain the sub-grid field through
where ![]() $\widetilde{(\,\cdot\,)}$ denotes the coarse-grained field, while
$\widetilde{(\,\cdot\,)}$ denotes the coarse-grained field, while ![]() $(\,\cdot\,)'$ denotes the sub-grid field. We then interpolate
$(\,\cdot\,)'$ denotes the sub-grid field. We then interpolate ![]() $u'_z(\boldsymbol {x},t)$ to the positions of the inertial particles
$u'_z(\boldsymbol {x},t)$ to the positions of the inertial particles ![]() $\boldsymbol {x}^p(t)$ using an eight-point B-spline interpolation scheme to obtain
$\boldsymbol {x}^p(t)$ using an eight-point B-spline interpolation scheme to obtain ![]() ${u}'_z(\boldsymbol {x}^p(t),t)$. The values of
${u}'_z(\boldsymbol {x}^p(t),t)$. The values of ![]() ${u}'_z(\boldsymbol {x}^p(t),t)$ are then averaged over all the particles and over multiple times to obtain
${u}'_z(\boldsymbol {x}^p(t),t)$ are then averaged over all the particles and over multiple times to obtain ![]() $\langle {{u}'_z}(\boldsymbol {x}^p(t),t)\rangle$. This process is then repeated for multiple
$\langle {{u}'_z}(\boldsymbol {x}^p(t),t)\rangle$. This process is then repeated for multiple ![]() $k_F$ in order to examine the contribution of the different flow scales. This is the same approach that was adopted in our previous paper (Tom & Bragg Reference Tom and Bragg2019) for analysing the multiscale preferential sweeping mechanism.
$k_F$ in order to examine the contribution of the different flow scales. This is the same approach that was adopted in our previous paper (Tom & Bragg Reference Tom and Bragg2019) for analysing the multiscale preferential sweeping mechanism.
4. Results and discussion
4.1. Unfiltered results
We begin by considering the unfiltered results, which includes the effects of all scales in the flow on the particle settling. As discussed in § 2.1, the average particle velocity may differ from the Stokes settling velocity only if ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle \neq {0}$ and it is therefore this quantity that we focus on in order to understand how the turbulence modifies the particle settling, and how this is influenced by 2WC. We will refer to
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle \neq {0}$ and it is therefore this quantity that we focus on in order to understand how the turbulence modifies the particle settling, and how this is influenced by 2WC. We will refer to ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ as the ‘full’ settling velocity modification in subsequent discussions as it includes the effect of all the flow scales.
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ as the ‘full’ settling velocity modification in subsequent discussions as it includes the effect of all the flow scales.
In figure 1(a,b), we show the normalized settling velocity modification, ![]() $-\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle /u_\eta$, for both the 1WC and 2WC regimes for a range of
$-\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle /u_\eta$, for both the 1WC and 2WC regimes for a range of ![]() $St$ (at a fixed
$St$ (at a fixed ![]() $Re_{\lambda } = 87$) and
$Re_{\lambda } = 87$) and ![]() $Re_{\lambda }$ (at a fixed
$Re_{\lambda }$ (at a fixed ![]() $St = 1$), respectively, and for the fixed values
$St = 1$), respectively, and for the fixed values ![]() $Fr = 1$ and
$Fr = 1$ and ![]() $\varPhi _v = 1.5 \times 10^{-5}$. A positive value for
$\varPhi _v = 1.5 \times 10^{-5}$. A positive value for ![]() $-\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle = -\langle {v}_z^p(t)\rangle -St\,\tau _\eta {g}$ corresponds to turbulence-enhanced settling, whereas a negative value corresponds to turbulence-inhibited settling. The results show turbulence-enhanced settling for both 1WC and 2WC cases and that
$-\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle = -\langle {v}_z^p(t)\rangle -St\,\tau _\eta {g}$ corresponds to turbulence-enhanced settling, whereas a negative value corresponds to turbulence-inhibited settling. The results show turbulence-enhanced settling for both 1WC and 2WC cases and that ![]() $-\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle /u_\eta$ is significantly larger for the 2WC case compared with the 1WC case, as reported in previous works (Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Monchaux & Dejoan Reference Monchaux and Dejoan2017; Rosa et al. Reference Rosa, Kopeć, Ababaei and Pozorski2021). It is worth emphasizing that we see this significant enhancement even for the low volume fraction considered in this study
$-\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle /u_\eta$ is significantly larger for the 2WC case compared with the 1WC case, as reported in previous works (Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Monchaux & Dejoan Reference Monchaux and Dejoan2017; Rosa et al. Reference Rosa, Kopeć, Ababaei and Pozorski2021). It is worth emphasizing that we see this significant enhancement even for the low volume fraction considered in this study ![]() $\varPhi _v=1.5\times 10^{-5}$, where the effect of 2WC on the global flow statistics is negligible (see tables 2 and 3). This suggests, in agreement with the previous studies of Bosse et al. (Reference Bosse, Kleiser and Meiburg2006), Monchaux & Dejoan (Reference Monchaux and Dejoan2017) and Rosa et al. (Reference Rosa, Kopeć, Ababaei and Pozorski2021), that in modelling atmospheric particle transport where
$\varPhi _v=1.5\times 10^{-5}$, where the effect of 2WC on the global flow statistics is negligible (see tables 2 and 3). This suggests, in agreement with the previous studies of Bosse et al. (Reference Bosse, Kleiser and Meiburg2006), Monchaux & Dejoan (Reference Monchaux and Dejoan2017) and Rosa et al. (Reference Rosa, Kopeć, Ababaei and Pozorski2021), that in modelling atmospheric particle transport where ![]() $\varPhi _v$ is often small, the effects of 2WC on particle settling may not be negligible.
$\varPhi _v$ is often small, the effects of 2WC on particle settling may not be negligible.

Figure 1. Normalized settling velocity enhancement for the 1WC and 2WC cases at ![]() $Fr = 1$ shown as a function of (a)
$Fr = 1$ shown as a function of (a) ![]() $St$ for
$St$ for ![]() $Re_{\lambda } = 87$ and (b)
$Re_{\lambda } = 87$ and (b) ![]() $Re_{\lambda }$ for
$Re_{\lambda }$ for ![]() $St = 1$.
$St = 1$.
Table 2. Flow parameters in the DNS of particle-laden homogeneous turbulence for the 1WC and 2WC regimes in arbitrary units, and for varying Stokes number, ![]() $St$. Here,
$St$. Here, ![]() $d_p$ is the particle diameter and
$d_p$ is the particle diameter and ![]() $\Delta x$ is the grid spacing. See table 1 for the definition of other parameters. All the simulations in this table correspond to unladen simulation IV (
$\Delta x$ is the grid spacing. See table 1 for the definition of other parameters. All the simulations in this table correspond to unladen simulation IV (![]() $N =128$,
$N =128$, ![]() $Re_{\lambda } = 87$) in table 1 prior to the introduction of the particles. Note that
$Re_{\lambda } = 87$) in table 1 prior to the introduction of the particles. Note that ![]() $St$ is defined based on Kolmogorov parameters in the unladen flow. These simulations used density ratio
$St$ is defined based on Kolmogorov parameters in the unladen flow. These simulations used density ratio ![]() $\rho _p/\rho _f = 5000$, Froude number
$\rho _p/\rho _f = 5000$, Froude number ![]() $\textit {Fr} = 1$ and volume fraction
$\textit {Fr} = 1$ and volume fraction ![]() $\varPhi _v = 1.5 \times 10^{-5}$. All statistics are averaged over the last 100
$\varPhi _v = 1.5 \times 10^{-5}$. All statistics are averaged over the last 100 ![]() $\tau _L$ of the total run time of 120
$\tau _L$ of the total run time of 120 ![]() $\tau _L$ of both the 1WC and 2WC simulations.
$\tau _L$ of both the 1WC and 2WC simulations.

Table 3. Flow parameters in the DNS of particle-laden homogeneous turbulence for the 1WC and 2WC regimes in arbitrary units, and for varying Taylor Reynolds number, ![]() $Re_{\lambda }$. Here,
$Re_{\lambda }$. Here, ![]() $d_p$ is the particle diameter and
$d_p$ is the particle diameter and ![]() $\Delta x$ is the grid spacing. See table 1 for the definition of other parameters. All the simulations in this table correspond to unladen simulation with corresponding
$\Delta x$ is the grid spacing. See table 1 for the definition of other parameters. All the simulations in this table correspond to unladen simulation with corresponding ![]() $N$ in table 1 prior to the introduction of the particles. These simulations used density ratio
$N$ in table 1 prior to the introduction of the particles. These simulations used density ratio ![]() $\rho _p/\rho _f = 5000$, Froude number
$\rho _p/\rho _f = 5000$, Froude number ![]() $\textit {Fr} = 1$, Stokes number
$\textit {Fr} = 1$, Stokes number ![]() $\textit {St} = 1$ and volume fraction
$\textit {St} = 1$ and volume fraction ![]() $\varPhi _v = 1.5 \times 10^{-5}$. Note that
$\varPhi _v = 1.5 \times 10^{-5}$. Note that ![]() $St$ is defined based on Kolmogorov parameters in the unladen flow. All statistics are averaged over the last 100
$St$ is defined based on Kolmogorov parameters in the unladen flow. All statistics are averaged over the last 100 ![]() $\tau _L$ of the total run time of 120
$\tau _L$ of the total run time of 120 ![]() $\tau _L$ of both the 1WC and 2WC simulations.
$\tau _L$ of both the 1WC and 2WC simulations.
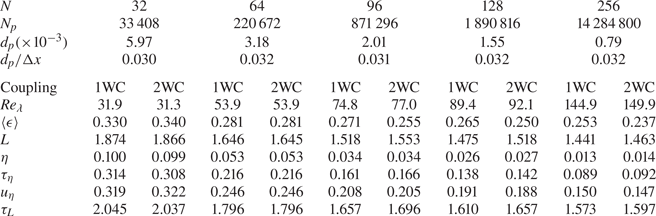
Next, we compare the quantitative values of the settling enhancement with other computational studies in table 4. The study by Rosa et al. (Reference Rosa, Kopeć, Ababaei and Pozorski2021) focuses on the microphysical processes relevant for cloud droplets in typical atmospheric flows and hence uses a density ratio ![]() $\rho _p / \rho _f = 1000$ and
$\rho _p / \rho _f = 1000$ and ![]() $Fr$ values relevant to those particular problems. Therefore, we only compare our results with the works of Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Monchaux & Dejoan (Reference Monchaux and Dejoan2017), who use the same density ratio
$Fr$ values relevant to those particular problems. Therefore, we only compare our results with the works of Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Monchaux & Dejoan (Reference Monchaux and Dejoan2017), who use the same density ratio ![]() $\rho _p / \rho _f = 5000$ and volume fraction
$\rho _p / \rho _f = 5000$ and volume fraction ![]() $\varPhi _v=1.5\times 10^{-5}$ considered in this work. While all the works referred to in table 4 show that 2WC strongly enhances the settling compared with the 1WC case, there are some differences in the values of the enhancement reported in these studies. We discuss four potential reasons for this discrepancy. First, the work by Monchaux & Dejoan (Reference Monchaux and Dejoan2017) used a particle-in-cell (PIC) method for distributing the feedback force from the particle locations to the surrounding grid points (‘feedback spreading’). While PIC is a popular method, its accuracy has been called into question because the coupling term is strongly grid dependent unless the number of particles per cell exceeds a certain threshold (Balachandar Reference Balachandar2009; Garg, Narayanan & Subramaniam Reference Garg, Narayanan and Subramaniam2009; Gualtieri et al. Reference Gualtieri, Picano, Sardina and Casciola2013, Reference Gualtieri, Picano, Sardina and Casciola2015). Second, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) used different methods for interpolation and feedback spreading and this can introduce errors into the energy balance of the system (Sundaram & Collins Reference Sundaram and Collins1996). Third, Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) made use of the ‘computational particles’ approach (Elghobashi Reference Elghobashi1994) (also referred to as the ‘super-droplet approach’), which, on the one hand, reduces the computational costs at larger mass loading, but, on the other hand, can affect the accuracy of the results. Fourth, as was demonstrated in Tom & Bragg (Reference Tom and Bragg2019), although the settling velocity enhancement depends on a restricted range (determined by
$\varPhi _v=1.5\times 10^{-5}$ considered in this work. While all the works referred to in table 4 show that 2WC strongly enhances the settling compared with the 1WC case, there are some differences in the values of the enhancement reported in these studies. We discuss four potential reasons for this discrepancy. First, the work by Monchaux & Dejoan (Reference Monchaux and Dejoan2017) used a particle-in-cell (PIC) method for distributing the feedback force from the particle locations to the surrounding grid points (‘feedback spreading’). While PIC is a popular method, its accuracy has been called into question because the coupling term is strongly grid dependent unless the number of particles per cell exceeds a certain threshold (Balachandar Reference Balachandar2009; Garg, Narayanan & Subramaniam Reference Garg, Narayanan and Subramaniam2009; Gualtieri et al. Reference Gualtieri, Picano, Sardina and Casciola2013, Reference Gualtieri, Picano, Sardina and Casciola2015). Second, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) used different methods for interpolation and feedback spreading and this can introduce errors into the energy balance of the system (Sundaram & Collins Reference Sundaram and Collins1996). Third, Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) made use of the ‘computational particles’ approach (Elghobashi Reference Elghobashi1994) (also referred to as the ‘super-droplet approach’), which, on the one hand, reduces the computational costs at larger mass loading, but, on the other hand, can affect the accuracy of the results. Fourth, as was demonstrated in Tom & Bragg (Reference Tom and Bragg2019), although the settling velocity enhancement depends on a restricted range (determined by ![]() $St$) of scales of the flow, this range could span the entire range of scales in the flows simulated in these DNS studies due to the low values of
$St$) of scales of the flow, this range could span the entire range of scales in the flows simulated in these DNS studies due to the low values of ![]() $Re_{\lambda }$. The range of velocity scales available in the flow as characterized by
$Re_{\lambda }$. The range of velocity scales available in the flow as characterized by ![]() $u'/u_{\eta }$ is different for all the three studies in table 4 and that could be another cause of the quantitative differences. However, although there are quantitative differences between our study and those of Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Monchaux & Dejoan (Reference Monchaux and Dejoan2017), we emphasize that our results are comparable to theirs, with each study demonstrating that 2WC can strongly enhance particle settling speeds in homogeneous turbulent flows. We will return later to consider the physical mechanisms responsible for 2WC leading to a strong enhancement of
$u'/u_{\eta }$ is different for all the three studies in table 4 and that could be another cause of the quantitative differences. However, although there are quantitative differences between our study and those of Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Monchaux & Dejoan (Reference Monchaux and Dejoan2017), we emphasize that our results are comparable to theirs, with each study demonstrating that 2WC can strongly enhance particle settling speeds in homogeneous turbulent flows. We will return later to consider the physical mechanisms responsible for 2WC leading to a strong enhancement of ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$.
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$.
Table 4. Comparison of settling velocity enhancement measured by ![]() $\Delta v \equiv \langle {v}_z^p(t)\rangle + \tau _p{g}$ for 1WC and 2WC flows in various studies for
$\Delta v \equiv \langle {v}_z^p(t)\rangle + \tau _p{g}$ for 1WC and 2WC flows in various studies for ![]() $\rho _p / \rho _f = 5000$ and volume fraction,
$\rho _p / \rho _f = 5000$ and volume fraction, ![]() $\varPhi _v=1.5\times 10^{-5}$. The results presented are for
$\varPhi _v=1.5\times 10^{-5}$. The results presented are for ![]() $St = 1$ and
$St = 1$ and ![]() $Sv = 1$ (and hence a
$Sv = 1$ (and hence a ![]() $Fr \equiv St / Sv = 1$). The results from Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) are based on table II (corresponding to Runs 0 and 2) and results from Monchaux & Dejoan (Reference Monchaux and Dejoan2017) are based on figure 2(a) (corresponding to Rouse number,
$Fr \equiv St / Sv = 1$). The results from Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) are based on table II (corresponding to Runs 0 and 2) and results from Monchaux & Dejoan (Reference Monchaux and Dejoan2017) are based on figure 2(a) (corresponding to Rouse number, ![]() $R \equiv v_t/u' = u_{\eta } St / u' Fr \approx 0.5$) in the corresponding manuscripts. We note that the Stokes settling velocity (
$R \equiv v_t/u' = u_{\eta } St / u' Fr \approx 0.5$) in the corresponding manuscripts. We note that the Stokes settling velocity (![]() $v_t$) for the Monchaux & Dejoan (Reference Monchaux and Dejoan2017) work is approximated as
$v_t$) for the Monchaux & Dejoan (Reference Monchaux and Dejoan2017) work is approximated as ![]() $\tau _{p}g$ instead of using the full expression
$\tau _{p}g$ instead of using the full expression ![]() $\tau _{p}g(1 - \rho _f / \rho _p)$ to obtain the above expression relating
$\tau _{p}g(1 - \rho _f / \rho _p)$ to obtain the above expression relating ![]() $R$ and
$R$ and ![]() $St$, and is justified since
$St$, and is justified since ![]() $\rho _f / \rho _p \lll 1$.
$\rho _f / \rho _p \lll 1$.
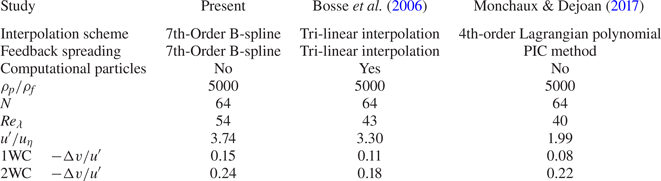
In figure 2, we present a comparison of our 1WC and 2WC DNS results for the particle settling velocity modification with selected experimental results (comparisons with these same experiments were also shown in Monchaux & Dejoan (Reference Monchaux and Dejoan2017) and Bosse et al. (Reference Bosse, Kleiser and Meiburg2006), although the latter did not compare with Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014)). Here, we provide a brief description of the experimental studies against which we compare our DNS results. Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002) studied the settling behaviour of heavy particles in homogeneous, isotropic, decaying turbulence for various particle volume fractions using a horizontal wind tunnel. Yang & Shy (Reference Yang and Shy2005) explored particle settling velocities and turbulence modification due to two-way interaction between solid particles and stationary, quasi-isotropic air turbulence using a cruciform apparatus. The particle settling velocities and root mean square velocities of water droplets in isotropic air turbulence were investigated by Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) using a ‘soccer ball’ apparatus driven by loudspeaker jets. Note that the value for ![]() $Fr$ quoted in figure 2 for the study of Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) differs from the value they report. This is because our definition of
$Fr$ quoted in figure 2 for the study of Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) differs from the value they report. This is because our definition of ![]() $Fr$ differs slightly from theirs (see § 2.1), and so we have converted the value to be consistent with our definition of
$Fr$ differs slightly from theirs (see § 2.1), and so we have converted the value to be consistent with our definition of ![]() $Fr \equiv St/Sv$.
$Fr \equiv St/Sv$.

Figure 2. Comparison of 1WC and 2WC DNS results for settling velocity modification of the current study (normalized by ![]() $u'$ and as a function of
$u'$ and as a function of ![]() $St$) with the experimental results (denoted as ‘Exp.’ in legend) of Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002) (see figure 14a), Yang & Shy (Reference Yang and Shy2005) (see figure 16a) and Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) (see figure 3a). Note that, as per our convention, vertical velocity is positive when upward and gravity is in the downward direction. Hence, positive values of
$St$) with the experimental results (denoted as ‘Exp.’ in legend) of Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002) (see figure 14a), Yang & Shy (Reference Yang and Shy2005) (see figure 16a) and Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) (see figure 3a). Note that, as per our convention, vertical velocity is positive when upward and gravity is in the downward direction. Hence, positive values of ![]() $-\langle {v}_z^p(t)\rangle -St\,\tau _\eta {g}$ imply settling enhancement and vice versa.
$-\langle {v}_z^p(t)\rangle -St\,\tau _\eta {g}$ imply settling enhancement and vice versa.
It is interesting to note that, for the ![]() $St$ range presented in figure 2, most of the experimental results show turbulence-enhanced settling, and turbulence-inhibited settling (loitering) is reported only for a limited range of the parameter space by Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014). While these experiments were chosen because they involve values of
$St$ range presented in figure 2, most of the experimental results show turbulence-enhanced settling, and turbulence-inhibited settling (loitering) is reported only for a limited range of the parameter space by Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014). While these experiments were chosen because they involve values of ![]() $Re_{\lambda }$,
$Re_{\lambda }$, ![]() $Fr$ and
$Fr$ and ![]() $\varPhi _v$ that are not too dissimilar from those of our DNS, the values of these parameters in our DNS and the experiments are different, and therefore perfect agreement is not to be expected. Nevertheless, figure 2 shows that our DNS results are within reasonable ranges compared with experimental results reported in the literature. In Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014), they attempted to perform DNS with parameters that closely matched their experiments and they found that the DNS was able to reproduce the experiments qualitatively, but there were quantitative disagreements. However, their DNS was for a 1WC system, under the assumption that this was reasonable for the dilute system they considered. In view of this, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) performed DNS of settling point particles using 2WC with parameters designed to closely match the experiments of Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002). They found that in some parameter regimes their DNS matched the experiments reasonably well, while in others the experimental results were significantly underpredicted. It is not clear, however, how much the comparison might be affected by the fact that the experiments of Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002) were for decaying turbulence, while the DNS of Monchaux & Dejoan (Reference Monchaux and Dejoan2017) was for statistically stationary turbulence (this possible impact of the turbulence decay was also discussed by Yang & Shy Reference Yang and Shy2005). Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) had also performed 2WC DNS with parameters chosen to match the experiments of Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002) and Yang & Shy (Reference Yang and Shy2005). They found that, in comparison with Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002), their simulations underpredicted the experimental values of the settling enhancement, whereas in comparison with Yang & Shy (Reference Yang and Shy2005), the DNS results for the mean particle settling velocity were considerably larger than the experimental results. Clearly then, there remains a great need for detailed quantitative tests in which DNS of point particles are designed to closely match experimental conditions in all aspects, in order to understand how well the 2WC point-particle DNS model is able to replicate the experiments. Comparisons should also be made with the more recent, detailed experiments of Petersen et al. (Reference Petersen, Baker and Coletti2019) whose experiments also explore settling in turbulent flows with higher
$\varPhi _v$ that are not too dissimilar from those of our DNS, the values of these parameters in our DNS and the experiments are different, and therefore perfect agreement is not to be expected. Nevertheless, figure 2 shows that our DNS results are within reasonable ranges compared with experimental results reported in the literature. In Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014), they attempted to perform DNS with parameters that closely matched their experiments and they found that the DNS was able to reproduce the experiments qualitatively, but there were quantitative disagreements. However, their DNS was for a 1WC system, under the assumption that this was reasonable for the dilute system they considered. In view of this, Monchaux & Dejoan (Reference Monchaux and Dejoan2017) performed DNS of settling point particles using 2WC with parameters designed to closely match the experiments of Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002). They found that in some parameter regimes their DNS matched the experiments reasonably well, while in others the experimental results were significantly underpredicted. It is not clear, however, how much the comparison might be affected by the fact that the experiments of Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002) were for decaying turbulence, while the DNS of Monchaux & Dejoan (Reference Monchaux and Dejoan2017) was for statistically stationary turbulence (this possible impact of the turbulence decay was also discussed by Yang & Shy Reference Yang and Shy2005). Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) had also performed 2WC DNS with parameters chosen to match the experiments of Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002) and Yang & Shy (Reference Yang and Shy2005). They found that, in comparison with Aliseda et al. (Reference Aliseda, Cartellier, Hainaux and Lasheras2002), their simulations underpredicted the experimental values of the settling enhancement, whereas in comparison with Yang & Shy (Reference Yang and Shy2005), the DNS results for the mean particle settling velocity were considerably larger than the experimental results. Clearly then, there remains a great need for detailed quantitative tests in which DNS of point particles are designed to closely match experimental conditions in all aspects, in order to understand how well the 2WC point-particle DNS model is able to replicate the experiments. Comparisons should also be made with the more recent, detailed experiments of Petersen et al. (Reference Petersen, Baker and Coletti2019) whose experiments also explore settling in turbulent flows with higher ![]() $Re_\lambda$. Such a detailed comparison based on our DNS code with 2WC will be presented in a future publication.
$Re_\lambda$. Such a detailed comparison based on our DNS code with 2WC will be presented in a future publication.
4.2. Contribution of different scales to the settling enhancement
Our previous study (Tom & Bragg Reference Tom and Bragg2019) highlighted the role that different flows scales have in enhancing the particle settling velocities via the multiscale preferential sweeping mechanism. We now explore how 2WC influences the role of these different scales in contributing to the particle settling velocity enhancement.
In figures 3 and 4, we consider the ratio of ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ for the 1WC and 2WC flows for varying
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ for the 1WC and 2WC flows for varying ![]() $St$ and
$St$ and ![]() $Re_{\lambda }$, respectively. Here,
$Re_{\lambda }$, respectively. Here, ![]() $u'_z$ denotes the vertical fluid velocity field with scales greater than
$u'_z$ denotes the vertical fluid velocity field with scales greater than ![]() $\ell _F$ filtered out (i.e. it is the ‘sub-grid field’), such that
$\ell _F$ filtered out (i.e. it is the ‘sub-grid field’), such that ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ denotes the contribution of all scales less than or equal to
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ denotes the contribution of all scales less than or equal to ![]() $\ell _F$ to the full quantity
$\ell _F$ to the full quantity ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$. The results show a very strong modification of
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$. The results show a very strong modification of ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ due to 2WC at the small scales. Indeed, the insets in figures 3 and 4 show that 2WC enhances
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ due to 2WC at the small scales. Indeed, the insets in figures 3 and 4 show that 2WC enhances ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ at small scales by 2 to 3 orders of magnitude. It can also be seen that the impact of 2WC on
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ at small scales by 2 to 3 orders of magnitude. It can also be seen that the impact of 2WC on ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ reduces as
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ reduces as ![]() $\ell _F$ is increased. This can be explained using the idea of a filter scale-dependent Stokes number,
$\ell _F$ is increased. This can be explained using the idea of a filter scale-dependent Stokes number, ![]() $St_{\ell }\equiv \tau _p/\tau _{\ell }$ introduced in § 2.2, which quantifies the importance of particle inertia with respect to its impact on how the particle interacts with turbulent eddies of size
$St_{\ell }\equiv \tau _p/\tau _{\ell }$ introduced in § 2.2, which quantifies the importance of particle inertia with respect to its impact on how the particle interacts with turbulent eddies of size ![]() $\ell$. Since
$\ell$. Since ![]() $\tau _{\ell }$ is a non-decreasing function of
$\tau _{\ell }$ is a non-decreasing function of ![]() $\ell$ in homogeneous turbulence, then
$\ell$ in homogeneous turbulence, then ![]() $St_\ell$ is correspondingly a non-increasing function of
$St_\ell$ is correspondingly a non-increasing function of ![]() $\ell$. For point particles, it is ultimately the inertia of the particles that enables them to modify the flow via 2WC, and so
$\ell$. For point particles, it is ultimately the inertia of the particles that enables them to modify the flow via 2WC, and so ![]() $St_\ell$ should determine whether 2WC is important at a given scale. In our DNS, since we consider
$St_\ell$ should determine whether 2WC is important at a given scale. In our DNS, since we consider ![]() $St\leq O(1)$, then as the filter scale
$St\leq O(1)$, then as the filter scale ![]() $\ell =\ell _F$ is increased,
$\ell =\ell _F$ is increased, ![]() $St_\ell$ monotonically decreases from
$St_\ell$ monotonically decreases from ![]() $O(1)$ to smaller values, implying that the effect of 2WC should also monotonically decrease with increasing
$O(1)$ to smaller values, implying that the effect of 2WC should also monotonically decrease with increasing ![]() $\ell$. This is essentially what is observed in figures 3 and 4. Some of the curves in these plots do, however, approach an approximately constant value (the value depending on
$\ell$. This is essentially what is observed in figures 3 and 4. Some of the curves in these plots do, however, approach an approximately constant value (the value depending on ![]() $St$ and
$St$ and ![]() $Re_\lambda$) as
$Re_\lambda$) as ![]() $\ell _F$ approaches/exceeds the largest values. For the
$\ell _F$ approaches/exceeds the largest values. For the ![]() $Re_\lambda$ of our DNS, this is mainly due to the fact that the largest
$Re_\lambda$ of our DNS, this is mainly due to the fact that the largest ![]() $\ell _F$ are of the order of the integral length scale of the flow
$\ell _F$ are of the order of the integral length scale of the flow ![]() $L$, and the curves must be constant for
$L$, and the curves must be constant for ![]() $\ell _F> O(L)$ (the case with
$\ell _F> O(L)$ (the case with ![]() $Re_{\lambda } = 142$ in figure 4 clearly satisfies this limiting behaviour, for which
$Re_{\lambda } = 142$ in figure 4 clearly satisfies this limiting behaviour, for which ![]() $L/\eta \approx 105$). However, in a flow with
$L/\eta \approx 105$). However, in a flow with ![]() $Re_\lambda \to \infty$,
$Re_\lambda \to \infty$, ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ would be constant
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ would be constant ![]() $\forall \ell _F>\ell _c(St)$ for both the 1WC and 2WC flows, and therefore their ratio would also approach a constant. This is because scales larger than
$\forall \ell _F>\ell _c(St)$ for both the 1WC and 2WC flows, and therefore their ratio would also approach a constant. This is because scales larger than ![]() $\ell _c$ do not contribute to the settling velocity of the particles since particle inertia is negligible at these scales, and also therefore is the effect of 2WC.
$\ell _c$ do not contribute to the settling velocity of the particles since particle inertia is negligible at these scales, and also therefore is the effect of 2WC.
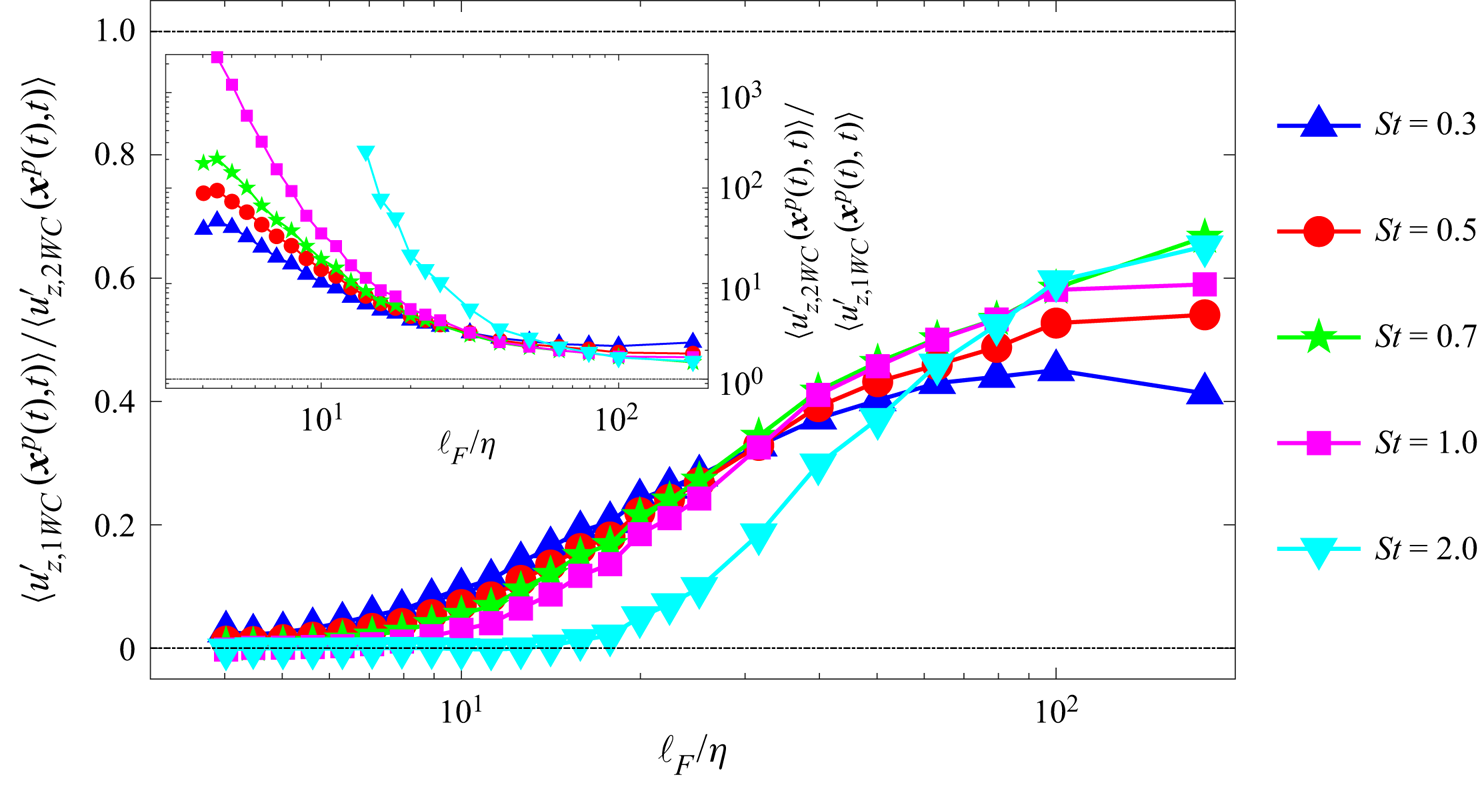
Figure 3. Ratio of 1WC sub-grid settling velocity enhancement to that of the 2WC case shown as a function of the normalized filtering length ![]() $\ell _F/\eta$ for varying
$\ell _F/\eta$ for varying ![]() $St$ and fixed
$St$ and fixed ![]() $Re_{\lambda } = 87$ and
$Re_{\lambda } = 87$ and ![]() $Fr = 1$. Inset shows the ratio of 2WC to 1WC case and helps to infer magnitude of enhancement by 2WC. Inset is in log–log scale and some values at low
$Fr = 1$. Inset shows the ratio of 2WC to 1WC case and helps to infer magnitude of enhancement by 2WC. Inset is in log–log scale and some values at low ![]() $\ell _F / \eta$ are not shown here because of ‘noise’ in the data.
$\ell _F / \eta$ are not shown here because of ‘noise’ in the data.

Figure 4. Ratio of 1WC sub-grid settling velocity enhancement to that of the 2WC case shown as a function of the normalized filtering length ![]() $\ell _F/\eta$ for varying
$\ell _F/\eta$ for varying ![]() $Re_{\lambda }$ and fixed
$Re_{\lambda }$ and fixed ![]() $St = 1$ and
$St = 1$ and ![]() $Fr = 1$. Inset shows the ratio of 2WC to 1WC case and helps to infer magnitude of enhancement by 2WC. Inset is in log–log scale and some values at low
$Fr = 1$. Inset shows the ratio of 2WC to 1WC case and helps to infer magnitude of enhancement by 2WC. Inset is in log–log scale and some values at low ![]() $\ell _F / \eta$ are not shown here because of ‘noise’ in the data.
$\ell _F / \eta$ are not shown here because of ‘noise’ in the data.
In figure 3, we see that for low values of ![]() $\ell _F$, say
$\ell _F$, say ![]() $\ell _F/\eta < 20$, the effect of 2WC is larger for higher
$\ell _F/\eta < 20$, the effect of 2WC is larger for higher ![]() $St$. However, we see an opposite trend for larger
$St$. However, we see an opposite trend for larger ![]() $\ell _F/\eta$. This trend reversal at smaller and larger scales is analogous to the ‘pivoting’ of energy spectrum observed in 2WC flows and a more detailed future investigation is required to understand this phenomenon. The results also show that
$\ell _F/\eta$. This trend reversal at smaller and larger scales is analogous to the ‘pivoting’ of energy spectrum observed in 2WC flows and a more detailed future investigation is required to understand this phenomenon. The results also show that ![]() $|\langle u'_z(\boldsymbol {x}^p(t),t)\rangle |$ is greater for the 2WC than the 1WC case at all scales considered. However, this need not imply that 2WC is important at all the scales of the flow considered, since
$|\langle u'_z(\boldsymbol {x}^p(t),t)\rangle |$ is greater for the 2WC than the 1WC case at all scales considered. However, this need not imply that 2WC is important at all the scales of the flow considered, since ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ involves contributions from all scales less than
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ involves contributions from all scales less than ![]() $\ell _F$, and therefore should not be interpreted as being determined by the particular scale,
$\ell _F$, and therefore should not be interpreted as being determined by the particular scale, ![]() $\ell _F$. To isolate the effect of 2WC on any particular scale, one would have to employ a method that is local in scale space (e.g. Fourier analysis), or else to consider
$\ell _F$. To isolate the effect of 2WC on any particular scale, one would have to employ a method that is local in scale space (e.g. Fourier analysis), or else to consider ![]() $\langle {u''}_z(\boldsymbol {x}^p(t),t)\rangle$, where
$\langle {u''}_z(\boldsymbol {x}^p(t),t)\rangle$, where ![]() $u''$ corresponds to the velocity field formed by filtering out (removing) scales less than
$u''$ corresponds to the velocity field formed by filtering out (removing) scales less than ![]() $(1-\alpha ) \ell _F$ and greater than
$(1-\alpha ) \ell _F$ and greater than ![]() $(1+\alpha ) \ell _F$, where
$(1+\alpha ) \ell _F$, where ![]() $0<\alpha \ll 1$.
$0<\alpha \ll 1$.
As highlighted earlier, although the effect of 2WC on ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ is very strong at the smallest scales, its effect on the full quantity
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ is very strong at the smallest scales, its effect on the full quantity ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ is less dramatic. To understand why this is so we look at the contribution of different scales to the full quantity
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ is less dramatic. To understand why this is so we look at the contribution of different scales to the full quantity ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ in figures 5 and 6. We see that the smallest scales where the effect of 2WC is most significant, i.e.
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ in figures 5 and 6. We see that the smallest scales where the effect of 2WC is most significant, i.e. ![]() $\ell _F / \eta \lesssim 20$, only contribute approximately
$\ell _F / \eta \lesssim 20$, only contribute approximately ![]() $10\unicode{x2013}20\,\%$ of the full quantity
$10\unicode{x2013}20\,\%$ of the full quantity ![]() $\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$. Note that in these results,
$\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$. Note that in these results, ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle /\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ does not saturate with increasing
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle /\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ does not saturate with increasing ![]() $\ell _F/\eta$, but only reaches a value of unity when all scales of the flow are included. According to the theory in Tom & Bragg (Reference Tom and Bragg2019), for
$\ell _F/\eta$, but only reaches a value of unity when all scales of the flow are included. According to the theory in Tom & Bragg (Reference Tom and Bragg2019), for ![]() $Re_\lambda \to \infty$ the quantity
$Re_\lambda \to \infty$ the quantity ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle /\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ would approach unity in the limit
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle /\langle {u}_z(\boldsymbol {x}^p(t),t)\rangle$ would approach unity in the limit ![]() $\ell _F\to \ell _c(St)\ll L$ (assuming
$\ell _F\to \ell _c(St)\ll L$ (assuming ![]() $St$ is finite), where
$St$ is finite), where ![]() $\ell _c(St)$ is defined as the scale above which the effects of particle inertia are negligible. Since 2WC arises due to the particles not following the local fluid velocity field due to their inertia, then
$\ell _c(St)$ is defined as the scale above which the effects of particle inertia are negligible. Since 2WC arises due to the particles not following the local fluid velocity field due to their inertia, then ![]() $\ell _c(St)$ must also provide an upper bound on the scale at which 2WC can impact the flow. The
$\ell _c(St)$ must also provide an upper bound on the scale at which 2WC can impact the flow. The ![]() $Re_\lambda$ of our DNS are too small to observe these asymptotic regimes which are, however, likely be of importance in atmospheric contexts where typically
$Re_\lambda$ of our DNS are too small to observe these asymptotic regimes which are, however, likely be of importance in atmospheric contexts where typically ![]() $Re_\lambda \geq (10^4)$.
$Re_\lambda \geq (10^4)$.

Figure 5. Ratio of sub-grid settling velocity enhancement to the ‘full’ settling velocity enhancement for the 1WC (open symbols, dashed line) and 2WC (closed symbols, solid line) cases shown as a function of the normalized filtering length ![]() $\ell _F/\eta$ for varying
$\ell _F/\eta$ for varying ![]() $St$ and fixed
$St$ and fixed ![]() $Re_{\lambda } = 87$ and
$Re_{\lambda } = 87$ and ![]() $Fr = 1$.
$Fr = 1$.

Figure 6. Ratio of sub-grid settling velocity enhancement to the ‘full’ settling velocity enhancement for the 1WC (open symbols, dashed line) and 2WC (closed symbols, solid line) cases shown as a function of the normalized filtering length ![]() $\ell _F/\eta$ for varying
$\ell _F/\eta$ for varying ![]() $Re_{\lambda }$ and fixed
$Re_{\lambda }$ and fixed ![]() $St = 1$ and
$St = 1$ and ![]() $Fr = 1$.
$Fr = 1$.
4.3. Effectiveness of the preferential sweeping mechanism in 2WC flows
Having explored the role of different flow scales that contribute to ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$, we now turn to consider the role played by the preferential sweeping mechanism in governing
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$, we now turn to consider the role played by the preferential sweeping mechanism in governing ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$, and to understand how 2WC leads to the strong enhancement of this quantity that was observed earlier. This is especially important to consider since Monchaux & Dejoan (Reference Monchaux and Dejoan2017) argued that in the presence of 2WC, the role of preferential sweeping is reduced, and possibly even eradicated, and that instead
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$, and to understand how 2WC leads to the strong enhancement of this quantity that was observed earlier. This is especially important to consider since Monchaux & Dejoan (Reference Monchaux and Dejoan2017) argued that in the presence of 2WC, the role of preferential sweeping is reduced, and possibly even eradicated, and that instead ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle <0$ is mainly due to the particles dragging the surrounding fluid down with them as they fall.
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle <0$ is mainly due to the particles dragging the surrounding fluid down with them as they fall.
Many previous studies have sought to detect the role of preferential sweeping by considering the fluid statistics conditioned on the local particle concentration. However, as discussed in Tom & Bragg (Reference Tom and Bragg2019), this is inappropriate for investigating the role of the preferential sweeping mechanism. Instead, one needs to consider the local fluid velocity conditioned on the local flow structure (since the preferential sweeping mechanism specifically argues that the settling enhancement is due to the particle motion in strain-dominated regions of the flow), and to consider this we introduce the invariant
with which we may write
where ![]() $\mathcal {P}({\mathcal {Q}},t)\equiv \langle \delta ({\mathcal {Q}}^p(t)-{\mathcal {Q}})\rangle$ is the PDF of
$\mathcal {P}({\mathcal {Q}},t)\equiv \langle \delta ({\mathcal {Q}}^p(t)-{\mathcal {Q}})\rangle$ is the PDF of ![]() ${\mathcal {Q}}^p(t)$, and
${\mathcal {Q}}^p(t)$, and ![]() $\mathcal {Q}$ is the corresponding sample-space coordinate. Here,
$\mathcal {Q}$ is the corresponding sample-space coordinate. Here, ![]() $\mathcal {S}^2$ and
$\mathcal {S}^2$ and ![]() $\mathcal {R}^2$ are the second invariants of the strain rate
$\mathcal {R}^2$ are the second invariants of the strain rate ![]() $\boldsymbol {\mathcal {S}}\equiv (\boldsymbol {\nabla u}+\boldsymbol {\nabla u}^\top )/2$ and rotation rate
$\boldsymbol {\mathcal {S}}\equiv (\boldsymbol {\nabla u}+\boldsymbol {\nabla u}^\top )/2$ and rotation rate ![]() $\boldsymbol {\mathcal {R}}\equiv (\boldsymbol {\nabla u}-\boldsymbol {\nabla u}^\top )/2$ tensors, respectively.
$\boldsymbol {\mathcal {R}}\equiv (\boldsymbol {\nabla u}-\boldsymbol {\nabla u}^\top )/2$ tensors, respectively.
We may then define
According to the preferential sweeping mechanism, we would expect ![]() $|B(0)|>|A(0)|$ with
$|B(0)|>|A(0)|$ with ![]() $B(0)<0$, i.e.
$B(0)<0$, i.e. ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is dominated by contributions from particles in strain-dominated regions of the flow (where
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is dominated by contributions from particles in strain-dominated regions of the flow (where ![]() ${\mathcal {Q}}>0$), and in these regions the particles experience on average a downward moving fluid velocity.
${\mathcal {Q}}>0$), and in these regions the particles experience on average a downward moving fluid velocity.
The results in figure 7 clearly show that ![]() $|B(0)|>|A(0)|$ and
$|B(0)|>|A(0)|$ and ![]() $B(0)<0$ for both the 1WC and 2WC cases, confirming the role of the preferential sweeping mechanism in both cases. It is interesting to note that, even for the 1WC case,
$B(0)<0$ for both the 1WC and 2WC cases, confirming the role of the preferential sweeping mechanism in both cases. It is interesting to note that, even for the 1WC case, ![]() $A(0)$ is also negative, implying that even when the particles are in a rotation-dominated region, they still experience an enhanced settling due to the turbulence. While this may seem surprising, it is not inconsistent with the preferential sweeping mechanism for at least two reasons. First, the preferential sweeping mechanism simply argues that the dominant contribution to
$A(0)$ is also negative, implying that even when the particles are in a rotation-dominated region, they still experience an enhanced settling due to the turbulence. While this may seem surprising, it is not inconsistent with the preferential sweeping mechanism for at least two reasons. First, the preferential sweeping mechanism simply argues that the dominant contribution to ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is from particles that move in strain-dominated regions, and does not say anything explicitly about what the contribution to
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is from particles that move in strain-dominated regions, and does not say anything explicitly about what the contribution to ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is from the sub-set of particles that move through rotation-dominated regions of the flow. Second, if the inertial particle falls through a vortex (where
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is from the sub-set of particles that move through rotation-dominated regions of the flow. Second, if the inertial particle falls through a vortex (where ![]() $\mathcal {Q}<0$), then provided it still has the tendency to fall through the downward side of the vortex, then in this region the particle would also experience a downward moving flow, enabling one to have
$\mathcal {Q}<0$), then provided it still has the tendency to fall through the downward side of the vortex, then in this region the particle would also experience a downward moving flow, enabling one to have ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle _{\mathcal {Q}<0}<0$.
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle _{\mathcal {Q}<0}<0$.

Figure 7. DNS results for ![]() $A(0)/u_\eta$ and
$A(0)/u_\eta$ and ![]() $B(0)/u_\eta$ as a function of
$B(0)/u_\eta$ as a function of ![]() $St$ and for the 1WC and 2WC cases. Here,
$St$ and for the 1WC and 2WC cases. Here, ![]() $A(0)$ denotes the total contribution to
$A(0)$ denotes the total contribution to ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ from particles in rotation-dominated regions of the flow, while
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ from particles in rotation-dominated regions of the flow, while ![]() $B(0)$ denotes the total contribution to
$B(0)$ denotes the total contribution to ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ from particles in strain-dominated regions of the flow.
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ from particles in strain-dominated regions of the flow.
The results in figure 7 show that 2WC enhances both ![]() $|A(0)|$ and
$|A(0)|$ and ![]() $|B(0)|$, and this is plausibly explained in terms of the fluid dragging effect discussed in Monchaux & Dejoan (Reference Monchaux and Dejoan2017). Namely, as the particles fall through the flow, they tend to accelerate the fluid downward on average, which then enhances the downward velocity of the fluid in the vicinity of the particles. Nevertheless, the results in figure 7 imply that this dragging effect occurs in both strain- and rotation-dominated regions of the flow, and that overall the turbulence enhancement of the particle settling velocity continues to be dominated by contributions from particles in strain-dominated regions of the flow. Put together, this means that
$|B(0)|$, and this is plausibly explained in terms of the fluid dragging effect discussed in Monchaux & Dejoan (Reference Monchaux and Dejoan2017). Namely, as the particles fall through the flow, they tend to accelerate the fluid downward on average, which then enhances the downward velocity of the fluid in the vicinity of the particles. Nevertheless, the results in figure 7 imply that this dragging effect occurs in both strain- and rotation-dominated regions of the flow, and that overall the turbulence enhancement of the particle settling velocity continues to be dominated by contributions from particles in strain-dominated regions of the flow. Put together, this means that ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is dominated by contributions from particles in strain-dominated regions of the flow, and that for the 2WC case, in these regions the particles also drag the fluid with them, increasing the local fluid velocity and hence enhancing
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is dominated by contributions from particles in strain-dominated regions of the flow, and that for the 2WC case, in these regions the particles also drag the fluid with them, increasing the local fluid velocity and hence enhancing ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ compared with the 1WC case. These results then provide strong evidence that the preferential sweeping mechanism continues to be the basic mechanism by which the turbulence enhances the particle settling velocity compared with the Stokes settling velocity.
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ compared with the 1WC case. These results then provide strong evidence that the preferential sweeping mechanism continues to be the basic mechanism by which the turbulence enhances the particle settling velocity compared with the Stokes settling velocity.
In figure 8, we show the ratios ![]() $B(\alpha _1)/A(\alpha _1)$ and
$B(\alpha _1)/A(\alpha _1)$ and ![]() $B(\alpha _2)/A(\alpha _2)$ with
$B(\alpha _2)/A(\alpha _2)$ with ![]() $\alpha _1=0$ and
$\alpha _1=0$ and ![]() $\alpha _2=4\langle \mathcal {S}^2\rangle$. The results show that
$\alpha _2=4\langle \mathcal {S}^2\rangle$. The results show that ![]() $B(\alpha _1)/A(\alpha _1)$ is greater than 1 and that 2WC has a relatively small effect on this ratio. On the other hand, the results for
$B(\alpha _1)/A(\alpha _1)$ is greater than 1 and that 2WC has a relatively small effect on this ratio. On the other hand, the results for ![]() $B(\alpha _2)/A(\alpha _2)$ are much larger and show a much stronger effect of 2WC. These results with
$B(\alpha _2)/A(\alpha _2)$ are much larger and show a much stronger effect of 2WC. These results with ![]() $\alpha _2=4\langle \mathcal {S}^2\rangle$ only consider contributions from regions of strong strain (
$\alpha _2=4\langle \mathcal {S}^2\rangle$ only consider contributions from regions of strong strain (![]() $\mathcal {Q}>4\langle \mathcal {S}^2\rangle$) and strong rotation (
$\mathcal {Q}>4\langle \mathcal {S}^2\rangle$) and strong rotation (![]() $\mathcal {Q}<-4\langle \mathcal {S}^2\rangle$), and isolating these regions reveals a very strong effect of preferential sweeping. This is most likely due to the fact that
$\mathcal {Q}<-4\langle \mathcal {S}^2\rangle$), and isolating these regions reveals a very strong effect of preferential sweeping. This is most likely due to the fact that ![]() $A$ and
$A$ and ![]() $B$ for
$B$ for ![]() $\alpha =0$ are dominated by contributions to their integrals from regions where
$\alpha =0$ are dominated by contributions to their integrals from regions where ![]() $\mathcal {Q}$ is not that large, e.g.
$\mathcal {Q}$ is not that large, e.g. ![]() $|\mathcal {Q}|\leq O(\langle \mathcal {S}^2\rangle )$, and in such a region,
$|\mathcal {Q}|\leq O(\langle \mathcal {S}^2\rangle )$, and in such a region, ![]() $\mathcal {Q}<0$ might be associated with rotational fluid motion that is also accompanied by significant straining, i.e. not regions of solid-body rotation. On the other hand, regions where
$\mathcal {Q}<0$ might be associated with rotational fluid motion that is also accompanied by significant straining, i.e. not regions of solid-body rotation. On the other hand, regions where ![]() $\mathcal {Q}\ll -\langle \mathcal {S}^2\rangle$ are more likely to be associated with regions of quasi-solid-body rotation, and it is these regions that are most effective in centrifuging the inertial particles.
$\mathcal {Q}\ll -\langle \mathcal {S}^2\rangle$ are more likely to be associated with regions of quasi-solid-body rotation, and it is these regions that are most effective in centrifuging the inertial particles.

Figure 8. DNS results for ![]() $B(\alpha )/A(\alpha )$ as a function of
$B(\alpha )/A(\alpha )$ as a function of ![]() $St$ and for the 1WC and 2WC cases. In the plots,
$St$ and for the 1WC and 2WC cases. In the plots, ![]() $\alpha _1=0$ and
$\alpha _1=0$ and ![]() $\alpha _2=4\langle \mathcal {S}^2\rangle$. Here,
$\alpha _2=4\langle \mathcal {S}^2\rangle$. Here, ![]() $A(\alpha )$ denotes the total contribution to
$A(\alpha )$ denotes the total contribution to ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ from particles in regions of the flow where
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ from particles in regions of the flow where ![]() $\mathcal {Q}<-\alpha$, while
$\mathcal {Q}<-\alpha$, while ![]() $B(\alpha )$ denotes the total contribution to
$B(\alpha )$ denotes the total contribution to ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ from particles in regions of the flow where
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ from particles in regions of the flow where ![]() $\mathcal {Q}>\alpha$.
$\mathcal {Q}>\alpha$.
Since ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ is an odd moment that depends delicately on how the settling particles sample the flow, another way to substantiate the idea that 2WC enhances the particle settling compared with the 1WC due to the fluid dragging effect is to also consider the influence of 2WC on the second moment
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ is an odd moment that depends delicately on how the settling particles sample the flow, another way to substantiate the idea that 2WC enhances the particle settling compared with the 1WC due to the fluid dragging effect is to also consider the influence of 2WC on the second moment ![]() $\langle u'^{2}_z(\boldsymbol {x}^p(t),t)\rangle$ which would be finite even for non-settling, non-inertial particles. In figures 9 and 10, we show the ratio of
$\langle u'^{2}_z(\boldsymbol {x}^p(t),t)\rangle$ which would be finite even for non-settling, non-inertial particles. In figures 9 and 10, we show the ratio of ![]() $\langle u'^{2}_z(\boldsymbol {x}^p(t),t)\rangle$ for the 1WC to the 2WC case. It can be clearly seen that the fluid velocity fluctuations sampled by the particle are larger in the 2WC case, which is again plausibly due to the fluid dragging effect discussed in Monchaux & Dejoan (Reference Monchaux and Dejoan2017). Comparing the results in figures 9 and 10 to those in figures 3 and 4 shows that the first moment of
$\langle u'^{2}_z(\boldsymbol {x}^p(t),t)\rangle$ for the 1WC to the 2WC case. It can be clearly seen that the fluid velocity fluctuations sampled by the particle are larger in the 2WC case, which is again plausibly due to the fluid dragging effect discussed in Monchaux & Dejoan (Reference Monchaux and Dejoan2017). Comparing the results in figures 9 and 10 to those in figures 3 and 4 shows that the first moment of ![]() $u'_z(\boldsymbol {x}^p(t),t)$ is more sensitive to 2WC than the second moments. This is likely due to the more general fact that odd moments of flow quantities evaluated along particle trajectories are often much more sensitive to the effects of particle inertia (and therefore 2WC) than even moments since odd moments depend sensitively on cancellation between positive and negative values of the random variable (e.g. see figure 6 in Bragg Reference Bragg2017).
$u'_z(\boldsymbol {x}^p(t),t)$ is more sensitive to 2WC than the second moments. This is likely due to the more general fact that odd moments of flow quantities evaluated along particle trajectories are often much more sensitive to the effects of particle inertia (and therefore 2WC) than even moments since odd moments depend sensitively on cancellation between positive and negative values of the random variable (e.g. see figure 6 in Bragg Reference Bragg2017).

Figure 9. Ratio of variances of 1WC sub-grid settling velocity enhancement to that of the 2WC case shown as a function of the normalized filtering length ![]() $\ell _F/\eta$ for varying
$\ell _F/\eta$ for varying ![]() $St$ and fixed
$St$ and fixed ![]() $Re_{\lambda } = 87$ and
$Re_{\lambda } = 87$ and ![]() $Fr = 1$.
$Fr = 1$.

Figure 10. Ratio of variances of 1WC sub-grid settling velocity enhancement to that of the 2WC case shown as a function of the normalized filtering length ![]() $\ell _F/\eta$ for varying
$\ell _F/\eta$ for varying ![]() $Re_{\lambda }$ and fixed
$Re_{\lambda }$ and fixed ![]() $St = 1$ and
$St = 1$ and ![]() $Fr = 1$.
$Fr = 1$.
In contrast to Monchaux & Dejoan (Reference Monchaux and Dejoan2017) therefore, these results provide strong evidence that, at least for the ![]() $\varPhi _m$ considered, preferential sweeping continues to be the mechanism responsible for the enhanced particle settling, with the contribution of 2WC being mainly that in the downward, strain-dominated regions where the particles preferentially move due to the centrifuging effect, the particles drag the fluid down with them, further enhancing their settling compared with that produced by preferential sweeping in the 1WC case. The result that led Monchaux & Dejoan (Reference Monchaux and Dejoan2017) to conclude that 2WC strongly reduces the role of preferential sweeping was based on their observation that if they compute the PDF of the fluid velocity gradients along the settling inertial particle trajectories, then as either
$\varPhi _m$ considered, preferential sweeping continues to be the mechanism responsible for the enhanced particle settling, with the contribution of 2WC being mainly that in the downward, strain-dominated regions where the particles preferentially move due to the centrifuging effect, the particles drag the fluid down with them, further enhancing their settling compared with that produced by preferential sweeping in the 1WC case. The result that led Monchaux & Dejoan (Reference Monchaux and Dejoan2017) to conclude that 2WC strongly reduces the role of preferential sweeping was based on their observation that if they compute the PDF of the fluid velocity gradients along the settling inertial particle trajectories, then as either ![]() $Sv$ or
$Sv$ or ![]() $\varPhi _m$ is increased, the preferential sampling of the flow (on which the preferential sweeping mechanism depends) is dramatically reduced. However, contrary to their interpretation, this does not necessarily mean that the preferential sweeping mechanism is ceasing to play a role in governing the particle settling. Indeed, as was explained and demonstrated in Tom & Bragg (Reference Tom and Bragg2019), even for a 1WC system, as
$\varPhi _m$ is increased, the preferential sampling of the flow (on which the preferential sweeping mechanism depends) is dramatically reduced. However, contrary to their interpretation, this does not necessarily mean that the preferential sweeping mechanism is ceasing to play a role in governing the particle settling. Indeed, as was explained and demonstrated in Tom & Bragg (Reference Tom and Bragg2019), even for a 1WC system, as ![]() $Sv$ is increased, the scales of the flow at which the preferential sweeping mechanism operates shifts to larger scales. Here, we provide a brief summary of our argument for this, and refer the reader to Tom & Bragg (Reference Tom and Bragg2019) for more details (specifically, §§ 2.4.3 and 4.3 and the discussion surrounding the 1WC DNS results in figures 10 and 11).
$Sv$ is increased, the scales of the flow at which the preferential sweeping mechanism operates shifts to larger scales. Here, we provide a brief summary of our argument for this, and refer the reader to Tom & Bragg (Reference Tom and Bragg2019) for more details (specifically, §§ 2.4.3 and 4.3 and the discussion surrounding the 1WC DNS results in figures 10 and 11).
Usually, preferential sampling of the flow is said to be strongest at scales where ![]() $St_\ell =O(1)$. However, to be more precise in the presence of gravity, the relevant parameter quantifying the effect of particle inertia with respect to a particular flow scale (
$St_\ell =O(1)$. However, to be more precise in the presence of gravity, the relevant parameter quantifying the effect of particle inertia with respect to a particular flow scale (![]() $\ell$) is the eddy-turnover time scale seen by the particle (
$\ell$) is the eddy-turnover time scale seen by the particle (![]() $T_\ell$) instead of the eddy-turnover time scale at that scale (
$T_\ell$) instead of the eddy-turnover time scale at that scale (![]() $\tau _\ell$). Hence, in the presence of gravity, we need to use a revised definition of the scale-dependent Stokes number,
$\tau _\ell$). Hence, in the presence of gravity, we need to use a revised definition of the scale-dependent Stokes number, ![]() $St_{\ell }^* \equiv \tau _p / T_\ell$, instead of
$St_{\ell }^* \equiv \tau _p / T_\ell$, instead of ![]() $St_{\ell }\equiv \tau _p/\tau _{\ell }$ normally employed. In cases with gravity, the preferential concentration is strongest at scales where
$St_{\ell }\equiv \tau _p/\tau _{\ell }$ normally employed. In cases with gravity, the preferential concentration is strongest at scales where ![]() $St_\ell ^*=O(1)$. The time scale
$St_\ell ^*=O(1)$. The time scale ![]() $T_\ell$ depends upon
$T_\ell$ depends upon ![]() $St$ and
$St$ and ![]() $Fr$ and like
$Fr$ and like ![]() $\tau _\ell$, is a non-decreasing function of
$\tau _\ell$, is a non-decreasing function of ![]() $\ell$. For a given
$\ell$. For a given ![]() $\tau _p$ and
$\tau _p$ and ![]() $\ell$,
$\ell$, ![]() $T_\ell$ decreases as
$T_\ell$ decreases as ![]() $Fr$ is reduced since the fluid velocity along its trajectory will decorrelate faster, the so-called ‘crossing trajectories effect’ (Csanady Reference Csanady1973). Hence, for a given
$Fr$ is reduced since the fluid velocity along its trajectory will decorrelate faster, the so-called ‘crossing trajectories effect’ (Csanady Reference Csanady1973). Hence, for a given ![]() $St$, as
$St$, as ![]() $Fr$ is reduced,
$Fr$ is reduced, ![]() $St_{\ell }^*=O(1)$ is satisfied at increasingly larger scales. Since the preferential sampling will be strongest at scales where
$St_{\ell }^*=O(1)$ is satisfied at increasingly larger scales. Since the preferential sampling will be strongest at scales where ![]() $St_\ell ^*=O(1)$, this then means that as the particles fall faster through the flow, the scales at which the preferential sampling is strongest shifts to larger and larger scales. As such, for sufficiently large
$St_\ell ^*=O(1)$, this then means that as the particles fall faster through the flow, the scales at which the preferential sampling is strongest shifts to larger and larger scales. As such, for sufficiently large ![]() $Sv$, one will not observe preferential sampling of the unfiltered velocity gradients (as was observed in Monchaux & Dejoan Reference Monchaux and Dejoan2017) because at those scales in the dissipation range we might have
$Sv$, one will not observe preferential sampling of the unfiltered velocity gradients (as was observed in Monchaux & Dejoan Reference Monchaux and Dejoan2017) because at those scales in the dissipation range we might have ![]() $St_\ell ^*\gg O(1)$. We may nevertheless observe preferential sampling of the velocity gradients filtered at a scale
$St_\ell ^*\gg O(1)$. We may nevertheless observe preferential sampling of the velocity gradients filtered at a scale ![]() $\ell$ for which
$\ell$ for which ![]() $St_\ell ^*=O(1)$.
$St_\ell ^*=O(1)$.
As an aside, the effect just discussed also explains why in figure 2 the curves based on the data from Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) move to the left (smaller ![]() $St$) as
$St$) as ![]() $Fr$ is decreased. In particular, as
$Fr$ is decreased. In particular, as ![]() $Fr$ is decreased,
$Fr$ is decreased, ![]() $T_{\ell =\eta }$ decreases, and hence the value of
$T_{\ell =\eta }$ decreases, and hence the value of ![]() $\tau _p$ for which
$\tau _p$ for which ![]() $St^*_{\ell =\eta }=O(1)$ corresponds to a smaller value of
$St^*_{\ell =\eta }=O(1)$ corresponds to a smaller value of ![]() $\tau _p$ (and therefore smaller
$\tau _p$ (and therefore smaller ![]() $St$).
$St$).
With respect to how 2WC might further modify preferential sampling, above and beyond the effect of ![]() $Sv$ just discussed, in figure 11 we show plots of the PDF of
$Sv$ just discussed, in figure 11 we show plots of the PDF of ![]() $\mathcal {Q}^p(t)$ for different
$\mathcal {Q}^p(t)$ for different ![]() $St$, and for the 1WC and 2WC cases. The results show that 2WC has a weak effect on these statistics, implying that the preferential sampling of the flow by the particles is only weakly affected by 2WC, at least for the
$St$, and for the 1WC and 2WC cases. The results show that 2WC has a weak effect on these statistics, implying that the preferential sampling of the flow by the particles is only weakly affected by 2WC, at least for the ![]() $\varPhi _m$ we have considered. Taken together with our previous point about the effect of
$\varPhi _m$ we have considered. Taken together with our previous point about the effect of ![]() $Sv$, this then implies that the strong reduction of preferential sampling of the flow observed by Monchaux & Dejoan (Reference Monchaux and Dejoan2017) for their lower
$Sv$, this then implies that the strong reduction of preferential sampling of the flow observed by Monchaux & Dejoan (Reference Monchaux and Dejoan2017) for their lower ![]() $\varPhi _m$ case (which is the same
$\varPhi _m$ case (which is the same ![]() $\varPhi _m$ as we consider) is not due to 2WC, but is rather due to the effect of increasing
$\varPhi _m$ as we consider) is not due to 2WC, but is rather due to the effect of increasing ![]() $Sv$. Our results in figure 7 provide convincing evidence that preferential sweeping continues to be the mechanism enhancing the particle settling even in the presence of 2WC. For larger
$Sv$. Our results in figure 7 provide convincing evidence that preferential sweeping continues to be the mechanism enhancing the particle settling even in the presence of 2WC. For larger ![]() $Sv$ (corresponding to smaller
$Sv$ (corresponding to smaller ![]() $Fr$), we expect that this will still be the case, although the preferential sweeping will take place at larger scales in the flow (as was observed for the 1WC case in Tom & Bragg (Reference Tom and Bragg2019), see figures 10 and 11). This, as well as the question of how large
$Fr$), we expect that this will still be the case, although the preferential sweeping will take place at larger scales in the flow (as was observed for the 1WC case in Tom & Bragg (Reference Tom and Bragg2019), see figures 10 and 11). This, as well as the question of how large ![]() $\varPhi _m$ must become before the preferential sweeping mechanism ceases to be effective, are important questions for investigation in future work.
$\varPhi _m$ must become before the preferential sweeping mechanism ceases to be effective, are important questions for investigation in future work.

Figure 11. DNS results for ![]() $\mathcal {P}(\mathcal {Q})$ for different
$\mathcal {P}(\mathcal {Q})$ for different ![]() $St$, and for the 1WC and 2WC cases.
$St$, and for the 1WC and 2WC cases.
The results in figure 11 show that the statistics of ![]() $\mathcal {Q}^p(t)$ are only weakly affected by 2WC. Next, in § 4.4, we explore whether this remains true also for the contributions to
$\mathcal {Q}^p(t)$ are only weakly affected by 2WC. Next, in § 4.4, we explore whether this remains true also for the contributions to ![]() $\mathcal {Q}^p(t)$ from different scales in the flow. This is important because, according to Tom & Bragg (Reference Tom and Bragg2019), it is the behaviour of
$\mathcal {Q}^p(t)$ from different scales in the flow. This is important because, according to Tom & Bragg (Reference Tom and Bragg2019), it is the behaviour of ![]() $\mathcal {Q}^p(t)$ at different scales that is relevant for the multiscale preferential sweeping mechanism.
$\mathcal {Q}^p(t)$ at different scales that is relevant for the multiscale preferential sweeping mechanism.
4.4. Effect of 2WC on preferential sampling at different scales
The preferential sweeping mechanism is based in part on the argument that inertial particles preferentially sample strain-dominated regions of the flow due to the centrifuge effect (Maxey Reference Maxey1987). To explore this preferential sampling of the flow in more detail, and its behaviour at different scales of the flow, we now introduce the invariant based on the filtered velocity gradients
where ![]() $\widetilde {\mathcal {S}}^2\equiv \widetilde {\boldsymbol {\mathcal {S}}}\boldsymbol {:}\widetilde{\boldsymbol {\mathcal {S}}}$,
$\widetilde {\mathcal {S}}^2\equiv \widetilde {\boldsymbol {\mathcal {S}}}\boldsymbol {:}\widetilde{\boldsymbol {\mathcal {S}}}$, ![]() $\widetilde {\mathcal {R}}^2\equiv \widetilde{\boldsymbol {\mathcal {R}}}\boldsymbol {:}\widetilde{\boldsymbol {\mathcal {R}}}$ and
$\widetilde {\mathcal {R}}^2\equiv \widetilde{\boldsymbol {\mathcal {R}}}\boldsymbol {:}\widetilde{\boldsymbol {\mathcal {R}}}$ and ![]() $\widetilde{\boldsymbol {\mathcal {S}}}$,
$\widetilde{\boldsymbol {\mathcal {S}}}$, ![]() $\widetilde{\boldsymbol {\mathcal {R}}}$ denote
$\widetilde{\boldsymbol {\mathcal {R}}}$ denote ![]() $\boldsymbol {\mathcal {S}}$,
$\boldsymbol {\mathcal {S}}$, ![]() $\boldsymbol {\mathcal {R}}$ coarse grained on the scale
$\boldsymbol {\mathcal {R}}$ coarse grained on the scale ![]() $\ell _F$. To compare the strength of the preferential sampling of the flow across the scales, we consider
$\ell _F$. To compare the strength of the preferential sampling of the flow across the scales, we consider
For homogeneous turbulence, ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle =0$ when measured along the trajectories of particles that do not preferentially sample the flow. The normalization involving
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle =0$ when measured along the trajectories of particles that do not preferentially sample the flow. The normalization involving ![]() $\langle [\widetilde {\mathcal {Q}}^p(t)]^2\rangle -\langle \widetilde {\mathcal {Q}}^p(t)\rangle ^2$ is used to factor out the trivial scale dependence that can arise simply because the variance of the fluid velocity gradients decreases with increasing filter scale. We also note that, since the strength of the velocity gradients increases with decreasing scale, the dominant contribution to
$\langle [\widetilde {\mathcal {Q}}^p(t)]^2\rangle -\langle \widetilde {\mathcal {Q}}^p(t)\rangle ^2$ is used to factor out the trivial scale dependence that can arise simply because the variance of the fluid velocity gradients decreases with increasing filter scale. We also note that, since the strength of the velocity gradients increases with decreasing scale, the dominant contribution to ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ would be from the smallest scales contained in the filtered velocity field,
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ would be from the smallest scales contained in the filtered velocity field, ![]() $\tilde {u}_z(\boldsymbol {x},t)$ (as opposed to
$\tilde {u}_z(\boldsymbol {x},t)$ (as opposed to ![]() $\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ which would be dominated by the large scales in the sub-grid velocity field,
$\langle u'_z(\boldsymbol {x}^p(t),t)\rangle$ which would be dominated by the large scales in the sub-grid velocity field, ![]() $u'_z(\boldsymbol {x},t)$).
$u'_z(\boldsymbol {x},t)$).
In figure 12, we show the normalized ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ across a range of scales for varying
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ across a range of scales for varying ![]() $St$ and fixed
$St$ and fixed ![]() $Re_{\lambda }$. The results show
$Re_{\lambda }$. The results show ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle >0$, indicating that the particles preferentially sample strain-dominated regions of the flow at all scales. For larger values of
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle >0$, indicating that the particles preferentially sample strain-dominated regions of the flow at all scales. For larger values of ![]() $\ell _F$ the 1WC and 2WC cases are similar, showing that 2WC has a negligible effect on preferential sampling at these scales. When we consider the effect of 2WC when the effect of all scales is included, i.e. when
$\ell _F$ the 1WC and 2WC cases are similar, showing that 2WC has a negligible effect on preferential sampling at these scales. When we consider the effect of 2WC when the effect of all scales is included, i.e. when ![]() $\ell _F/\eta \to 0$, then there is a noticeable effect, but the effect is still small. In this case, for fixed
$\ell _F/\eta \to 0$, then there is a noticeable effect, but the effect is still small. In this case, for fixed ![]() $\ell _F$, 2WC slightly reduces
$\ell _F$, 2WC slightly reduces ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ for
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ for ![]() $St < 1$ and increases
$St < 1$ and increases ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ for
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ for ![]() $St > 1$. For
$St > 1$. For ![]() $\ell _F/\eta \lesssim 10$,
$\ell _F/\eta \lesssim 10$, ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ is approximately independent of
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ is approximately independent of ![]() $\ell _F$ when
$\ell _F$ when ![]() $St < O(1)$, and then decreases for larger
$St < O(1)$, and then decreases for larger ![]() $\ell _F$. This can be explained by considering the dependence of preferential sampling on
$\ell _F$. This can be explained by considering the dependence of preferential sampling on ![]() $St_\ell$ and noting that we would expect the preferential sampling at any scale
$St_\ell$ and noting that we would expect the preferential sampling at any scale ![]() $\ell$ to be maximum for
$\ell$ to be maximum for ![]() $St_\ell =O(1)$ (Tom & Bragg Reference Tom and Bragg2019). For
$St_\ell =O(1)$ (Tom & Bragg Reference Tom and Bragg2019). For ![]() $\ell \leq O(10\eta )$, the eddy-turnover time
$\ell \leq O(10\eta )$, the eddy-turnover time ![]() $\tau _\ell$ is approximately constant, and hence so also is
$\tau _\ell$ is approximately constant, and hence so also is ![]() $St_\ell$. Since
$St_\ell$. Since ![]() $\tau _\ell$ increases with increasing
$\tau _\ell$ increases with increasing ![]() $\ell$,
$\ell$, ![]() $St_\ell$ decreases with increasing
$St_\ell$ decreases with increasing ![]() $\ell$. As such, if
$\ell$. As such, if ![]() $St< O(1)$, then
$St< O(1)$, then ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ should be approximately constant for
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ should be approximately constant for ![]() $\ell \leq O(10\eta )$ and will then decrease as
$\ell \leq O(10\eta )$ and will then decrease as ![]() $\ell$ is further increased. On the other hand, if
$\ell$ is further increased. On the other hand, if ![]() $St> O(1)$, then as
$St> O(1)$, then as ![]() $\ell$ is increased,
$\ell$ is increased, ![]() $St_\ell$ will decrease and approach
$St_\ell$ will decrease and approach ![]() $O(1)$, and then continue to reduce as
$O(1)$, and then continue to reduce as ![]() $\ell$ is further increased. In this case,
$\ell$ is further increased. In this case, ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ would have a non-monotonic behaviour, first increasing as
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ would have a non-monotonic behaviour, first increasing as ![]() $\ell$ is increased, and then decreasing, a behaviour that can be observed especially for the
$\ell$ is increased, and then decreasing, a behaviour that can be observed especially for the ![]() $St=2$ data in figure 12. This may seem inconsistent because a value of
$St=2$ data in figure 12. This may seem inconsistent because a value of ![]() $2$ is
$2$ is ![]() $O(1)$. The fact that this non-monotonic behaviour occurs for
$O(1)$. The fact that this non-monotonic behaviour occurs for ![]() $St=2$, even though it is only expected for
$St=2$, even though it is only expected for ![]() $St> O(1)$ is likely because the definition of
$St> O(1)$ is likely because the definition of ![]() $St$ (and
$St$ (and ![]() $St_\ell$) used here underestimates the effect of particle inertia, because for a settling particle the time scale of the velocity gradients seen by the particle would be smaller than that for fluid particles (Ireland et al. Reference Ireland, Bragg and Collins2016b). This is related to the discussion in § 4.3 and the importance of the alternative scale-dependent Stokes number
$St_\ell$) used here underestimates the effect of particle inertia, because for a settling particle the time scale of the velocity gradients seen by the particle would be smaller than that for fluid particles (Ireland et al. Reference Ireland, Bragg and Collins2016b). This is related to the discussion in § 4.3 and the importance of the alternative scale-dependent Stokes number ![]() $St_\ell ^*$ when considering the dynamics of settling particles in turbulence.
$St_\ell ^*$ when considering the dynamics of settling particles in turbulence.

Figure 12. Normalized ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ for the 1WC and 2WC cases shown as a function of the normalized filtering length
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ for the 1WC and 2WC cases shown as a function of the normalized filtering length ![]() $\ell _F/\eta$ for varying
$\ell _F/\eta$ for varying ![]() $St$ and fixed
$St$ and fixed ![]() $Re_{\lambda } = 87$ and
$Re_{\lambda } = 87$ and ![]() $Fr = 1$.
$Fr = 1$.
The results in figure 13 for varying ![]() $Re_{\lambda }$ and fixed
$Re_{\lambda }$ and fixed ![]() $St$ also show that 2WC has only a small effect on preferential sampling at all scales. For
$St$ also show that 2WC has only a small effect on preferential sampling at all scales. For ![]() $\ell _F=0$ (unfiltered results), the preferential sampling becomes weaker as
$\ell _F=0$ (unfiltered results), the preferential sampling becomes weaker as ![]() $Re_\lambda$ is increased, consistent with the results of Ireland et al. (Reference Ireland, Bragg and Collins2016a,Reference Ireland, Bragg and Collinsb) for
$Re_\lambda$ is increased, consistent with the results of Ireland et al. (Reference Ireland, Bragg and Collins2016a,Reference Ireland, Bragg and Collinsb) for ![]() $Fr=\infty$. For larger
$Fr=\infty$. For larger ![]() $\ell _F$, the main difference in the results is simply due to the different range of scales available for the particles to preferentially sample as
$\ell _F$, the main difference in the results is simply due to the different range of scales available for the particles to preferentially sample as ![]() $Re_\lambda$ is varied.
$Re_\lambda$ is varied.

Figure 13. Normalized ![]() $\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ for the 1WC and 2WC cases shown as a function of the normalized filtering length
$\langle \widetilde {\mathcal {Q}}^p(t)\rangle$ for the 1WC and 2WC cases shown as a function of the normalized filtering length ![]() $\ell _F/\eta$ for varying
$\ell _F/\eta$ for varying ![]() $Re_{\lambda }$ and fixed
$Re_{\lambda }$ and fixed ![]() $St = 1$ and
$St = 1$ and ![]() $Fr = 1$.
$Fr = 1$.
Referring back to the discussion surrounding equation (2.5) in § 2.3, the results for ![]() $\mathcal {Q}^p(t)$ imply that the principal way that 2WC modifies
$\mathcal {Q}^p(t)$ imply that the principal way that 2WC modifies ![]() $\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is by modifying the field
$\langle u_z(\boldsymbol {x}^p(t),t)\rangle$ is by modifying the field ![]() $u'_z(\boldsymbol {x},t)$ in the vicinity of the particles, and not by modifying the spatial distribution/preferential concentration of the particles associated with the factor
$u'_z(\boldsymbol {x},t)$ in the vicinity of the particles, and not by modifying the spatial distribution/preferential concentration of the particles associated with the factor ![]() $\exp ( -\int _0^t\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {V}}'(\boldsymbol {\mathcal {X}}(s\vert \boldsymbol {x},t),s)\,{\rm d}s)$ in (2.5).
$\exp ( -\int _0^t\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {V}}'(\boldsymbol {\mathcal {X}}(s\vert \boldsymbol {x},t),s)\,{\rm d}s)$ in (2.5).
5. Conclusions
In this paper, we have explored how 2WC affects the preferential sweeping mechanism which is responsible for the enhanced settling speeds of inertial particles in 1WC turbulent flows. Most numerical and theoretical studies on particle settling have focused on the 1WC regime, where the forcing from the particles on the flow is negligible. Maxey (Reference Maxey1987) developed a theoretical analysis to explain enhanced particle settling in 1WC homogeneous turbulence, and according to this analysis, inertial particles tend to be swept around vortices in the flow due to their inertia, and in the presence of gravity, they exhibit a tendency to be swept around the downward moving side of vortices. This tendency to preferentially sample strain-dominated regions of the flow where fluid velocity is pointing in the direction of gravity then generates enhanced settling velocities in turbulence, and is referred to as the preferential sweeping mechanism (Wang & Maxey Reference Wang and Maxey1993). However, the theoretical analysis of Maxey (Reference Maxey1987) was restricted to ![]() $St \ll 1$. In a recent work, Tom & Bragg (Reference Tom and Bragg2019) extended the analysis to arbitrary
$St \ll 1$. In a recent work, Tom & Bragg (Reference Tom and Bragg2019) extended the analysis to arbitrary ![]() $St$, which revealed the truly multiscale nature of the preferential sweeping mechanism. The analysis showed that only a restricted range of scales contribute to enhanced settling, and this range depends on particle inertia. The results also showed that the largest scale that contributes to the sweeping is much larger than previously thought. In this work, we applied our analysis to the 2WC case and using DNS demonstrated that preferential sweeping is still the mechanism generating enhanced particle settling in 2WC homogeneous turbulent flows.
$St$, which revealed the truly multiscale nature of the preferential sweeping mechanism. The analysis showed that only a restricted range of scales contribute to enhanced settling, and this range depends on particle inertia. The results also showed that the largest scale that contributes to the sweeping is much larger than previously thought. In this work, we applied our analysis to the 2WC case and using DNS demonstrated that preferential sweeping is still the mechanism generating enhanced particle settling in 2WC homogeneous turbulent flows.
Our DNS considered a volume fraction of ![]() $\varPhi _v=1.5\times 10^{-5}$ in order to explore the regime where the effect of 2WC on the global fluid statistics is weak, but where 2WC may nevertheless be important for the particle settling. In agreement with previous results for a similar region (Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Monchaux & Dejoan Reference Monchaux and Dejoan2017; Rosa et al. Reference Rosa, Kopeć, Ababaei and Pozorski2021), our results show that 2WC can lead to particle settling enhancements that are more than twice those in the corresponding 1WC case, even though
$\varPhi _v=1.5\times 10^{-5}$ in order to explore the regime where the effect of 2WC on the global fluid statistics is weak, but where 2WC may nevertheless be important for the particle settling. In agreement with previous results for a similar region (Bosse et al. Reference Bosse, Kleiser and Meiburg2006; Monchaux & Dejoan Reference Monchaux and Dejoan2017; Rosa et al. Reference Rosa, Kopeć, Ababaei and Pozorski2021), our results show that 2WC can lead to particle settling enhancements that are more than twice those in the corresponding 1WC case, even though ![]() $\varPhi _v$ is small. This is an important point since the effects of 2WC are traditionally ignored in weather forecasting models that parameterize particle settling through the atmosphere (Kukkonen et al. Reference Kukkonen2012) upon the assumption that
$\varPhi _v$ is small. This is an important point since the effects of 2WC are traditionally ignored in weather forecasting models that parameterize particle settling through the atmosphere (Kukkonen et al. Reference Kukkonen2012) upon the assumption that ![]() $\varPhi _v$ is sufficiently small in those contexts. As emphasized in Monchaux & Dejoan (Reference Monchaux and Dejoan2017), the key point is that even if
$\varPhi _v$ is sufficiently small in those contexts. As emphasized in Monchaux & Dejoan (Reference Monchaux and Dejoan2017), the key point is that even if ![]() $\varPhi _v$ is small enough for the particles to not affect the global fluid statistics, it may be strong enough to significantly modify the flow in the vicinity of the particles, which in turn modifies the particle motion. Moreover, recent field experiments (Li et al. Reference Li, Lim, Berk, Abraham, Heisel, Guala, Coletti and Hong2021a) suggest that turbulence is a key factor influencing the fall speed of snow through the atmosphere, which in turn influences local hydrology and vegetation development (Lehning et al. Reference Lehning, Löwe, Ryser and Raderschall2008). Hence, a detailed understanding of the physical mechanisms responsible for settling enhancement and the impact of 2WC is important not only from a fundamental physics perspective, but also for developing accurate parametrizations of particle settling in atmospheric and weather forecasting models.
$\varPhi _v$ is small enough for the particles to not affect the global fluid statistics, it may be strong enough to significantly modify the flow in the vicinity of the particles, which in turn modifies the particle motion. Moreover, recent field experiments (Li et al. Reference Li, Lim, Berk, Abraham, Heisel, Guala, Coletti and Hong2021a) suggest that turbulence is a key factor influencing the fall speed of snow through the atmosphere, which in turn influences local hydrology and vegetation development (Lehning et al. Reference Lehning, Löwe, Ryser and Raderschall2008). Hence, a detailed understanding of the physical mechanisms responsible for settling enhancement and the impact of 2WC is important not only from a fundamental physics perspective, but also for developing accurate parametrizations of particle settling in atmospheric and weather forecasting models.
Next, we explored in detail how 2WC modifies the contribution from different scales of the flow to the turbulence-induced enhancement of the particle settling velocities by considering the contribution of scales of size ![]() $<\ell _F$ (i.e. sub-grid velocity field) to the particle settling velocity. The results showed that, at the smallest scales of the flow, 2WC very strongly enhances the contribution of these scales to the particle settling velocity, with the impact of 2WC decreasing as
$<\ell _F$ (i.e. sub-grid velocity field) to the particle settling velocity. The results showed that, at the smallest scales of the flow, 2WC very strongly enhances the contribution of these scales to the particle settling velocity, with the impact of 2WC decreasing as ![]() $\ell _F$ is increased, but still remaining significant for
$\ell _F$ is increased, but still remaining significant for ![]() $\ell _F$ approaching the largest scales of the flow. By also considering the second moment of the sub-grid fluid velocity at the particle positions for the 1WC and 2WC cases, we concluded that this strong enhancement due to 2WC is plausibly explained in terms of the fluid dragging effect described by Monchaux & Dejoan (Reference Monchaux and Dejoan2017). According to this effect, the settling inertial particles on average accelerate the flow in their vicinity in the direction of gravity, which causes the fluid velocity in their vicinity to be increased compared with the 1WC case.
$\ell _F$ approaching the largest scales of the flow. By also considering the second moment of the sub-grid fluid velocity at the particle positions for the 1WC and 2WC cases, we concluded that this strong enhancement due to 2WC is plausibly explained in terms of the fluid dragging effect described by Monchaux & Dejoan (Reference Monchaux and Dejoan2017). According to this effect, the settling inertial particles on average accelerate the flow in their vicinity in the direction of gravity, which causes the fluid velocity in their vicinity to be increased compared with the 1WC case.
To understand the role being played by the preferential sweeping mechanism in the 2WC case, and whether its effect is being suppressed or even eradicated due to the fluid dragging effect, as suggested by Monchaux & Dejoan (Reference Monchaux and Dejoan2017), we considered the average fluid velocity at the particle position conditioned on the local flow structure. Consistent with the preferential sweeping mechanism, the results showed that the average fluid velocity at the particle position (which is the term that quantifies the enhanced particle settling due to turbulence) is dominated by contributions where the particles are located in strain-dominated regions of the flow. This is, however, enhanced in the 2WC case due to the fluid dragging effect. Therefore, rather than 2WC eliminating the importance of preferential sweeping, what actually occurs is more subtle. In particular, for both 1WC and 2WC flows, the settling enhancement due to turbulence is dominated by contributions from particles in strain-dominated regions of the flow, but for the 2WC case, in these strain-dominated regions the particles also drag the fluid with them, increasing the local fluid velocity and hence leading to further enhancement of the particle settling due to turbulence. Note that the particles also drag the fluid down with them when they are in rotation-dominated regions, but again, the contribution from particles in strain-dominated regions dominates the settling behaviour, consistent with the preferential sweeping mechanism.
We present an alternate interpretation for the results in Monchaux & Dejoan (Reference Monchaux and Dejoan2017) regarding the effectiveness of the preferential sweeping mechanism in 2WC flows. As shown in Tom & Bragg (Reference Tom and Bragg2019), when the particle settling number ![]() $Sv$ increases, the particles begin to preferentially sample the small scales less and larger scales more since settling reduces the eddy-turnover time scales seen by the particles. For sufficiently large
$Sv$ increases, the particles begin to preferentially sample the small scales less and larger scales more since settling reduces the eddy-turnover time scales seen by the particles. For sufficiently large ![]() $Sv$, even though particles do not preferentially sample the unfiltered fluid velocity gradient field, they do preferentially sample the fluid velocity gradient field at some finite filter length
$Sv$, even though particles do not preferentially sample the unfiltered fluid velocity gradient field, they do preferentially sample the fluid velocity gradient field at some finite filter length ![]() $\ell _F$. Hence, the fact that Monchaux & Dejoan (Reference Monchaux and Dejoan2017) did not observe preferential sampling of the unfiltered velocity gradients does not imply that the preferential sweeping was ineffective in their 2WC DNS. To observe the preferential sampling in their flow they would have needed to consider the statistics of the filtered fluid velocity gradient along the inertial particle trajectory. Further supporting this argument is that our results for the PDF and average of the second invariant of fluid velocity gradients sampled by the inertial particles reveals a weak influence of 2WC on these quantities.
$\ell _F$. Hence, the fact that Monchaux & Dejoan (Reference Monchaux and Dejoan2017) did not observe preferential sampling of the unfiltered velocity gradients does not imply that the preferential sweeping was ineffective in their 2WC DNS. To observe the preferential sampling in their flow they would have needed to consider the statistics of the filtered fluid velocity gradient along the inertial particle trajectory. Further supporting this argument is that our results for the PDF and average of the second invariant of fluid velocity gradients sampled by the inertial particles reveals a weak influence of 2WC on these quantities.
In summary, our results reveal that for the ![]() $\varPhi _v$ considered, 2WC enhances the particle settling velocities compared with the 1WC case by strongly modifying the fluid velocity in the vicinity of the particles, while only weakly affecting the preferential sampling of the velocity gradients by the inertial particles. As such, these results reveal that the multiscale preferential sweeping continues to be the mechanism by which turbulence enhances the settling of inertial particles in 2WC homogeneous turbulent flows. Important issues for future investigation are how these conclusions might change for larger particle mass loadings, and for smaller Froude numbers.
$\varPhi _v$ considered, 2WC enhances the particle settling velocities compared with the 1WC case by strongly modifying the fluid velocity in the vicinity of the particles, while only weakly affecting the preferential sampling of the velocity gradients by the inertial particles. As such, these results reveal that the multiscale preferential sweeping continues to be the mechanism by which turbulence enhances the settling of inertial particles in 2WC homogeneous turbulent flows. Important issues for future investigation are how these conclusions might change for larger particle mass loadings, and for smaller Froude numbers.
Finally, it is important to consider the implications of our findings for modelling the transport of settling particles using large-eddy simulations (LES). In LES, the flow is only resolved down to a filter scale ![]() $\ell _F$, and typically
$\ell _F$, and typically ![]() $\ell _F\gg \eta$ such that the LES is computationally much cheaper than a DNS. For any particle processes that depend significantly on the flow motion at scales
$\ell _F\gg \eta$ such that the LES is computationally much cheaper than a DNS. For any particle processes that depend significantly on the flow motion at scales ![]() $\ell <\ell _F$, it is important to include in the particle equation of motion a particle sub-grid model (PSGM) (Ray & Collins Reference Ray and Collins2011), which is a model for the unresolved (sub-grid) fluid velocity at
$\ell <\ell _F$, it is important to include in the particle equation of motion a particle sub-grid model (PSGM) (Ray & Collins Reference Ray and Collins2011), which is a model for the unresolved (sub-grid) fluid velocity at ![]() $\ell <\ell _F$ seen by the particles. According to the theory presented in Tom & Bragg (Reference Tom and Bragg2019), the particle settling velocity is influenced by scales up to
$\ell <\ell _F$ seen by the particles. According to the theory presented in Tom & Bragg (Reference Tom and Bragg2019), the particle settling velocity is influenced by scales up to ![]() $\ell _c(St)$, and as discussed previously, this is also the maximum scale at which 2WC affects the flow. If the LES has
$\ell _c(St)$, and as discussed previously, this is also the maximum scale at which 2WC affects the flow. If the LES has ![]() $\ell _F\geq \ell _c(St)$, then all of the complex processes governing the particle settling (multiscale preferential sweeping and the impact of 2WC) will have to be described by the PSGM. However, even for a 1WC case, developing accurate PSGMs is very challenging (Ray & Collins Reference Ray and Collins2014), and therefore one would usually wish to minimize the extent to which the PSGM contributes to the particle motion in the LES model, requiring an appropriate choice of
$\ell _F\geq \ell _c(St)$, then all of the complex processes governing the particle settling (multiscale preferential sweeping and the impact of 2WC) will have to be described by the PSGM. However, even for a 1WC case, developing accurate PSGMs is very challenging (Ray & Collins Reference Ray and Collins2014), and therefore one would usually wish to minimize the extent to which the PSGM contributes to the particle motion in the LES model, requiring an appropriate choice of ![]() $\ell _F$. Using K41 scaling together with DNS data we estimated in Tom & Bragg (Reference Tom and Bragg2019) that
$\ell _F$. Using K41 scaling together with DNS data we estimated in Tom & Bragg (Reference Tom and Bragg2019) that ![]() $\ell _c(St)\sim \eta (St/\gamma )^{3/2}$, with
$\ell _c(St)\sim \eta (St/\gamma )^{3/2}$, with ![]() $\gamma \approx 7\times 10^{-4}$. If
$\gamma \approx 7\times 10^{-4}$. If ![]() $St\geq O(10^{-2})$, then
$St\geq O(10^{-2})$, then ![]() $\ell _c(St)\gg \eta$, and so the LES may resolve
$\ell _c(St)\gg \eta$, and so the LES may resolve ![]() $\ell _c(St)$. However, given the definition of
$\ell _c(St)$. However, given the definition of ![]() $\ell _c(St)$, if the PSGM is to only play a sub-leading role in the LES model for particle transport, then the LES should resolve down to scales where
$\ell _c(St)$, if the PSGM is to only play a sub-leading role in the LES model for particle transport, then the LES should resolve down to scales where ![]() $St_\ell =O(1)$, and this scale will usually be much smaller than
$St_\ell =O(1)$, and this scale will usually be much smaller than ![]() $\ell _c(St)$. Clearly, for particles with
$\ell _c(St)$. Clearly, for particles with ![]() $St=O(1)$, this presents a problem since then the scale at which
$St=O(1)$, this presents a problem since then the scale at which ![]() $St_\ell =O(1)$ is
$St_\ell =O(1)$ is ![]() $\ell =O(\eta )$, and so the LES would require the same resolution as DNS. Only if
$\ell =O(\eta )$, and so the LES would require the same resolution as DNS. Only if ![]() $St\gg O(1)$ will
$St\gg O(1)$ will ![]() $St_\ell =O(1)$ be satisfied for
$St_\ell =O(1)$ be satisfied for ![]() $\ell \gg \eta$. This then presents a major challenge for using LES to model the settling of particles with
$\ell \gg \eta$. This then presents a major challenge for using LES to model the settling of particles with ![]() $St=O(1)$ since if the LES is to use a filter length
$St=O(1)$ since if the LES is to use a filter length ![]() $\ell _F\gg \eta$, then the PSGM must be sufficiently sophisticated to be able to capture both the spatio-temporal flow properties underlying the multiscale preferential sweeping mechanism, as well as the impact of 2WC on these flow properties.
$\ell _F\gg \eta$, then the PSGM must be sufficiently sophisticated to be able to capture both the spatio-temporal flow properties underlying the multiscale preferential sweeping mechanism, as well as the impact of 2WC on these flow properties.
In addition to these complexities surrounding models for the PSGM, the fluid SGM used in the LES itself must also include the effect of 2WC, and the present results, as well as those of Bosse et al. (Reference Bosse, Kleiser and Meiburg2006) and Monchaux & Dejoan (Reference Monchaux and Dejoan2017), indicate that the effect of 2WC on fluid subgrid-scale (SGS) models needs to be captured even for low mass loadings. In particular, the fluid SGS model should be able to capture the fact that the fluid velocities in the particle vicinity may be strongly modified due to 2WC, even if the global fluid properties are weakly affected by 2WC. It would be interesting to see the extent to which dynamic SGS models, e.g. similar to the dynamic Smagorinsky model (Germano et al. Reference Germano, Piomelli, Moin and Cabot1991; Pope Reference Pope2000), could capture this local effect.
Acknowledgements
A.D.B. gratefully acknowledges enlightening conversations with JAK Horwitz on the subject of two-way coupling in the context of point-particle models. The authors also gratefully acknowledge S. Bhattacharjee for carefully reading through the manuscript and providing helpful feedback.
Funding
This work was supported by the National Aeronautics and Space Administration's Weather and Atmospheric Dynamics program (grant number NASA 80NSSC20K0912). The computational resources used were provided by the Extreme Science and Engineering Discovery Environment (XSEDE) under allocation CTS170009, which is supported by National Science Foundation (NSF) grant number ACI-1548562 (Towns et al. Reference Towns2014). Specifically, the Expanse cluster operated by San Diego Supercomputer Center (SDSC) was used to obtain the results in this work. The Duke Computing Cluster (DCC) operated by Duke University Research Computing was also used to obtain some of the preliminary results for this study.
Declaration of interests
The authors report no conflict of interest.