Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-03T20:31:18.207Z Has data issue: false hasContentIssue false
  • English
  • Français

High-mode stationary waves in stratified flow over large obstacles

Published online by Cambridge University Press:  11 February 2010

JODY M. KLYMAK ,
SONYA M. LEGG  and
ROBERT PINKEL
JODY M. KLYMAK*
Affiliation:
Department of Physics and Astronomy, University of Victoria, Victoria, Canada, V8W 3P6
SONYA M. LEGG
Affiliation:
Program in Atmosphere and Ocean Sciences, Princeton University, Princeton, NJ 08544, USA
ROBERT PINKEL
Affiliation:
Scripps Institution of Oceanography, University of California, San Diego, La Jolla, CA 98105, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Simulations of steady two-dimensional stratified flow over an isolated obstacle are presented where the obstacle is tall enough so that the topographic Froude number, Nhm/Uo ≫ 1. N is the buoyancy frequency, hm the height of the topography from the channel floor and Uo the flow speed infinitely far from the obstacle. As for moderate Nhm/Uo (~1), a columnar response propagates far up- and downstream, and an arrested lee wave forms at the topography. Upstream, most of the water beneath the crest is blocked, while the moving layer above the crest has a mean velocity Um = UoH/(H−hm). The vertical wavelength implied by this velocity scale, λo = 2πUm/N, predicts dominant vertical scales in the flow. Upstream of the crest there is an accelerated region of fluid approximately λo thick, above which there is a weakly oscillatory flow. Downstream the accelerated region is thicker and has less intense velocities. Similarly, the upstream lift of isopycnals is greatest in the first wavelength near the crest, and weaker above and below. Form drag on the obstacle is dominated by the blocked response, and not on the details of the lee wave, unlike flows with moderate Nhm/Uo.

Directly downstream, the lee wave that forms has a vertical wavelength given by λo, except for the deepest lobe which tends to be thicker. This wavelength is small relative to the fluid depth and topographic height, and has a horizontal phase speed cpx = −Um, corresponding to an arrested lee wave. When considering the spin-up to steady state, the speed of vertical propagation scales with the vertical component of group velocity cgz = αUm, where α is the aspect ratio of the topography. 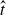This implies a time scale = tNα/2π for the growth of the lee waves, and that steady state is attained more rapidly with steep topography than shallow, in contrast with linear theory, which does not depend on the aspect ratio.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 644 , 10 February 2010 , pp. 321 - 336
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Afanasyev, Y. D. & Peltier, W. R. 2001 On breaking internal waves over the sill in Knight Inlet. Proc. R. Soc. Lond. A 157 (1–27).Google Scholar
Armi, L. 1986 The hydraulics of two layers with different densities. J. Fluid Mech. 163, 27–58.CrossRefGoogle Scholar
Baines, P. G. 1988 A general method for determining upstream effects in stratified flow of finite depth over a long two-dimensional obstacle. J. Fluid Mech. 188, 1–22.CrossRefGoogle Scholar
Baines, P. G. 1995 Topographic Effects in Stratified Flows. Cambridge University Press.Google Scholar
Bell, T. H. 1975 Lee waves in stratified flows with simple harmonic time dependence. J. Fluid Mech. 67, 705–722.CrossRefGoogle Scholar
Chen, C.-C., Durran, D. R. & Hakim, G. J. 2005 Mountain-wave momentum flux in an evolving synoptic-scale flow. J. Atmos. Sci. 62, 3213–3231.CrossRefGoogle Scholar
Durran, D. R. 1990 Mountain waves and downslope winds. In Atmospheric Processes Over Complex Terrain, Meteorological Monographs (ed. Blumen, W.), vol. 23, pp. 59–81. American Meteorological Society.CrossRefGoogle Scholar
Farmer, D. M. & Armi, L. 1999 Stratified flow over topography: the role of small scale entrainment and mixing in flow establishment. Proc. R. Soc. Lond. Ser. A 455, 3221–3258.CrossRefGoogle Scholar
Farmer, D. M. & Denton, R. A. 1985 Hydraulic control of flow over the sill in Observatory Inlet. J. Geophys. Res. 90 (C5), 9051–9068.CrossRefGoogle Scholar
Farmer, D. M. & Smith, J. D. 1980 Tidal interaction of stratified flow with a sill in Knight Inlet. Deep Sea Res. A 27, 239–245.CrossRefGoogle Scholar
Henderson, F. M. 1966 Open Channel Hydraulics. Macmillan.Google Scholar
Inall, M. E., Rippeth, T., Griffiths, C. & Wiles, P. 2005 Evolution and distribution of tke production and dissipation within stratified flow over topography. Geophys. Res. Lett. 32, L08607, doi:10.1029/2004GL022289.CrossRefGoogle Scholar
Klymak, J. M. & Gregg, M. C. 2003 The role of upstream waves and a downstream density-pool in the growth of lee-waves: stratified flow over the Knight Inlet sill. J. Phys. Oceanogr. 33 (7), 1446–1461.2.0.CO;2>CrossRefGoogle Scholar
Klymak, J. M. & Gregg, M. C. 2004 Tidally generated turbulence over the Knight Inlet sill. J. Phys. Oceanogr. 34 (5), 1135–1151.2.0.CO;2>CrossRefGoogle Scholar
Klymak, J. M., Pinkel, R. & Rainville, L. 2008 Direct breaking of the internal tide near topography: Kaena Ridge, Hawaii. J. Phys. Oceanogr. 38, 380–399.CrossRefGoogle Scholar
Lamb, K. G. 2004 On boundary layer separation and internal wave generation at the Knight Inlet sill. Proc. R. Soc. Lond. A 460, 2305–2337.CrossRefGoogle Scholar
Legg, S. & Klymak, J. M. 2008 Internal hydrualic jumps and overturning generated by tidal flow over a steep ridge. J. Phys. Oceanogr. 38, 1949–1964.CrossRefGoogle Scholar
Levine, M. D. & Boyd, T. J. 2006 Tidally-forced internal waves and overturns observed on a slope: results from the HOME survey component. J. Phys. Oceanogr. 36, 1184–1201.CrossRefGoogle Scholar
Lilly, D. K. 1978 A severe downslope windstorm and aircraft turbulent event induced by a mountain wave. J. Atmos. Sci. 35, 59–77.2.0.CO;2>CrossRefGoogle Scholar
Long, R. R. 1955 Some aspects of the flow of stratified fluids. III. Continuous density gradients. Tellus 7, 341–357.Google Scholar
Marshall, J., Adcroft, A., Hill, C., Perelman, L. & Heisey, C. 1997 A finite-volume, incompressible Navier–Stokes model for studies of the ocean on parallel computers. J. Geophys. Res. 102 (C3), 5753–5766.CrossRefGoogle Scholar
Mellor, G. L. & Yamada, T. 1982 Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 20, 851–875.CrossRefGoogle Scholar
Miller, P. P. & Durran, D. R. 1991 On the sensitivity of downslope windstorms to the asymmetry of the mountain profile. J. Atmos. Sci. 48, 1457–1473.2.0.CO;2>CrossRefGoogle Scholar
Nash, J. D., Alford, M. H., Kunze, E., Martini, K. & Kelley, S. 2007 Hotspots of deep ocean mixing on the oregon continental slope. Geophys. Res. Lett. 34, L01605, doi:10.1029/2006GL028170.CrossRefGoogle Scholar
Orlanski, I. 1976 A simple boundary condition for unbounded hyperbolic flows. J. Comput. Phys. 21, 251–269.CrossRefGoogle Scholar
Peltier, W. R. & Clark, T. L. 1979 The evolution of finite-amplitude waves. Part II. Surface wave drag and severe downslope windstorms. J. Atmos. Sci. 36, 1498–1529.2.0.CO;2>CrossRefGoogle Scholar
Peltier, W. R. & Scinocca, J. F. 1990 The origin of severe downslope windstorm pulsation. J. Atmos. Sci. 46, 2885–2914.Google Scholar
Pierrehumbert, R. T. & Wyman, B. 1985 Upstream effects of mesoscale mountains. J. Atmos. Sci. 42 (10), 977–1003.2.0.CO;2>CrossRefGoogle Scholar
Stommel, H. & Farmer, H. G. 1953 Control of salinity in an estuary by a transition. J. Mar. Res. 12 (1), 13–20.Google Scholar