Published online by Cambridge University Press: 04 March 2015
Studying the nature of transient reflections of shock waves from surfaces is important in many engineering fields, e.g. blast protection, supersonic flights, shock focusing, medical and industrial applications and more. The recent advancements in this field reveal that the major obstacle in better understanding this phenomenon by means of experimental investigations is the limited temporal and spatial resolution. An alternative approach to commonly used high-speed photography is based on the use of a single-lens reflex (SLR) camera that captures only one image per experiment. Using this method to study a transient reflection process necessitates repeating each experiment many times while retaining extremely high repeatability. In the present study, we present a solution to this obstacle by means of a fully automated shock tube facility, which has been developed in the course of this study. A typical experiment can be executed a few hundred times with a repeatability of less than 0.01 in the incident-shock-wave Mach number at moderate shock strengths (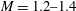 $M=1.2{-}1.4$). The system offers a very high spatial and temporal resolution description of the transient reflection process of a shock wave over a coupled convex–concave surface. The study of this complex configuration using a fully automated shock tube enables one to observe, in greater detail than ever before, both the transient transition from regular reflection, RR, to Mach reflection, MR, and the reverse transient transition from MR to RR. The geometry studied can also be found in blunt leading-edge reflectors in which higher pressures were recorded, and the results presented also describe in detail the shock reflection process inside such a reflector. The results highlight and strengthen the recent understanding of the importance of high spatial and temporal resolution in determining the transition process from RR to MR over a coupled concave–convex surface. However, despite achieving very high statistical certainty in the experimental measurements, the question of the difference between the pseudo-steady transition criterion and the experimental results remains unresolved.
$M=1.2{-}1.4$). The system offers a very high spatial and temporal resolution description of the transient reflection process of a shock wave over a coupled convex–concave surface. The study of this complex configuration using a fully automated shock tube enables one to observe, in greater detail than ever before, both the transient transition from regular reflection, RR, to Mach reflection, MR, and the reverse transient transition from MR to RR. The geometry studied can also be found in blunt leading-edge reflectors in which higher pressures were recorded, and the results presented also describe in detail the shock reflection process inside such a reflector. The results highlight and strengthen the recent understanding of the importance of high spatial and temporal resolution in determining the transition process from RR to MR over a coupled concave–convex surface. However, despite achieving very high statistical certainty in the experimental measurements, the question of the difference between the pseudo-steady transition criterion and the experimental results remains unresolved.
Equally contributed authors.