Published online by Cambridge University Press: 17 December 2015
We report on the enhancement of turbulent convective heat transport due to vapour-bubble nucleation at the bottom plate of a cylindrical Rayleigh–Bénard sample (aspect ratio 1.00, diameter 8.8 cm) filled with liquid. Microcavities acted as nucleation sites, allowing for well-controlled bubble nucleation. Only the central part of the bottom plate with a triangular array of microcavities (etched over an area with diameter of 2.5 cm) was heated. We studied the influence of the cavity density and of the superheat 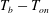 $T_{b}-T_{on}$ (
$T_{b}-T_{on}$ (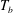 $T_{b}$ is the bottom-plate temperature and
$T_{b}$ is the bottom-plate temperature and 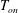 $T_{on}$ is the value of
$T_{on}$ is the value of 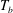 $T_{b}$ below which no nucleation occurred). The effective thermal conductivity, as expressed by the Nusselt number
$T_{b}$ below which no nucleation occurred). The effective thermal conductivity, as expressed by the Nusselt number 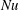 $\mathit{Nu}$, was measured as a function of the superheat by varying
$\mathit{Nu}$, was measured as a function of the superheat by varying 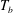 $T_{b}$ and keeping a fixed difference
$T_{b}$ and keeping a fixed difference 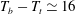 $T_{b}-T_{t}\simeq 16$ K (
$T_{b}-T_{t}\simeq 16$ K (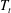 $T_{t}$ is the top-plate temperature). Initially
$T_{t}$ is the top-plate temperature). Initially 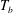 $T_{b}$ was much larger than
$T_{b}$ was much larger than 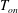 $T_{on}$ (large superheat), and the cavities vigorously nucleated vapour bubbles, resulting in two-phase flow. Reducing
$T_{on}$ (large superheat), and the cavities vigorously nucleated vapour bubbles, resulting in two-phase flow. Reducing 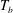 $T_{b}$ in steps until it was below
$T_{b}$ in steps until it was below 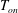 $T_{on}$ resulted in cavity deactivation, i.e. in one-phase flow. Once all cavities were inactive,
$T_{on}$ resulted in cavity deactivation, i.e. in one-phase flow. Once all cavities were inactive, 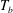 $T_{b}$ was increased again, but they did not reactivate. This led to one-phase flow for positive superheat. The heat transport of both one- and two-phase flow under nominally the same thermal forcing and degree of superheat was measured. The Nusselt number of the two-phase flow was enhanced relative to the one-phase system by an amount that increased with increasing
$T_{b}$ was increased again, but they did not reactivate. This led to one-phase flow for positive superheat. The heat transport of both one- and two-phase flow under nominally the same thermal forcing and degree of superheat was measured. The Nusselt number of the two-phase flow was enhanced relative to the one-phase system by an amount that increased with increasing 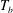 $T_{b}$. Varying the cavity density (69, 32, 3.2, 1.2 and
$T_{b}$. Varying the cavity density (69, 32, 3.2, 1.2 and 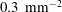 $0.3~\text{mm}^{-2}$) had only a small effect on the global
$0.3~\text{mm}^{-2}$) had only a small effect on the global 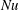 $\mathit{Nu}$ enhancement; it was found that
$\mathit{Nu}$ enhancement; it was found that 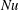 $\mathit{Nu}$ per active site decreased as the cavity density increased. The heat-flux enhancement of an isolated nucleating site was found to be limited by the rate at which the cavity could generate bubbles. Local bulk temperatures of one- and two-phase flows were measured at two positions along the vertical centreline. Bubbles increased the liquid temperature (compared to one-phase flow) as they rose. The increase was correlated with the heat-flux enhancement. The temperature fluctuations, as well as local thermal gradients, were reduced (relative to one-phase flow) by the vapour bubbles. Blocking the large-scale circulation around the nucleating area, as well as increasing the effective buoyancy of the two-phase flow by thermally isolating the liquid column above the heated area, increased the heat-flux enhancement.
$\mathit{Nu}$ per active site decreased as the cavity density increased. The heat-flux enhancement of an isolated nucleating site was found to be limited by the rate at which the cavity could generate bubbles. Local bulk temperatures of one- and two-phase flows were measured at two positions along the vertical centreline. Bubbles increased the liquid temperature (compared to one-phase flow) as they rose. The increase was correlated with the heat-flux enhancement. The temperature fluctuations, as well as local thermal gradients, were reduced (relative to one-phase flow) by the vapour bubbles. Blocking the large-scale circulation around the nucleating area, as well as increasing the effective buoyancy of the two-phase flow by thermally isolating the liquid column above the heated area, increased the heat-flux enhancement.
In some cases larger bubbles stayed at the surface for longer times. These stable larger bubbles were only observed for smaller superheat values (see figures 5 and 18), and their total number increased as superheat was reduced. This is in accordance with the observation that they formed at the edge of the heated area for larger superheat values and, for smaller superheats, eventually also within the heated area. A large bubble can presumably only be sustained if the neighboring sites are not very active. At low heat flux rates or low superheat values, the growth of a large bubble might locally cool the wafer surface around it, causing the neighboring sites to slow down at their bubble production until the temperature of the surface can be reestablished and bubble nucleation can take place at a larger rate again.
In some cases larger bubbles stayed at the surface for longer times. These stable larger bubbles were only observed for smaller superheat values (see figures 5 and 18), and their total number increased as superheat was reduced. This is in accordance with the observation that they formed at the edge of the heated area for larger superheat values and, for smaller superheats, eventually also within the heated area. A large bubble can presumably only be sustained if the neighboring sites are not very active. At low heat flux rates or low superheat values, the growth of a large bubble might locally cool the wafer surface around it, causing the neighboring sites to slow down at their bubble production until the temperature of the surface can be reestablished and bubble nucleation can take place at a larger rate again.
Shown are growing vapour-bubbles on a wafer with cavity separation of 0.6 mm and bottom plate superheat of 9.6 K. The movie was recorded at 500 fps and was slowed down 20 times for display. The area of view is a section of the etched area. Often a detaching bubble perturbed the surrounding liquid, affecting in turn the growing bubbles near by, which showed oscillations around their locations without detaching. Once the bubbles departed from the surface they were dragged by the large-scale circulation in one direction and in some cases they merged with other bubbles. After detachment the bubbles moved horizontally about 2 cm before becoming out of focus due to their rising motion.
Shown are growing vapour-bubbles on a wafer with cavity separation of 0.6 mm and bottom plate superheat of 9.6 K. The movie was recorded at 500 fps and was slowed down 20 times for display. The area of view is a section of the etched area. Often a detaching bubble perturbed the surrounding liquid, affecting in turn the growing bubbles near by, which showed oscillations around their locations without detaching. Once the bubbles departed from the surface they were dragged by the large-scale circulation in one direction and in some cases they merged with other bubbles. After detachment the bubbles moved horizontally about 2 cm before becoming out of focus due to their rising motion.