Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-20T12:32:46.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat transport by turbulent rotating Rayleigh–Bénard convection and its dependence on the aspect ratio

Published online by Cambridge University Press:  02 September 2011

Stephan Weiss  and
Guenter Ahlers
Stephan Weiss
Affiliation:
Department of Physics, University of California, Santa Barbara, CA 93106, USA
Guenter Ahlers*
Affiliation:
Department of Physics, University of California, Santa Barbara, CA 93106, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

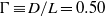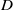We report on the influence of rotation about a vertical axis on heat transport by turbulent Rayleigh–Bénard convection in a cylindrical vessel with an aspect ratio ( is the diameter and 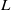the height of the sample) and compare the results with those for larger 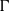. The working fluid was water at 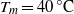where the Prandtl number  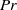is 4.38. For rotation rates 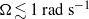, corresponding to inverse Rossby numbers 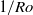between zero and twenty, we measured the Nusselt number 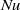for six Rayleigh numbers 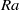in the range 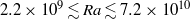. For small rotation rates and at constant 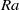, the reduced Nusselt number 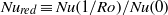initially increased slightly with increasing 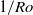, but at 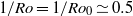it suddenly became constant or decreased slightly depending on 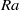. At 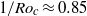a second sharp transition occurred in 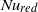to a state where 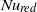increased with increasing . We know from direct numerical simulation that the transition at 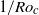corresponds to the onset of Ekman vortex formation reported before for 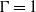at 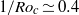and for 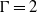at 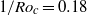(Weiss et al., Phys. Rev. Lett., vol. 105, 2010, 224501). The 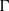-dependence of 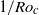can be explained as a finite-size effect that can be described phenomenologically by a Ginzburg–Landau model; this model is discussed in detail in the present paper. We do not know the origin of the transition at 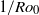. Above 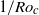, 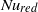increased with increasing 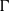up to 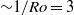. We discuss the 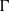-dependence of 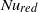in this range in terms of the average Ekman vortex density as predicted by the model. At even larger 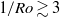there is a decrease of 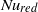that can be attributed to two possible effects. First, the Ekman pumping might become less efficient when the Ekman layer is significantly smaller than the thermal boundary layer, and second, for rather large 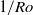, the Taylor–Proudman effect in combination with boundary conditions suppresses fluid flow in the vertical direction.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Convection: Buoyancy-driven instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 684 , 10 October 2011 , pp. 407 - 426
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abramowitz, M. & Stegun, I. A. 1970 Handbook of Mathematical Functions. Dover.Google Scholar
2. Ahlers, G. 2000 Effect of sidewall conductance on heat-transport measurements for turbulent Rayleigh–Bénard convection. Phys. Rev. E 63, R015303.CrossRefGoogle ScholarPubMed
3. Ahlers, G. 2009 Turbulent convection. Physics 2, 74.CrossRefGoogle Scholar
4. Ahlers, G., Brown, E. & Nikolaenko, A. 2006 The search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 557, 347–367.CrossRefGoogle Scholar
5. Ahlers, G., Calzavarini, E., Fontenele Araujo, F., Funfschilling, D., Grossmann, S., Lohse, D. & Sugiyama, K. 2008 Non-Oberbeck–Boussinesq effects in turbulent thermal convection in ethane close to the critical point. Phys. Rev. E 77, 046302.CrossRefGoogle Scholar
6. Ahlers, G., Cross, M. C., Hohenberg, P. C. & Safran, S. 1981 The amplitude equation near the convective threshold: application to time-dependent experiments. J. Fluid Mech. 110, 297–334.CrossRefGoogle Scholar
7. Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–538.CrossRefGoogle Scholar
8. Bailon-Cuba, J., Emran, M. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
9. Bak, P., Tang, C. & Wiesenfeld, K. 1988 Self-organized criticality. Phys. Rev. A 38, 364–374.CrossRefGoogle ScholarPubMed
10. Brown, E., Nikolaenko, A., Funfschilling, D. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection: effect of finite top- and bottom-plate conductivity. Phys. Fluids 17, 075108.CrossRefGoogle Scholar
11. Buell, J. C. & Catton, I. 1983 The effect of wall conduction on the stability of a fluid in a right circular-cylinder heated from below. Trans. ASME: J. Heat Transfer 105, 255–260.CrossRefGoogle Scholar
12. Busse, F. H. 1978 Nonlinear properties of convection. Rep. Prog. Phys. 41, 1926–1967.CrossRefGoogle Scholar
13. Cattaneo, F., Emonet, T. & Weiss, N. 2003 On the interaction between convection and magnetic fields. Astrophys. J. 588, 1183–1198.CrossRefGoogle Scholar
14. Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
15. Ciliberto, S., Cioni, S. & Laroche, C. 1996 Large-scale flow properties of turbulent thermal convection. Phys. Rev. E 54, R5901–R5904.CrossRefGoogle ScholarPubMed
16. Ciliberto, S. & Laroche, C. 1999 Random roughness of boundary increases the turbulent convection scaling exponent. Phys. Rev. Lett. 82, 3998–4001.CrossRefGoogle Scholar
17. Cross, M. & Greenside, H. 2009 Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge University Press.CrossRefGoogle Scholar
18. Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851–1112.CrossRefGoogle Scholar
19. Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.CrossRefGoogle Scholar
20. Ginzburg, V. & Landau, L. 1950 On the theory of superconductivity. Zh. Eksp. Teor. Fiz. 20, 1064–1082.Google Scholar
21. Glatzmeier, G. A. & Roberts, P. H. 1995 A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 377, 203.CrossRefGoogle Scholar
22. Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle Scholar
23. Hébert, F., Hufschmid, R., Scheel, J. & Ahlers, G. 2010 Onset of Rayleigh–Bénard convection in cylindrical containers. Phys. Rev. E 81, 046318.CrossRefGoogle ScholarPubMed
24. Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.CrossRefGoogle Scholar
25. King, E., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. 2009 Boundary layer control of rotating convection systems. Nature 457, 301–304.CrossRefGoogle ScholarPubMed
26. Kunnen, R. 2008 Turbulent rotating convection. PhD thesis, University of Eindhoven.Google Scholar
27. Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008 Breakdown of large-scale circulation in turbulent rotating convection. Europhys. Lett. 84, 24001.CrossRefGoogle Scholar
28. Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2010 Experimental and numerical investigation of turbulent convection in a rotating cylinder. J. Fluid Mech. 642, 445–476.CrossRefGoogle Scholar
29. Liu, Y. & Ecke, R. 1997 Heat transport scaling in turbulent Rayleigh–Bénard convection: effects of rotation and Prandtl number. Phys. Rev. Lett. 79, 2257–2260.CrossRefGoogle Scholar
30. Liu, Y. & Ecke, R. 2009 Heat transport measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 80, 036314.CrossRefGoogle ScholarPubMed
31. Lohse, D. 2011Wind reversals in Rayleigh–Bénard convection. Talk During KITP Turbulence Conference,  http://online.kitp.ucsb.edu/online/turbulence11/lohse2/.Google Scholar
32. Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
33. Malkus, M. V. R. 1954a Discrete transitions in turbulent convection. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
34. Malkus, M. V. R. 1954b The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 185–195.Google Scholar
35. McWilliams, J. C. 1984 The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 146, 21–43.CrossRefGoogle Scholar
36. Nikolaenko, A., Brown, E., Funfschilling, D. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and less. J. Fluid Mech. 523, 251–260.CrossRefGoogle Scholar
37. Oresta, P., Stingano, G. & Verzicco, R. 2007 Transitional regimes and rotation effects in Rayleigh–Bénard convection in a slender cylindrical cell. Eur. J. Mech. B 26, 1–14.CrossRefGoogle Scholar
38. Qiu, X. L., Xia, K. Q. & Tong, P. 2005 Experimental study of velocity boundary layer near a rough conducting surface in turbulent natural convection. J. Turbul. 6, N30.CrossRefGoogle Scholar
39. Roche, P., Castaing, B., Chabaud, B., Hébral, B. & Sommeria, J. 2001a Side wall effects in Rayleigh–Bénard experiments. Eur. Phys. J. 24, 405–408.CrossRefGoogle Scholar
40. Roche, P. E., Castaing, B., Chabaud, B. & Hébral, B. 2001b Observation of the 1/2 power law in Rayleigh–Bénard convection. Phys. Rev. E 63, 045303.CrossRefGoogle Scholar
41. Rossby, H. T. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36, 309–335.CrossRefGoogle Scholar
42. Schlüter, A., Lortz, D. & Busse, F. H. 1965 On the stability of steady finite amplitude convection. J. Fluid Mech. 23, 129–144.CrossRefGoogle Scholar
43. Shen, Y., Tong, P. & Xia, K.-Q. 1996 Turbulent convection over rough surfaces. Phys. Rev. Lett. 76, 908–911.CrossRefGoogle ScholarPubMed
44. Sidorenkov, N. S. 2009 The Interaction Between Earth’s Rotation and Geophysical Processes. Wiley-VCH.CrossRefGoogle Scholar
45. Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
46. Stanley, H. 1971 Introduction to Phase Transitions and Critical Phenomena. Oxford Science Publications.Google Scholar
47. Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010 Optimal Prandtl number for heat transfer enhancement in rotating turbulent Rayleigh–Bénard convection. New J. Phys. 12, 075005.CrossRefGoogle Scholar
48. Stevens, R. J. A. M., Lohse, D. & Clercx, H. J. H. 2011aRotating Rayleigh–Bénard convection. Talk During KITP Turbulence Conference,  http://online.kitp.ucsb.edu/online/turbulence11/stevens/.Google Scholar
49. Stevens, R. J. A. M., Overkamp, J., Lohse, D. & Clercx, H. J. H. 2011b Effect of aspect-ratio on vortex distribution and heat transfer in rotating Rayleigh–Bénard convection. Phys. Rev. E (submitted).CrossRefGoogle ScholarPubMed
50. Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Ahlers, G. & Lohse, D. 2009 Transitions between turbulent states in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 024503.CrossRefGoogle ScholarPubMed
51. Sun, C., Ren, L.-Y., Song, H. & Xia, K.-Q. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells of widely varying aspect ratios. J. Fluid Mech. 542, 165–174.CrossRefGoogle Scholar
52. Tritton, D. J. 1988 Physical Fluid Dynamics. Oxford University Press.Google Scholar
53. Weiss, S. & Ahlers, G. 2011 Turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ration and Prandtl number Pr = 4.38. J. Fluid Mech. 676, 5–40.CrossRefGoogle Scholar
54. Weiss, S., Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Lohse, D. & Ahlers, G. 2010 Finite-size effects lead to supercritical bifurcations in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 105, 224501.CrossRefGoogle ScholarPubMed
55. Xi, H.-D. & Xia, K.-Q. 2008 Flow mode transition in turbulent thermal convection. Phys. Fluids 20, 055104.CrossRefGoogle Scholar
56. Xia, K.-Q. & Lui, S.-L. 1997 Turbulent thermal convection with an obstructed sidewall. Phys. Rev. Lett. 79, 5006–5009.CrossRefGoogle Scholar
57. Xu, X., Bajaj, K. M. S. & Ahlers, G. 2000 Heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 84, 4357–4360.CrossRefGoogle ScholarPubMed
58. Zhong, J.-Q. & Ahlers, G. 2010 Heat transport and the large-scale circulation in rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 665, 300–333.CrossRefGoogle Scholar
59. Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.Google ScholarPubMed
Supplementary material: PDF

Weiss and Ahlers supplementary material

Supplementary data tables

Download Weiss and Ahlers supplementary material(PDF)
PDF 56.9 KB