Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T00:55:19.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat transfer in a turbulent channel flow with square bars or circular rods on one wall

Published online by Cambridge University Press:  13 July 2015

S. Leonardi ,
P. Orlandi ,
L. Djenidi  and
R. A. Antonia
S. Leonardi*
Affiliation:
Department of Mechanical Engineering, The University of Texas at Dallas, Richardson, TX 75080, USA
P. Orlandi
Affiliation:
Dipartimento di Meccanica e Aeronautica, Università Degli Studi di Roma ‘La Sapienza’, 00184 Rome, Italy
L. Djenidi
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
R. A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

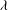Direct numerical simulations (DNS) are carried out to study the passive heat transport in a turbulent channel flow with either square bars or circular rods on one wall. Several values of the pitch (${\it\lambda}$) to height (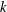$k$) ratio and two Reynolds numbers are considered. The roughness increases the heat transfer by inducing ejections at the leading edge of the roughness elements. The amounts of heat transfer and mixing depend on the separation between the roughness elements, an increase in heat transfer accompanying an increase in drag. The ratio of non-dimensional heat flux to the non-dimensional wall shear stress is higher for circular rods than square bars irrespectively of the pitch to height ratio. The turbulent heat flux varies within the cavities and is larger near the roughness elements. Both momentum and thermal eddy diffusivities increase relative to the smooth wall. For square cavities (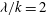${\it\lambda}/k=2$) the turbulent Prandtl number is smaller than for a smooth channel near the wall. As 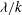${\it\lambda}/k$ increases, the turbulent Prandtl number increases up to a maximum of 2.5 at the crests plane of the square bars (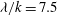${\it\lambda}/k=7.5$). With increasing distance from the wall, the differences with respect to the smooth wall vanish and at three roughness heights above the crests plane, the turbulent Prandtl number is essentially the same for smooth and rough walls.

JFM classification

Convection: Convection Flow Control: Mixing enhancement Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 512 - 530
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Antonia, R. A. & Kawamura, H. 2009 Correlation between small-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.CrossRefGoogle Scholar
Anderson, W., Barros, J. M., Christensen, K. T. & Awasthi, A. 2015 Numerical and experimental study of mechanisms responsible for turbulent secondary flows in boundary layer flows over spanwise heterogeneous roughness. J. Fluid Mech. 768, 316–347.CrossRefGoogle Scholar
Antonia, R. A., Abe, H. & Kawamura, H. 2009 Analogy between velocity and scalar fields in a turbulent channel flow. J. Fluid Mech. 628, 241–268.CrossRefGoogle Scholar
Antonia, R. A. & Kim, J. 1991 Turbulent Prandtl number in the near-wall region of a turbulent channel flow. Intl J. Heat Mass Transfer 34, 1905–1908.CrossRefGoogle Scholar
Coceal, O., Thomas, T. G., Castro, I. P. & Belcher, S. E. 2006 Mean flow and turbulence statistics over groups of urban-like cubical obstacles. Boundary-Layer Meteorol. 121, 491–519.Google Scholar
Djenidi, L., Elavarasan, R. & Antonia, R. A. 1999 The turbulent boundary layer over transverse square cavities. J. Fluid Mech. 395, 271–294.Google Scholar
Ekkad, S. V., Huang, Y. & Han, J.-C. 1998 Detailed heat transfer distributions in two-pass square channels with rib turbulators and bleed holes. Intl J. Heat Mass Transfer 41 (23), 3781–3791.Google Scholar
Grass, A. J., Stuart, R. J. & Mansour-Thehrani, M. 1993 Common vortical structure of turbulent flows over smooth and rough boundaries. AIAA J. 31, 837–846.CrossRefGoogle Scholar
Han, J. C., Dutta, S. & Ekkad, S. 2000 Gas Turbine Heat Transfer and Cooling Technology. Taylor and Francis.Google Scholar
Hetsroni, G., Mosyak, A., Rozenblit, R. & Yarin, L. P. 1999 Thermal patterns on the smooth and rough walls in turbulent flows. Intl J. Heat Mass Transfer 42, 3815–3829.Google Scholar
Hong, J., Katz, J. & Schultz, M. P. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.Google Scholar
Hussain, A. K. M. F. & Reynolds, W. C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41, 241–258.CrossRefGoogle Scholar
Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.CrossRefGoogle Scholar
Iritani, Y., Kasagi, N. & Hirota, M. 1983 Heat transfer mechanism and associated turbulence structure in the near-wall region of a turbulent boundary layer. In Turbulent Shear Flows (ed. Bradbury, L. J. S., Durst, F., Launder, B. E., Schmidt, F. W. & Whitelaw, J. H.), vol. 4, pp. 223–234. Springer.Google Scholar
Johansson, A. V. & Wikstrom, P. M. 1999 DNS and modeling of passive scalar transport in turbulent channel flow with focus on scalar dissipation modeling. Flow Turbul. Combust. 63, 223–245.Google Scholar
Kasagi, N., Tomita, Y. & Kuroda, A. 1992 Direct numerical simulation of passive scalar field in a turbulent channel flow. Trans. ASME 114, 598–606.Google Scholar
Kawamura, H., Abe, H. & Matsuo, Y. 1999 DNS of turbulent heat transfer in channel flow with respect to Reynolds and Prandtl number effect. Intl J. Heat Fluid Flow 20, 196–207.Google Scholar
Kawamura, H., Ohsaka, K. M., Abe, H. & Yamamoto, K. 1998 DNS of turbulent heat transfer in channel flow with low to medium–high Prandtl numbers fluid. Intl J. Heat Fluid Flow 19, 482–491.CrossRefGoogle Scholar
Kim, J. & Moin, P.1987 Transport of passive scalars in a turbulent channel flow. NASA Technical Memorandum TM-89463. NASA Ames Research Center, Moffat Field, California 94035.Google Scholar
Kim, J. & Moin, P. 1989 Transport of passive scalars in a turbulent channel flow. In Turbulent Shear Flows, vol. 6, pp. 85–96. Springer.Google Scholar
Krogstad, P.-A., Anderson, H. I., Bakken, O. M. & Ashrafian, A. 2005 An experimental and numerical study of channel flow with rough walls. J. Fluid Mech. 530, 327–352.Google Scholar
Krogstad, P. A. & Antonia, R. A. 1994 Structure of turbulent boundary layer on smooth and rough walls. J. Fluid Mech. 277, 1–21.Google Scholar
Leonardi, S. & Castro, I. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P., Djenidi, L. & Antonia, R. A. 2004 Structure of turbulent channel flow with square bars on one wall. Intl J. Heat Fluid Flow 25, 384–392.Google Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.CrossRefGoogle Scholar
Lu, S. S. & Willmarth, W. W. 1973 Measurements of the structure of Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–571.Google Scholar
Lyons, S. L., Hanratty, T. J. & McLaughlin, J. B. 1991 Direct numerical simulation of passive heat transfer in a turbulent channel flow. Intl J. Heat Mass Transfer 34, 1149–1161.Google Scholar
Mejia-Alvarez, R. & Christensen, K. T. 2010 Low-order representations of irregular surface roughness and their impact on a turbulent boundary layer. Phys. Fluids 22, 015106.CrossRefGoogle Scholar
Miyake, Y., Tsujimoto, K. & Nakaji, M. 2001 Direct numerical simulation of a rough–wall heat transfer in a turbulent channel flow. Intl J. Heat Fluid Flow 22, 237–244.Google Scholar
Nagano, Y., Hattori, H. & Houra, T. 2004 DNS of velocity and thermal fields in turbulent channel flow with transverse-rib roughness. Intl J. Heat Fluid Flow 25, 393–403.Google Scholar
Orlandi, P. 2000 Fluid Flow Phenomena, A Numerical Toolkit. Kluwer Academic.CrossRefGoogle Scholar
Orlandi, P. & Leonardi, S. 2006 DNS of turbulent channel flows with two- and three-dimensional roughness. J. Turbul. 7; doi:10.1080/14685240600827526.CrossRefGoogle Scholar
Perry, A. E. & Hoffmann, P. H. 1976 An experimental study of turbulent convective heat transfer from a flat plate. J. Fluid Mech. 77, 355–368.Google Scholar
Promvonge, P. & Thianpong, C. 2008 Thermal performance assessment of turbulent channel flows over different shaped ribs. Intl Commun. Heat Mass Transfer 35, 1327–1334.Google Scholar
Smalley, R. J., Leonardi, S., Antonia, R. A., Djenidi, L. & Orlandi, P. 2002 Reynolds stress anisotropy of turbulent rough wall layers. Exp. Fluids 33, 31–37.CrossRefGoogle Scholar
Tachie, M. F., Paul, S. S., Agelinchaa, M. & Shah, M. K. 2009 Structure of turbulent flow over 90 and 45 transverse ribs. J. Turbul. 10; doi:10.1080/14685240903045065.Google Scholar
Tanda, G. 2004 Heat transfer in rectangular channels with transverse and V-shaped broken ribs. Intl J. Heat Mass Transfer 47, 229–243.Google Scholar
Wang, L., Salewski, M. & Sundén, B. 2010 A turbulent flow in a ribbed channel: flow structures in the vicinity of a rib. Exp. Therm. Fluid Sci. 34, 165–176.Google Scholar
Won, S. Y. & Ligrani, P. M. 2004 Comparisons of flow structure and local Nusselt numbers in channels with parallel- and crossed-rib turbulators. Intl J. Heat Mass Transfer 47, 1573–1586.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.Google Scholar