Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T05:34:38.793Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth rate of a shocked mixing layer with known initial perturbations

Published online by Cambridge University Press:  14 May 2013

Christopher R. Weber ,
Andrew W. Cook  and
Riccardo Bonazza
Christopher R. Weber*
Affiliation:
University of Wisconsin, Madison, WI 53706, USA Lawrence Livermore National Laboratory, Livermore, CA 94551, USA
Andrew W. Cook
Affiliation:
Lawrence Livermore National Laboratory, Livermore, CA 94551, USA
Riccardo Bonazza
Affiliation:
University of Wisconsin, Madison, WI 53706, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive a growth-rate model for the Richtmyer–Meshkov mixing layer, given arbitrary but known initial conditions. The initial growth rate is determined by the net mass flux through the centre plane of the perturbed interface immediately after shock passage. The net mass flux is determined by the correlation between the post-shock density and streamwise velocity. The post-shock density field is computed from the known initial perturbations and the shock jump conditions. The streamwise velocity is computed via Biot–Savart integration of the vorticity field. The vorticity deposited by the shock is obtained from the baroclinic torque with an impulsive acceleration. 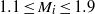Using the initial growth rate and characteristic perturbation wavelength as scaling factors, the model collapses the growth-rate curves and, in most cases, predicts the peak growth rate over a range of Mach numbers ($1. 1\leq {M}_{i} \leq 1. 9$), Atwood numbers (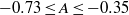$- 0. 73\leq A\leq - 0. 35$ and 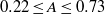$0. 22\leq A\leq 0. 73$), adiabatic indices (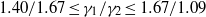$1. 40/ 1. 67\leq {\gamma }_{1} / {\gamma }_{2} \leq 1. 67/ 1. 09$) and narrow-band perturbation spectra. The mixing layer at late times exhibits a power-law growth with an average exponent of 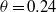$\theta = 0. 24$.

JFM classification

Mixing: Mixing Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 725 , 25 June 2013 , pp. 372 - 401
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, U., Hecht, J., Ofer, D. & Shvarts, D. 1995 Power laws and similarity of Rayleigh–Taylor and Richtmyer–Meshkov mixing fronts at all density ratios. Phys. Rev. Lett. 74 (4), 534–537.Google Scholar
Aschenbach, B., Egger, R. & Trömper, J 1995 Discovery of explosion fragments outside the Vela supernova remnant shock-wave boundary. Nature 373, 587–590.CrossRefGoogle Scholar
Barenblatt, G. I. 1983 Selfsimilar turbulence propagation from an instantaneous plane source. In Nonlinear Dynamics and Turbulence (ed. Barenblatt, G. I., Iooss, G. & Joseph, D. D.). pp. 48–60. Pitmann.Google Scholar
Barnes, C. W., Batha, S. H., Dunne, A. M., Magelssen, G. R., Rothman, S., Day, R. D., Elliott, N. E., Haynes, D. A., Holmes, R. L., Scott, J. M., Tubbs, D. L., Youngs, D. L., Boehly, T. R. & Jaanimagi, P. 2002 Observation of mix in a compressible plasma in a convergent cylindrical geometry. Phys. Plasmas 9 (11), 4431–4434.CrossRefGoogle Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.CrossRefGoogle Scholar
Cabot, W. H & Cook, A. W 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type ia supernovae. Nat. Phys. 2 (8), 562–568.CrossRefGoogle Scholar
Cook, A. W. 2007 Artificial fluid properties for large-eddy simulation of compressible turbulent mixing. Phys. Fluids 19, 055103.Google Scholar
Cook, A. W. 2009 Enthalpy diffusion in multicomponent flows. Phys. Fluids 21, 055109.Google Scholar
Cook, A. W., Cabot, W. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 333–362.CrossRefGoogle Scholar
Cook, A. W. & Cabot, W. H. 2005 Hyperviscosity for shock-turbulence interactions. J. Comput. Phys. 203, 379–385.CrossRefGoogle Scholar
Cook, A. W. & Dimotakis, P. E. 2001 Transition stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.CrossRefGoogle Scholar
Cotrell, D. L. & Cook, A. W. 2007 Scaling the incompressible Richtmyer–Meshkov instability. Phys. Fluids 19, 078105.Google Scholar
Dimonte, G. 2000 Spanwise homogeneous buoyancy-drag model for Rayleigh–Taylor mixing and experimental evaluation. Phys. Plasmas 7, 2255–2269.CrossRefGoogle Scholar
Dimonte, G. & Schneider, M. 1997 Turbulent Richtmyer–Meshkov instability experiments with strong radiatively driven shocks. Phys. Plasmas 4 (12), 4347–4357.CrossRefGoogle Scholar
Dimonte, G. & Schneider, M. 2000 Density ratio dependence of Rayleigh–Taylor mixing for sustained and impulsive acceleration histories. Phys. Fluids 12, 304–321.CrossRefGoogle Scholar
Fraley, G. 1986 Rayleigh–Taylor stability for a normal shock wave-density discontinuity interaction. Phys. Fluids 29 (2), 376–386.CrossRefGoogle Scholar
Goncharov, V. N. 2002 Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88 (13), 134502.CrossRefGoogle ScholarPubMed
Gowardhan, A. A., Ristorcelli, J. R. & Grinstein, F. F. 2011 The bipolar behaviour of the Richtmyer–Meshkov instability. Phys. Fluids 23 (7), 071701.Google Scholar
Griffond, J. 2006 Linear interaction analysis for Richtmyer–Meshkov instability at low Atwood numbers. Phys. Fluids 18 (5), 054106.CrossRefGoogle Scholar
Hahn, M., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2011 Richtmyer–Meshkov turbulent mixing arising from an inclined material interface with realistic surface perturbations and reshocked flow. Phys. Fluids 23 (4), 046101.CrossRefGoogle Scholar
Hecht, J., Alon, U. & Shvarts, D. 1994 Potential flow models of Rayleigh–Taylor and Richtmyer–Meshkov bubble fronts. Phys. Fluids 6, 4019–4030.CrossRefGoogle Scholar
Hillebrandt, W. & Niemeyer, J. C. 2000 Type ia supernova explosion models. Annu. Rev. Astron. Astrophys. 38 (1), 191–230.CrossRefGoogle Scholar
Jacobs, J. W. & Krivets, V. V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17 (3), 034105.CrossRefGoogle Scholar
Jacobs, J. W. & Sheeley, J. M. 1996 Experimental study of incompressible Richtmyer–Meshkov instability. Phys. Fluids 8 (2), 405–415.Google Scholar
Jun, B. I., Jones, T. W. & Norman, M. L 1996 Interaction of Rayleigh–Taylor fingers and circumstellar cloudlets in young supernova remnants. Astrophys. J. 468, L59–L63.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Elsevier.Google Scholar
Layzer, D. 1955 On the instability of superposed fluids in a gravitational field. Astrophys. J. 122, 1–12.CrossRefGoogle Scholar
Leinov, E., Malamud, G., Elbaz, Y., Levin, L. A, Ben-Dor, G., Shvarts, D. & Sadot, O. 2009 Experimental and numerical investigation of the Richtmyer–Meshkov instability under re-shock conditions. J. Fluid Mech. 626, 449–475.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Likhachev, O. A. & Jacobs, J. W. 2005 A vortex model for Richtmyer–Meshkov instability accounting for finite Atwood number. Phys. Fluids 17, 031704.CrossRefGoogle Scholar
Linden, P. F., Redondo, J. M. & Youngs, D. L. 1994 Molecular mixing in Rayleigh–Taylor instability. J. Fluid Mech. 265, 97–124.Google Scholar
Lindl, J. D., Amendt, P., Berger, R. L., Glendinning, S. G., Glenzer, S. H., Haan, S. W., Kauffman, R. L., Landen, O. L. & Suter, L. J. 2004 The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Phys. Plasmas 11 (2), 339–491.CrossRefGoogle Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2012 Transition to turbulence in shock-driven mixing: a Mach number study. J. Fluid Mech. 690, 203–266.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Izv. Akad. Nauk. SSSR Mekh. Zhidk. Gaza. 4, 151–157.Google Scholar
Meyer, K. A. & Blewett, P. J. 1972 Numerical investigation of the stability of a shock-accelerated interface between two fluids. Phys. Fluids 15 (5), 753–759.Google Scholar
Mikaelian, K. O. 1998 Analytic approach to nonlinear Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Phys. Rev. Lett. 80 (3), 508–511.CrossRefGoogle Scholar
Mikaelian, K. O. 2011 Extended model for Richtmyer–Meshkov mix. Physica D 240 (11), 935–942.Google Scholar
Motl, B., Oakley, J., Ranjan, D., Weber, C., Anderson, M. & Bonazza, R. 2009 Experimental validation of a Richtmyer–Meshkov scaling law over large density ratio and shock strength ranges. Phys. Fluids 21 (12), 126102.Google Scholar
Mueschke, N. J., Andrews, M. J. & Schilling, O. 2006 Experimental characterization of initial conditions and spatio-temporal evolution of a small-Atwood-number Rayleigh–Taylor mixing layer. J. Fluid Mech. 567, 27–63.CrossRefGoogle Scholar
Mueschke, N. J., Schilling, O., Youngs, D. L. & Andrews, M. J. 2009 Measurements of molecular mixing in a high-Schmidt-number Rayleigh–Taylor mixing layer. J. Fluid Mech. 632, 17–48.CrossRefGoogle Scholar
Poinsot, T. J. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101, 104–129.Google Scholar
Prasad, J. K., Rasheed, A., Kumar, S. & Sturtevant, B. 2000 The late-time development of the Richtmyer–Meshkov instability. Phys. Fluids 12 (8), 2108–2115.Google Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. London Math. Soc. 14, 170–177.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 23, 297–319.Google Scholar
Rikanati, A., Alon, U. & Shvarts, D. 1998 Vortex model for the nonlinear evolution of the multimode Richtmyer–Meshkov instability at low Atwood numbers. Phys. Rev. E 58 (6), 7410–7418.Google Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their plane. Proc. R. Soc. Lond. Ser. A 201, 192.Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, J. R. 2010 The influence of initial conditions on turbulent mixing due to Richtmyer–Meshkov instability. J. Fluid Mech. 654, 99–139.CrossRefGoogle Scholar
Vandenboomgaerde, M., Mügler, C. & Gauthier, S. 1998 Impulsive model for the Richtmyer–Meshkov instability. Phys. Rev. E 58 (2), 1874–1882.Google Scholar
Velikovich, A. L. 1996 Analytic theory of Richtmyer–Meshkov instability for the case of reflected rarefaction wave. Phys. Fluids 8 (6), 1666–1679.CrossRefGoogle Scholar
Velikovich, A. L. & Dimonte, G. 1996 Nonlinear perturbation theory of the incompressible Richtmyer–Meshkov instability. Phys. Rev. Lett. 76 (17), 3112–3115.CrossRefGoogle ScholarPubMed
Vetter, M. & Sturtevant, B. 1995 Experiments on the Richtmyer–Meshkov instability of an air/ F6 interface. Shock Waves 4, 247–252.CrossRefGoogle Scholar
Wouchuk, J. G. 2001a Growth rate of the linear Richtmyer–Meshkov instability when a shock is reflected. Phys. Rev. E 63 (5), 056303.Google Scholar
Wouchuk, J. G. 2001b Growth rate of the Richtmyer–Meshkov instability when a rarefaction is reflected. Phys. Plasmas 8 (6), 2890–2907.Google Scholar
Wouchuk, J. G. & Nishihara, K. 1996 Linear perturbation growth at a shocked interface. Phys. Plasmas 3 (10), 3761–3776.CrossRefGoogle Scholar
Wouchuk, J. G. & Nishihara, K. 1997 Asymptotic growth in the linear Richtmyer–Meshkov instability. Phys. Plasmas 4 (4), 1028–1038.Google Scholar
Wright, J. K. 1961 Shock Tubes. Methuen.Google Scholar
Yang, Y., Zhang, Q. & Sharp, D. H. 1994 Small amplitude theory of Richtmyer–Meshkov instability. Phys. Fluids 6 (5), 1856–1873.CrossRefGoogle Scholar
Zhang, Q. & Sohn, S. I. 1996 An analytical nonlinear theory of Richtmyer–Meshkov instability. Phys. Lett. A 212 (3), 149–155.Google Scholar
Youngs, D. L. 1994 Numerical simulation of mixing by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Laser Part. Beams 12, 725–750.Google Scholar
Zhang, Q. & Sohn, S. I. 1997 Nonlinear theory of unstable fluid mixing driven by shock wave. Phys. Fluids 9 (4), 1106–1124.CrossRefGoogle Scholar