Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-29T00:45:36.502Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth of multiparticle aggregates in sedimenting suspensions

Published online by Cambridge University Press:  24 February 2014

Alexander Z. Zinchenko  and
Robert H. Davis
Alexander Z. Zinchenko*
Affiliation:
Department of Chemical and Biological Engineering, University of Colorado, Boulder, CO 80309-0424, USA
Robert H. Davis
Affiliation:
Department of Chemical and Biological Engineering, University of Colorado, Boulder, CO 80309-0424, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The process of multiparticle aggregation in a dilute sedimenting suspension is rigorously simulated, with precise hydrodynamical interactions. The primary particles are monodisperse non-Brownian spheres at zero Reynolds number, with short-range molecular attractions. The rigid aggregates grow, as they settle downwards, by sequential particle addition – a valid assumption for dilute suspensions during the initial stages. The growth starts from doublet–particle interaction, but the indeterminate initial doublet concentration does not affect the results for cluster geometry and settling velocity. A new particle is generated far below a cluster with uniform probability density, and many trial particle–cluster relative trajectories are computed with high accuracy until a collision is found. The new cluster is then assumed to be rigid and allowed to reach a steady sedimentation regime (which is a spiral motion around the axis of steady rotation, ASR) before another particle is added, and so on. The ASR is typically far away from the cluster centre of mass. The Stokes flow solution algorithm for particle–cluster interaction works very efficiently with high-order multipoles (to order 100) and is extended to arbitrarily small particle–cluster separations by a geometry perturbation adapted from the conductivity simulations of Zinchenko (Phil. Trans. R. Soc. Lond. A, 1998, vol. 356, pp. 2953–2998). Clusters are generated to 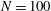$N=100$ spheres, with extensive averaging over many growth realizations. The fractal scaling 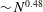$\sim N^{0.48}$ for the cluster settling speed is quickly attained once 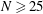$N\geq 25$, and the exponent 0.48 is practically independent of the strength of molecular forces. The cluster fractal dimension is predicted to be 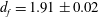$d_f=1.91\pm 0.02$ (in contrast to the existing views that sequential addition can only produce high-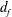$d_f$ clusters). Several average characteristics of the cluster size are also computed. The theoretical settling speed has no adjustable parameters and agrees reasonably well with prior experiments for a moderately polydisperse system in a broad range of cluster sizes.

JFM classification

Complex Fluids: Suspensions Multiphase and Particle-laden Flows: Particle/fluid flow Nonlinear Dynamical Systems: Fractals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 742 , 10 March 2014 , pp. 577 - 617
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1972 Sedimentation in a dilute dispersion of spheres. J. Fluid Mech. 52, 245–268.CrossRefGoogle Scholar
Batchelor, G. K. & Green, J. T. 1972 The determination of the bulk stress in a suspension of spherical particles to order $c^2$ . J. Fluid Mech. 56, 401–427.CrossRefGoogle Scholar
Binder, C., Feichtinger, C., Schmid, H.-J., Thürey, N., Peukert, W. & Rüde, U. 2006 Simulation of the hydrodynamic drag of aggregated particles. J. Colloid Interface Sci. 301, 155–167.CrossRefGoogle ScholarPubMed
Binder, C., Hartig, M. A. J. & Peukert, W. 2009 Structural dependent drag force and orientation prediction for small fractal aggregates. J. Colloid Interface Sci. 331, 243–250.CrossRefGoogle ScholarPubMed
Cichocki, B., Felderhof, B. U. & Schmitz, R. 1988 Hydrodynamic interactions between two spherical particles. Physico-Chem. Hydrodyn. 10, 383–403.Google Scholar
Chopard, B., Nguyen, H. & Stoll, S. 2006 A lattice Boltzmann study of the hydrodynamic properties of 3D fractal aggregates. Maths Comput. Simul. 72, 103–107.CrossRefGoogle Scholar
Cooley, M. D. A. & O’Neill, M. E. 1969 On the slow motion generated in a viscous fluid by the approach of a sphere to a plane wall or stationary sphere. Mathematika 16, 37–49.CrossRefGoogle Scholar
Cox, R. G. & Brenner, H. 1971 The rheology of a suspension of particles in a Newtonian fluid. Chem. Eng. Sci. 26, 65–93.CrossRefGoogle Scholar
Durlofsky, L., Brady, J. F. & Bossis, G. 1987 Dynamic simulation of hydrodynamically interacting particles. J. Fluid Mech. 180, 21–49.CrossRefGoogle Scholar
Ehrl, L., Soos, M. & Lattuada, M. 2009 Generation and geometrical analysis of dense clusters with variable fractal dimension. J. Phys. Chem. B 113, 10587–10599.CrossRefGoogle ScholarPubMed
Filippov, A. V. 2000 Drag and torque on clusters of $N$ arbitrary spheres at low Reynolds number. J. Colloid Interface Sci. 229, 184–195.CrossRefGoogle Scholar
Guckel, E. K.1999 Large scale simulations of particulate systems using the PME method. PhD thesis, University of Illinois, Urbana-Champaign.Google Scholar
Happel, J. & Brenner, H. 1973 Low Reynolds Number Hydrodynanmics. Nijhoff.Google Scholar
Harshe, Y. M., Ehrl, L. & Lattuada, M. 2010 Hydrodynamic properties of rigid fractal aggregates of arbitrary morphology. J. Colloid Interface Sci. 352, 87–98.CrossRefGoogle ScholarPubMed
Huang, H. 1994 Fractal properties of flocs formed by fluid shear and differential settling. Phys. Fluids 6, 3229–3234.CrossRefGoogle Scholar
Ingber, M. S., Feng, S., Graham, A. L. & Brenner, H. 2008 The analysis of self-diffusion and migration of rough spheres in nonlinear shear flow using a traction-corrected boundary element method. J. Fluid Mech. 598, 267–292.CrossRefGoogle Scholar
Jiang, Q. & Logan, B. E. 1991 Fractal dimensions of aggregates determined from steady-state size distributions. Environ. Sci. Technol. 25, 2031–2038.CrossRefGoogle Scholar
Jullien, R., Botet, R. & Mors, P. M. 1987 Computer simulation of cluster–cluster aggregation. Faraday Discuss. Chem. Soc. 83, 125–137.CrossRefGoogle Scholar
Kumar, A. & Higdon, J. J. L. 2011 Particle mesh Ewald Stokesian dynamics simulations for suspensions of nonspherical particles. J. Fluid Mech. 675, 297–335.CrossRefGoogle Scholar
Lattuada, M., Wu, H. & Morbidelli, M. 2003 A simple model for the structure of fractal aggregates. J. Colloid Interface Sci. 268, 106–120.CrossRefGoogle ScholarPubMed
Logan, B. E. & Kilps, J. R. 1995 Fractal dimensions of aggregates formed in different fluid mechanical environments. Water Res. 29, 443–453.CrossRefGoogle Scholar
Logan, B. E. & Wilkinson, D. B. 1990 Fractal geometry of marine snow and other biological aggregates. Limnol. Oceanogr. 35, 130–136.CrossRefGoogle Scholar
Meakin, P. 1984 Effect of cluster trajectories on cluster–cluster aggregation: a comparison of linear and Brownian trajectories in two- and three-dimensional simulations. Phys. Rev. A 29, 997–999.CrossRefGoogle Scholar
Meakin, P. 1985 Accretion processes with linear particle trajectories. J. Colloid Interface Sci. 105, 240–246.CrossRefGoogle Scholar
Meakin, P. & Family, F. 1987 Structure and dynamics of reaction-limited aggregation. Phys. Rev. A 36, 5498–5501.CrossRefGoogle ScholarPubMed
Meng, Q. & Higdon, J. J. L. 2008 Large scale dynamic simulation of plate-like particle suspensions. Part I: Non-Brownian simulation. J. Rheol. 52, 1–36.CrossRefGoogle Scholar
Mo, G. & Sangani, A. S. 1994 A method for computing Stokes flow interactions among spherical objects and its application to suspensions of drops and porous particles. Phys. Fluids 6, 1637–1652.CrossRefGoogle Scholar
O’Neill, M. E. & Majumdar, S. R. 1970 Asymmetrical slow viscous fluid motions caused by the translation or rotation of two spheres. Part II: Asymptotic forms of the solutions when the minimum clearance between the spheres approaches zero. Z. Angew. Math. Phys. 21, 180–189.CrossRefGoogle Scholar
Power, H. & Miranda, G. 1987 Second kind integral equation formulation of Stokes flow past a particle of arbitrary shape. SIAM J. Appl. Maths 47, 689–698.CrossRefGoogle Scholar
Sangani, A. S. & Acrivos, A. 1982 Slow flow through a periodic array of spheres. Int. J. Multiphase Flow 8, 343–360.CrossRefGoogle Scholar
Sangani, A. S. & Mo, G. 1994 Inclusion of lubrication forces in dynamic simulations. Phys. Fluids 6, 1653–1662.CrossRefGoogle Scholar
Schaefer, D. W. 1989 Polymers, fractals and ceramic materials. Science 243, 1023–1027.CrossRefGoogle ScholarPubMed
Schmitz, R. & Felderhof, B. U. 1982 Creeping flow about a spherical particle. Physica 113A, 90–102.CrossRefGoogle Scholar
Sierou, A. & Brady, J. F. 2001 Accelerated Stokesian dynamics simulations. J. Fluid Mech. 448, 115–146.CrossRefGoogle Scholar
Sutherland, D. N. 1966 Comments on Vold’s simulation of floc formation. J. Colloid Interface Sci. 22, 300–302.CrossRefGoogle Scholar
Thouy, R. & Jullien, R. 1996 Structure factors for fractal aggregates built off-lattice with tunable fractal dimension. J. Phys. I (Paris) 6, 1365–1376.Google Scholar
Torres, F. E., Russel, W. B. & Schowalter, W. R. 1991a Floc structure and growth kinetics for rapid shear coagulation of polystyrene colloids. J. Colloid Interface Sci. 142, 554–574.CrossRefGoogle Scholar
Torres, F. E., Russel, W. B. & Schowalter, W. R. 1991b Simulations of coagulation in viscous flows. J. Colloid Interface Sci. 145, 51–73.CrossRefGoogle Scholar
Vanni, M. 2000 Creeping flow over spherical permeable aggregates. Chem. Engng Sci. 55, 685–698.CrossRefGoogle Scholar
Verwey, E. J. W. & Overbeek, J. Th. G. 1948 Theory of the Stability of Lyophobic Colloids. Elsevier.Google Scholar
Zinchenko, A. Z. 1994 An efficient algorithm for calculating multiparticle thermal interaction in a concentrated dispersion of spheres. J. Comput. Phys. 111, 120–135.CrossRefGoogle Scholar
Zinchenko, A. Z. 1998 Effective conductivity of loaded granular materials by numerical simulation. Phil. Trans. R. Soc. Lond. A 356, 2953–2998.CrossRefGoogle Scholar
Zinchenko, A. Z. & Davis, R. H. 2000 An efficient algorithm for hydrodynamical interaction of many deformable drops. J. Comput. Phys. 157, 539–587.CrossRefGoogle Scholar
Zinchenko, A. Z. & Davis, R. H. 2002 Shear flow of highly concentrated emulsions of deformable drops by numerical simulations. J. Fluid Mech. 455, 21–62.CrossRefGoogle Scholar
Zinchenko, A. Z. & Davis, R. H. 2008 Algorithm for direct numerical simulation of emulsion flow through a granular material. J. Comput. Phys. 227, 7841–7888.CrossRefGoogle Scholar
Zinchenko, A. Z. & Davis, R. H. 2013 Emulsion flow through a packed bed with multiple drop breakup. J. Fluid Mech. 725, 611–663.CrossRefGoogle Scholar
Zinchenko, A. Z., Rother, M. A. & Davis, R. H. 2011 Gravity-induced collisions of spherical drops covered with compressible surfactant. J. Fluid Mech. 667, 369–402.CrossRefGoogle Scholar