Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T17:57:31.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Granular segregation in circular tumblers: theoretical model and scaling laws

Published online by Cambridge University Press:  28 January 2015

Conor P. Schlick ,
Yi Fan ,
Paul B. Umbanhowar ,
Julio M. Ottino  and
Richard M. Lueptow
Conor P. Schlick
Affiliation:
Department of Engineering Sciences and Applied Mathematics, Northwestern University, Evanston, IL 60208, USA
Yi Fan
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, IL 60208, USA The Dow Chemical Company, Midland, MI 48667, USA
Paul B. Umbanhowar
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, IL 60208, USA
Julio M. Ottino
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, IL 60208, USA Department of Chemical and Biological Engineering, Northwestern University, Evanston, IL 60208, USA The Northwestern University Institute on Complex Systems (NICO), Northwestern University, Evanston, IL 60208, USA
Richard M. Lueptow*
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, IL 60208, USA The Northwestern University Institute on Complex Systems (NICO), Northwestern University, Evanston, IL 60208, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

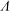We model bidisperse size segregation of granular material in quasi-two-dimensional circular tumbler flow using the advection–diffusion transport equation with an additional term to account for segregation due to percolation. Segregation depends on three dimensionless parameters: the ratio of segregation to advection, ${\it\Lambda}$; the ratio of advection to diffusion, 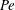$\mathit{Pe}$; and the dimensionless flowing layer depth, ${\it\epsilon}$. The degree of segregation in steady state depends only on the ratio of segregation effects to diffusion effects, 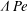${\it\Lambda}\,\mathit{Pe}$, and the degree of segregation increases as 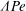${\it\Lambda}\mathit{Pe}$ increases. 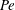The transient time to reach steady-state segregation depends only on advection, which is manifested in ${\it\epsilon}$ and $\mathit{Pe}$ when 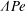${\it\Lambda}\mathit{Pe}$ is constant. This model is also applied to unsteady tumbler flow, where the rotation speed varies with time.

JFM classification

Complex Fluids: Complex Fluids Granular media: Granular media Mixing: Granular mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 632 - 652
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexander, A., Shinbrot, T. & Muzzio, F. J. 2002 Scaling surface velocities in rotating cylinders as a function of vessel radius, rotation rate, and particle size. Powder Technol. 126 (2), 174–190.Google Scholar
Alizadeh, E., Bertrand, F. & Chaouki, J. 2014 Comparison of DEM results and Lagrangian experimental data for the flow and mixing of granules in a rotating drum. AIChE J. 60 (1), 60–75.CrossRefGoogle Scholar
Arntz, M. M. H. D., Beeftink, H. H., den Otter, W. K., Briels, W. J. & Boom, R. M. 2014 Segregation of granular particles by mass, radius, and density in a horizontal rotating drum. AIChE J. 60 (1), 50–59.Google Scholar
Bonamy, D., Daviaud, F. & Laurent, L. 2002 Experimental study of granular surface flows via a fast camera: a continuous description. Phys. Fluids 14 (5), 1666–1673.CrossRefGoogle Scholar
Boutreux, T. 1998 Surface flows of granular mixtures: II. Segregation with grains of different size. Eur. Phys. J. B 6 (3), 419–424.Google Scholar
Bridgwater, J., Foo, W. S. & Stephens, D. J. 1985 Particle mixing and segregation in failure zones – theory and experiment. Powder Technol. 41 (2), 147–158.Google Scholar
Cantelaube, F. & Bideau, D. 1995 Radial segregation in a 2D drum: an experimental analysis. Europhys. Lett. 30 (3), 133–138.Google Scholar
Chakraborty, S., Nott, P. R. & Prakash, J. R. 2000 Analysis of radial segregation of granular mixtures in a rotating drum. Eur. Phys. J. E 1 (4), 265–273.Google Scholar
Christov, I. C., Ottino, J. M. & Lueptow, R. M. 2010 Chaotic mixing via streamline jumping in quasi-two-dimensional tumbled granular flows. Chaos 20, 023102.Google Scholar
Christov, I. C., Ottino, J. M. & Lueptow, R. M. 2011 From streamline jumping to strange eigenmodes: bridging the Lagrangian and Eulerian pictures of the kinematics of mixing in granular flows. Phys. Fluids 23 (10), 103302.Google Scholar
Cisar, S. E., Umbanhowar, P. B. & Ottino, J. M. 2006 Radial granular segregation under chaotic flow in two-dimensional tumblers. Phys. Rev. E 74, 051305.Google Scholar
Danckwerts, P. V. 1952 The definition and measurement of some characteristics of mixtures. Appl. Sci. Res. A 3 (4), 279–296.CrossRefGoogle Scholar
Dolgunin, V. N. & Ukolov, A. A. 1995 Segregation modeling of particle rapid gravity flow. Powder Technol. 83 (2), 95–103.Google Scholar
Drahun, J. A. & Bridgwater, J. 1983 The mechanisms of free surface segregation. Powder Technol. 36, 39–53.CrossRefGoogle Scholar
Dury, C. M. & Ristow, G. H. 1997 Radial segregation in a two-dimensional rotating drum. J. Phys. (Paris) I 7 (5), 737–745.Google Scholar
Dury, C. M. & Ristow, G. H. 1999 Competition of mixing and segregation in rotating cylinders. Phys. Fluids 11 (6), 1387–1394.Google Scholar
Fan, Y. & Hill, K. M. 2011 Theory for shear-induced segregation of dense granular mixtures. New J. Phys. 13, 095009.Google Scholar
Fan, Y., Schlick, C. P., Umbanhowar, P. B., Ottino, J. M. & Lueptow, R. M. 2014a Modelling size segregation of granular materials: the roles of segregation, advection and diffusion. J. Fluid Mech. 741, 252–279.Google Scholar
Fan, Y., Umbanhowar, P. B., Ottino, J. M. & Lueptow, R. M. 2013 Kinematics of monodisperse and bidisperse granular flows in quasi-two-dimensional bounded heaps. Proc. R. Soc. Lond. A 469, 20130235.Google Scholar
Fan, Y., Umbanhowar, P. B., Ottino, J. M. & Lueptow, R. M. 2015 Collisional diffusion in rapid and creep flow regimes for granular materials. Phys. Rev. E (under review).Google Scholar
Fiedor, S. J. & Ottino, J. M. 2005 Mixing and segregation of granular matter: multi-lobe formation in time-periodic flows. J. Fluid Mech. 533, 223–236.CrossRefGoogle Scholar
Gray, J. M. N. T. & Ancey, C. 2009 Segregation, recirculation and deposition of coarse particles near two-dimensional avalanche fronts. J. Fluid Mech. 629, 387–423.CrossRefGoogle Scholar
Gray, J. M. N. T. & Ancey, C. 2011 Multi-component particle-size segregation in shallow granular avalanches. J. Fluid Mech. 678, 535–588.Google Scholar
Gray, J. M. N. T. & Chugunov, V. A. 2006 Particle-size segregation and diffusive remixing in shallow granular avalanches. J. Fluid Mech. 569, 365–398.Google Scholar
Gray, J. M. N. T. & Hutter, K. 1997 Pattern formation in granular avalanches. Contin. Mech. Thermodyn. 9 (6), 341–345.Google Scholar
Gray, J. M. N. T., Shearer, M. & Thornton, A. R. 2006 Time-dependent solutions for particle-size segregation in shallow granular avalanches. Proc. R. Soc. Lond. A 462 (2067), 947–972.Google Scholar
Gray, J. M. N. T. & Thornton, A. R. 2005 A theory for particle size segregation in shallow granular free-surface flows. Proc. R. Soc. Lond. A 461, 1447–1473.Google Scholar
Hill, K. M., Gioia, G. & Amaravadi, D. 2004 Radial segregation patterns in rotating granular mixtures: waviness selection. Phys. Rev. Lett. 93, 224301.Google Scholar
Hill, K. M., Khakhar, D. V., Gilchrist, J. F., McCarthy, J. J. & Ottino, J. M. 1999 Segregation-driven organization in chaotic granular flows. Proc. Natl Acad. Sci. USA 96, 11701–11706.Google Scholar
Hutter, K., Svendsen, B. & Rickenmann, D. 1996 Debris flow modeling: a review. Contin. Mech. Thermodyn. 8 (1), 1–35.Google Scholar
Jain, N., Ottino, J. M. & Lueptow, R. M. 2002 An experimental study of the flowing granular layer in a rotating tumbler. Phys. Fluids 14 (2), 572–582.Google Scholar
Jain, N., Ottino, J. M. & Lueptow, R. M. 2004 Effect of interstitial fluid on a granular flowing layer. J. Fluid Mech. 508, 23–44.Google Scholar
Jain, N., Ottino, J. M. & Lueptow, R. M. 2005 Regimes of segregation and mixing in combined size and density granular systems: an experimental study. Granul. Matt. 7 (2–3), 69–81.CrossRefGoogle Scholar
Khakhar, D. V., Orpe, A. V. & Ottino, J. M. 2001 Continuum model of mixing and size segregation in a rotating cylinder: concentration–flow coupling and streak formation. Powder Technol. 116 (2–3), 232–245.Google Scholar
Makse, H. A. 1999 Continuous avalanche segregation of granular mixtures in thin rotating drums. Phys. Rev. Lett. 83 (16), 3186–3189.Google Scholar
Marks, B., Rognon, P. & Einav, I. 2012 Grainsize dynamics of polydisperse granular segregation down inclined planes. J. Fluid Mech. 690, 499–511.Google Scholar
May, L. B. H., Golick, L. A., Phillips, K. C., Shearer, M. & Daniels, K. E. 2010 Shear-driven size segregation of granular materials: modeling and experiment. Phys. Rev. E 81, 051301.Google Scholar
Meier, S. W., Barreiro, D. A. M., Ottino, J. M. & Lueptow, R. M. 2008 Coarsening of granular segregation patterns in quasi-two-dimensional tumblers. Nat. Phys. 4 (3), 244–248.Google Scholar
Meier, S. W., Cisar, S. E., Lueptow, R. M. & Ottino, J. M. 2006 Capturing patterns and symmetries in chaotic granular flow. Phys. Rev. E 74, 031310.Google Scholar
Meier, S. W., Lueptow, R. M. & Ottino, J. M. 2007 A dynamical systems approach to mixing and segregation of granular materials in tumblers. Adv. Phys. 56 (5), 757–827.Google Scholar
Mellmann, J. 2001 The transverse motion of solids in rotating cylinders – forms of motion and transition behavior. Powder Technol. 118 (3), 251–270.Google Scholar
Metcalfe, G. 1996 Experiments on mixing and segregating granular materials. In Chemeca 96: Excellence in Chemical Engineering, 24th Australian and New Zealand Chemical Engineering Conference and Exhibition, vol. 6, pp. 123–128. Institution of Engineers.Google Scholar
Orpe, A. V. & Khakhar, D. V. 2001 Scaling relations for granular flow in quasi-two-dimensional rotating cylinders. Phys. Rev. E 64, 031302.Google Scholar
Ottino, J. M. & Khakhar, D. V. 2000 Mixing and segregation of granular materials. Annu. Rev. Fluid Mech. 32, 55–91.Google Scholar
Pereira, G. G. & Cleary, P. W. 2013 Radial segregation of multi-component granular media in a rotating tumbler. Granul. Matt. 15 (6), 705–724.Google Scholar
Pignatel, F., Asselin, C., Krieger, L., Christov, I. C., Ottino, J. M. & Lueptow, R. M. 2012 Parameters and scalings for dry and immersed granular flowing layers in rotating tumblers. Phys. Rev. E 86, 011304.Google Scholar
Prigozhin, L. & Kalman, H. 1998 Radial mixing and segregation of a binary mixture in a rotating drum: model and experiment. Phys. Rev. E 57 (2), 2073–2080.Google Scholar
Savage, S. B. & Lun, C. K. K. 1988 Particle size segregation in inclined chute flow of dry cohesionless granular solids. J. Fluid Mech. 189, 311–335.Google Scholar
Schlick, C. P., Christov, I. C., Umbanhowar, P. B., Ottino, J. M. & Lueptow, R. M. 2013 A mapping method for distributive mixing with diffusion: interplay between chaos and diffusion in time-periodic sine flow. Phys. Fluids 25 (5), 052102.Google Scholar
Schlick, C. P., Fan, Y., Isner, A. B., Umbanhowar, P. B., Ottino, J. M. & Lueptow, R. M. 2015 Modeling segregation of bidisperse granular materials using physical control parameters in the quasi-2D bounded heap. AIChE J. (in revision).Google Scholar
Shearer, M., Gray, J. M. N. T. & Thornton, A. R. 2008 Stable solutions of a scalar conservation law for particle-size segregation in dense granular avalanches. Eur. J. Appl. Maths 19 (1), 61–86.Google Scholar
Shinohara, K., Shoji, K. & Tanaka, T. 1972 Mechanism of size segregation of particles in filling a hopper. Ind. Engng Chem. Process. Des. Dev. 11, 369–376.Google Scholar
Silbert, L. E., Grest, G. S., Brewster, R. & Levine, A. J. 2007 Rheology and contact lifetimes in dense granular flows. Phys. Rev. Lett. 99, 068002.CrossRefGoogle ScholarPubMed
Singh, M. K., Galaktionov, O. S., Meijer, H. E. H. & Anderson, P. D. 2009 A simplified approach to compute distribution matrices for the mapping method. Comput. Chem. Engng 33 (8), 1354–1362.Google Scholar
Thornton, A. R. & Gray, J. M. N. T. 2008 Breaking size segregation waves and particle recirculation in granular avalanches. J. Fluid Mech. 596, 261–284.Google Scholar
Tunuguntla, D. R., Bokhove, O. & Thornton, A. R. 2014 A mixture theory for size and density segregation in shallow granular free-surface flows. J. Fluid Mech. 749, 99–112.Google Scholar
Williams, J. C. 1968 The mixing of dry powders. Powder Technol. 2, 13–20.Google Scholar
Woodhouse, M. J., Thornton, A. R., Johnson, C. G., Kokelaar, B. P. & Gray, J. M. N. T. 2012 Segregation-induced fingering instabilities in granular free-surface flows. J. Fluid Mech. 709, 543–580.Google Scholar

Schlick et al. supplementary movie

A movie of the theoretical prediction of a rotating tumbler with ε=0.1, Λ=1.5, and Pe=30 over 1.5 rotations.

Download Schlick et al. supplementary movie(Video)
Video 3 MB

Schlick et al. supplementary movie

A movie of the theoretical prediction of a rotating tumbler with ε=0.1, Λ=1.5, and Pe=30 over 1.5 rotations.

Download Schlick et al. supplementary movie(Video)
Video 1.6 MB