Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Guevel, Y.
Girault, G.
and
Cadou, J.M.
2014.
Parametric analysis of steady bifurcations in 2D incompressible viscous flow with high order algorithm.
Computers & Fluids,
Vol. 100,
Issue. ,
p.
185.
Lashgari, Iman
Tammisola, Outi
Citro, Vincenzo
Juniper, Matthew P.
and
Brandt, Luca
2014.
The planar X-junction flow: stability analysis and control.
Journal of Fluid Mechanics,
Vol. 753,
Issue. ,
p.
1.
Jotkar, Mamta
Pérez, José Miguel
Theofilis, Vassilis
and
Govindarajan, Rama
2015.
Instability and Control of Massively Separated Flows.
Vol. 107,
Issue. ,
p.
177.
Si, Xinhui
Pan, Mingyang
Zheng, Liancun
Zhou, Jianhui
and
Li, Lin
2016.
The solutions for the flow of micropolar fluid through an expanding or contracting channel with porous walls.
Boundary Value Problems,
Vol. 2016,
Issue. 1,
Wahba, E. M.
2016.
A pressure-based velocity decomposition procedure for the incompressible Navier–Stokes equations.
Meccanica,
Vol. 51,
Issue. 8,
p.
1675.
Jotkar, Mamta R.
Swaminathan, Gayathri
Sahu, Kirti Chandra
and
Govindarajan, Rama
2016.
Global Linear Instability of Flow Through a Converging–Diverging Channel.
Journal of Fluids Engineering,
Vol. 138,
Issue. 3,
Quaini, A.
Glowinski, R.
and
Čanić, S.
2016.
Symmetry breaking and preliminary results about a Hopf bifurcation for incompressible viscous flow in an expansion channel.
International Journal of Computational Fluid Dynamics,
Vol. 30,
Issue. 1,
p.
7.
Praveen, T.
and
Eswaran, V.
2017.
Transition to asymmetric flow in a symmetric sudden expansion: Hydrodynamics and MHD cases.
Computers & Fluids,
Vol. 148,
Issue. ,
p.
103.
Carling, Paul
Williams, Jon
Leyland, Julian
and
Esteves, Luciana
2018.
Storm-wave development of shore-normal grooves (gutters) on a steep sandstone beach face.
Estuarine, Coastal and Shelf Science,
Vol. 207,
Issue. ,
p.
312.
Chu, Xu
Wu, Yongxiang
Rist, Ulrich
and
Weigand, Bernhard
2020.
Instability and transition in an elementary porous medium.
Physical Review Fluids,
Vol. 5,
Issue. 4,
Wu, Yongxiang
Römer, Tristan
Axtmann, Gabriel
and
Rist, Ulrich
2022.
Transition mechanisms in a boundary layer controlled by rotating wall-normal cylindrical roughness elements.
Journal of Fluid Mechanics,
Vol. 945,
Issue. ,
Frantz, R. A. S.
Loiseau, J.-Ch.
and
Robinet, J.-Ch.
2023.
Krylov Methods for Large-Scale Dynamical Systems: Application in Fluid Dynamics.
Applied Mechanics Reviews,
Vol. 75,
Issue. 3,
Liu, Wentao
Wang, Zhichao
Zhao, Hui
Li, Weifeng
and
Liu, Haifeng
2024.
Characteristics of gel entrainment induced by gas recirculation in coaxial gas–liquid jets.
Physics of Fluids,
Vol. 36,
Issue. 7,
Yu, Kaikai
Hao, Jiaao
Wen, Chih-Yung
and
Xu, Jinglei
2024.
Bi-global stability of supersonic backward-facing step flow.
Journal of Fluid Mechanics,
Vol. 981,
Issue. ,
Ducimetière, Yves-Marie
Boujo, Edouard
and
Gallaire, François
2024.
Noise-induced transitions past the onset of a steady symmetry-breaking bifurcation: The case of the sudden expansion.
Physical Review Fluids,
Vol. 9,
Issue. 5,
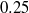 to
to 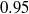 . By means of a three-dimensional linear stability analysis global temporal modes are scrutinized. In a symmetric expansion the primary bifurcation is stationary and two-dimensional, breaking the mirror symmetry with respect to the mid-plane. The secondary asymmetric flow experiences a secondary instability to different three-dimensional modes, depending on the expansion ratio. For a moderately asymmetric expansion only one of the two secondary flows (the connected branch) is realized at low Reynolds numbers. Since the perturbed secondary flow does not deviate much from the symmetric secondary flow, both secondary stability boundaries are very close to each other. For very small and very large expansion ratios an asymptotic behaviour is found for suitably scaled critical Reynolds numbers and wavenumbers. Representative instabilities are analysed in detail using an a posteriori energy transfer analysis to reveal the physical nature of the instabilities. Depending on the geometry, pure centrifugal and elliptical amplification processes are identified. We also find that the basic flow can become unstable due to the effects of flow deceleration, streamline convergence and high shear stresses, respectively.
. By means of a three-dimensional linear stability analysis global temporal modes are scrutinized. In a symmetric expansion the primary bifurcation is stationary and two-dimensional, breaking the mirror symmetry with respect to the mid-plane. The secondary asymmetric flow experiences a secondary instability to different three-dimensional modes, depending on the expansion ratio. For a moderately asymmetric expansion only one of the two secondary flows (the connected branch) is realized at low Reynolds numbers. Since the perturbed secondary flow does not deviate much from the symmetric secondary flow, both secondary stability boundaries are very close to each other. For very small and very large expansion ratios an asymptotic behaviour is found for suitably scaled critical Reynolds numbers and wavenumbers. Representative instabilities are analysed in detail using an a posteriori energy transfer analysis to reveal the physical nature of the instabilities. Depending on the geometry, pure centrifugal and elliptical amplification processes are identified. We also find that the basic flow can become unstable due to the effects of flow deceleration, streamline convergence and high shear stresses, respectively.