Hostname: page-component-5f56664f6-2gss9 Total loading time: 0 Render date: 2025-05-08T00:32:04.549Z Has data issue: false hasContentIssue false
  • English
  • Français

Global modes and nonlinear analysis of inverted-flag flapping

Published online by Cambridge University Press:  22 October 2018

Andres Goza Open the ORCID record for Andres Goza [Opens in a new window] ,
Tim Colonius  and
John E. Sader Open the ORCID record for John E. Sader [Opens in a new window]
Andres Goza*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08540, USA
Tim Colonius
Affiliation:
Department of Mechanical and Civil Engineering, California Institute of Technology, Pasadena, CA 91125, USA
John E. Sader
Affiliation:
ARC Centre of Excellence in Exciton Science, School of Mathematics and Statistics, University of Melbourne, Victoria 3010, Australia Department of Physics, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An inverted flag has its trailing edge clamped and exhibits dynamics distinct from that of a conventional flag, whose leading edge is restrained. We perform nonlinear simulations and a global stability analysis of the inverted-flag system for a range of Reynolds numbers, flag masses and stiffnesses. Our global stability analysis is based on a linearisation of the fully coupled fluid–structure system of equations. The calculated equilibria are steady-state solutions of the fully coupled nonlinear equations. By implementing this approach, we (i) explore the mechanisms that initiate flapping, (ii) study the role of vorticity generation and vortex-induced vibration (VIV) in large-amplitude flapping and (iii) characterise the chaotic flapping regime. For point (i), we identify a deformed-equilibrium state and show through a global stability analysis that the onset of small-deflection flapping – where the oscillation amplitude is significantly smaller than in large-amplitude flapping – is due to a supercritical Hopf bifurcation. For large-amplitude flapping, point (ii), we confirm the arguments of Sader et al. (J. Fluid Mech., vol. 793, 2016a) that classical VIV exists when the flag is sufficiently light with respect to the fluid. 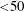We also show that for heavier flags, large-amplitude flapping persists (even for Reynolds numbers ${<}50$) and is not classical VIV. Finally, with respect to point (iii), chaotic flapping has been observed experimentally for Reynolds numbers of 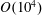$O(10^{4})$, and here we show that chaos also persists at a moderate Reynolds number of 200. We characterise this chaotic regime and calculate its strange attractor, whose structure is controlled by the above-mentioned deformed equilibria and is similar to a Lorenz attractor.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Instability: Instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 857 , 25 December 2018 , pp. 312 - 344
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75, 750–756.Google Scholar
Colonius, T. & Taira, K. 2008 A fast immersed boundary method using a nullspace approach and multi-domain far-field boundary conditions. Comput. Meth. Appl. Mech. Engng 197 (25), 2131–2146.Google Scholar
Connell, B. S. & Yue, D. K. 2007 Flapping dynamics of a flag in a uniform stream. J. Fluid Mech. 581, 33–67.Google Scholar
Criesfield, M. A. 1991 Non-Linear Finite Element Analysis of Solids and Structures, vol. 1. Wiley.Google Scholar
Degroote, J., Bathe, K.-J. & Vierendeels, J. 2009 Performance of a new partitioned procedure versus a monolithic procedure in fluid–structure interaction. Comput. Struct. 87 (11), 793–801.Google Scholar
Goza, A. & Colonius, T. 2017 A strongly-coupled immersed-boundary formulation for thin elastic structures. J. Comput. Phys. 336, 401–411.Google Scholar
Gurugubelli, P. S. & Jaiman, R. K. 2015 Self-induced flapping dynamics of a flexible inverted foil in a uniform flow. J. Fluid Mech. 781, 657–694.Google Scholar
Gurugubelli, P. S. & Jaiman, R. K.2017 On the mechanism of large amplitude flapping of inverted foil in a uniform flow. arXiv:1711.01065.Google Scholar
Khalak, A. & Williamson, C. H. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13, 813–851.Google Scholar
Kim, D., Cossé, J., Cerdeira, C. H. & Gharib, M. 2013 Flapping dynamics of an inverted flag. J. Fluid Mech. 736, R1.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.Google Scholar
Mittal, S. & Singh, S. 2005 Vortex-induced vibrations at subcritical Re . J. Fluid Mech. 534, 185–194.Google Scholar
Roshko, A.1954 On the drag and shedding frequency of two-dimensional bluff bodies. Tech. Rep. National Advisory Committee for Aeronautics, Washington, DC, United States.Google Scholar
Ryu, J., Park, S. G., Kim, B. & Sung, H. J. 2015 Flapping dynamics of an inverted flag in a uniform flow. J. Fluids Struct. 57, 159–169.Google Scholar
Sader, J. E. 1998 Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 84 (1), 64–76.Google Scholar
Sader, J. E., Cossé, J., Kim, D., Fan, B. & Gharib, M. 2016a Large-amplitude flapping of an inverted flag in a uniform steady flow: a vortex-induced vibration. J. Fluid Mech. 793, 524–555.Google Scholar
Sader, J. E., Huertas-Cerdeira, C. & Gharib, M. 2016b Stability of slender inverted flags and rods in uniform steady flow. J. Fluid Mech. 809, 873–894.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19, 389–447.Google Scholar
Shelley, M. J. & Zhang, J. 2011 Flapping and bending bodies interacting with fluid flows. Annu. Rev. Fluid Mech. 43, 449–465.Google Scholar
Shen, N., Chakraborty, D. & Sader, J. E. 2016 Resonant frequencies of cantilevered sheets under various clamping configurations immersed in fluid. J. Appl. Phys. 120, 144504.Google Scholar
Shoele, K. & Mittal, R. 2016 Energy harvesting by flow-induced flutter in a simple model of an inverted piezoelectric flag. J. Fluid Mech. 790, 582–606.Google Scholar
Strogatz, S. H. 1994 Nonlinear Dynamics and Chaos. Perseus.Google Scholar
Taneda, S. 1968 Waving motions of flags. J. Phys. Soc. Japan 24 (2), 392–401.Google Scholar
Tian, F.-B., Dai, H., Luo, H., Doyle, J. F. & Rousseau, B. 2014 Fluid–structure interaction involving large deformations: 3D simulations and applications to biological systems. J. Comput. Phys. 258, 451–469.Google Scholar
Williamson, C. H. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.Google Scholar
Wolf, A., Swift, J. B., Swinney, H. L. & Vastano, J. A. 1985 Determining Lyapunov exponents from a time series. Physica D 16 (3), 285–317.Google Scholar