Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T03:49:02.490Z Has data issue: false hasContentIssue false
  • English
  • Français

A global linearized framework for modelling shear dispersion and turbulent diffusion of passive scalar fluctuations

Published online by Cambridge University Press:  29 March 2021

Thomas Ludwig Kaiser Open the ORCID record for Thomas Ludwig Kaiser [Opens in a new window]  and
Kilian Oberleithner Open the ORCID record for Kilian Oberleithner [Opens in a new window]
Thomas Ludwig Kaiser*
Affiliation:
Laboratory of Flow Instabilities and Dynamics, TU Berlin, 10623Berlin, Germany
Kilian Oberleithner
Affiliation:
Laboratory of Flow Instabilities and Dynamics, TU Berlin, 10623Berlin, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

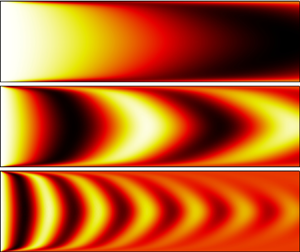
In the field of gas-turbine engineering, entropy waves and fluctuations in fuel–air mixing are of significant importance. The impact of either mechanism on thermoacoustic stability of the engine and combustion noise considerably depends on how they are convected in the combustion chamber. In this work, a novel method is employed to analyse their convection. Both effects are modelled using a transport equation of a passive scalar linearized around the mean field. The linearized transport equation is discretized using finite elements. It is shown that turbulent passive scalar transport can be described by an eddy diffusivity in the linear framework. The method is furthermore validated against direct numerical simulation (DNS) of passive scalar transport in a turbulent channel flow. Taking the mean flow from the DNS as input, the method reproduces transport of periodic passive scalar fluctuations with high accuracy at negligible numerical expense. Previous studies investigated destructive interference of the passive scalar due to a non-uniform mean flow profile, a process termed mean flow shear dispersion. The method introduced in this study, however, allows us to additionally quantify the impact of molecular and turbulent diffusion. For the channel flow under investigation, mean flow shear dispersion is the dominant mechanism at low frequencies while, at higher frequencies, turbulent diffusion needs to be accounted for to reproduce the DNS results. Molecular diffusion, however, only has a minor effect on the overall convection in the turbulent channel flow.

JFM classification

Mixing: Turbulent mixing Turbulent Flows: Turbulence modelling Reacting Flows: Turbulent reacting flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A111
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alnæs, M.S., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, M.E. & Wells, G.N. 2015 The fenics project version 1.5. Arch. Numer. Softw. 3 (100), 9–23.Google Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.CrossRefGoogle Scholar
Bluemner, R., Paschereit, C.O. & Oberleithner, K. 2019 Generation and transport of equivalence ratio fluctuations in an acoustically forced swirl burner. Combust. Flame 209, 99–116.CrossRefGoogle Scholar
Bohn, M.S. 1976 Noise produced by the interaction of acoustic waves and entropy waves with high-speed nozzle flows. PhD thesis, California Institute of Technology.Google Scholar
Cess, R.D. 1958 A survey of the literature on heat transfer in turbulent tube flow. Research Report 8–0529.Google Scholar
Chen, L.S., Bomberg, S. & Polifke, W. 2016 Propagation and generation of acoustic and entropy waves across a moving flame front. Combust. Flame 166, 170–180.CrossRefGoogle Scholar
Ćosić, B., Terhaar, S., Moeck, J.P. & Paschereit, C.O. 2015 Response of a swirl-stabilized flame to simultaneous perturbations in equivalence ratio and velocity at high oscillation amplitudes. Combust. Flame 162 (4), 1046–1062.CrossRefGoogle Scholar
Crouch, J.D., Garbaruk, A. & Magidov, D. 2007 Predicting the onset of flow unsteadiness based on global instability. J. Comput. Phys. 224 (2), 924–940.CrossRefGoogle Scholar
Cumpsty, N.A., Marble, F.E. & Hawthorne, W.R. 1977 The interaction of entropy fluctuations with turbine blade rows; a mechanism of turbojet engine noise. Proc. R. Soc. Lond. A 357 (1690), 323–344.Google Scholar
Dowling, A.P. & Mahmoudi, Y. 2015 Combustion noise. Proc. Combust. Inst. 35 (1), 65–100.CrossRefGoogle Scholar
Dowling, A.P. & Stow, S.R. 2003 Acoustic analysis of gas turbine combustors. J. Propul. Power 19 (5), 751–764.CrossRefGoogle Scholar
Giusti, A., Worth, N.A., Mastorakos, E. & Dowling, A.P. 2017 Experimental and numerical investigation into the propagation of entropy waves. AIAA J. 55 (2), 446–458.CrossRefGoogle Scholar
Goh, C.S. & Morgans, A.S. 2013 The influence of entropy waves on the thermoacoustic stability of a model combustor. Combust. Sci. Technol. 185 (2), 249–268.CrossRefGoogle Scholar
Hermeth, S., Staffelbach, G., Gicquel, L. & Poinsot, T. 2013 LES evaluation of the effects of equivalence ratio fluctuations on the dynamic flame response in a real gas turbine combustion chamber. Proc. Combust. Inst. 34 (2), 3165–3173.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to ${Re}_{\tau }=2003$. Phys. Fluids 18 (1), 011702.CrossRefGoogle Scholar
Huber, A. & Polifke, W. 2009 a Dynamics of practical premixed flames, Part I: model structure and identification. Intl J. Spray Combust. 1 (2), 199–228.CrossRefGoogle Scholar
Huber, A. & Polifke, W. 2009 b Dynamics of practical premixed flames, Part II: identification and interpretation of CFD data. Intl J. Spray Combust. 1 (2), 229–249.CrossRefGoogle Scholar
Hussain, A.K.M.F. & Reynolds, W.C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41 (2), 241–258.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.CrossRefGoogle Scholar
Illingworth, S.J., Monty, J.P. & Marusic, I. 2018 Estimating large-scale structures in wall turbulence using linear models. J. Fluid Mech. 842, 146–162.CrossRefGoogle Scholar
Kaiser, T.L., Lesshafft, L. & Oberleithner, K. 2019 a Prediction of the flow response of a turbulent flame to acoustic pertubations based on mean flow resolvent analysis. Trans. ASME: J. Engng Gas Turbines Power 141 (11), 111021.Google Scholar
Kaiser, T.L., Oberleithner, K., Selle, L. & Poinsot, T. 2019 b Examining the effect of geometry changes in industrial fuel injection systems on hydrodynamic structures with biglobal linear stability analysis. Trans. ASME: J. Engng Gas Turbines Power 142 (1), 011024.Google Scholar
Kays, W.M. 1994 Turbulent Prandtl number—where are we? Trans. ASME: J. Heat Transfer 116 (2), 284–295.CrossRefGoogle Scholar
Lieuwen, T., Neumeier, Y. & Zinn, B.T. 1998 The role of unmixedness and chemical kinetics in driving combustion instabilities in lean premixed combustors. Combust. Sci. Technol. 135 (1–6), 193–211.CrossRefGoogle Scholar
Lieuwen, T. & Zinn, B.T. 1998 The role of equivalence ratio oscillations in driving combustion instabilities in low $\textrm {NO}_x$ gas turbines. Proc. Combust. Inst. 27 (2), 1809–1816.CrossRefGoogle Scholar
Marble, F.E. & Candel, S.M. 1977 Acoustic disturbance from gas non-uniformities convected through a nozzle. J. Sound Vib. 55 (2), 225–243.CrossRefGoogle Scholar
Martin, R.J. & Brown, N.J. 1990 Analysis and modeling of nitrous oxide chemistry in lean, premixed combustion. Combust. Flame 82 (3), 312–333.CrossRefGoogle Scholar
Martini, E., Cavalieri, A.V.G., Jordan, P., Towne, A. & Lesshafft, L. 2020 Resolvent-based optimal estimation of transitional and turbulent flows. J. Fluid Mech. 900, A2.CrossRefGoogle Scholar
McKeon, B.J. & Sharma, A.S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Moase, W.H., Brear, M.J. & Manzie, C. 2007 The forced response of choked nozzles and supersonic diffusers. J. Fluid Mech. 585, 281–304.CrossRefGoogle Scholar
Morgans, A.S. & Duran, I. 2016 Entropy noise: a review of theory, progress and challenges. Intl J. Spray Combust. 8 (4), 285–298.CrossRefGoogle Scholar
Morgans, A.S., Goh, C.S. & Dahan, J.A. 2013 The dissipation and shear dispersion of entropy waves in combustor thermoacoustics. J. Fluid Mech. 733, R2.CrossRefGoogle Scholar
Morra, P., Nogueira, P.A.S., Cavalieri, A.V.G. & Henningson, D.S. 2021 The colour of forcing statistics in resolvent analyses of turbulent channel flows. J. Fluid Mech. 907, A24.CrossRefGoogle Scholar
Morra, P., Semeraro, O., Henningson, D.S. & Cossu, C. 2019 On the relevance of reynolds stresses in resolvent analyses of turbulent wall-bounded flows. J. Fluid Mech. 867, 969–984.CrossRefGoogle Scholar
Moser, R.D., Kim, J. & Mansour, N.N. 1998 Database: direct numerical simulation of turbulent channel flow up to ${Re}_{\tau }=590$. https://torroja.dmt.upm.es/turbdata/agard/chapter5/PCH10, [Online; accessed May 14, 2020].Google Scholar
Moser, R.D., Kim, J. & Mansour, N.N 1999 Direct numerical simulation of turbulent channel flow up to ${Re}_{\tau }= 590$. Phys. Fluids 11 (4), 943–945.CrossRefGoogle Scholar
Motheau, E., Nicoud, F. & Poinsot, T. 2014 Mixed acoustic–entropy combustion instabilities in gas turbines. J. Fluid Mech. 749, 542–576.CrossRefGoogle Scholar
Oberleithner, K., Paschereit, C.O. & Wygnanski, I. 2014 On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 741, 156–199.CrossRefGoogle Scholar
Pickering, E.M., Rigas, G., Sipp, D., Schmidt, O.T. & Colonius, T. 2019 Eddy viscosity for resolvent-based jet noise models. In 25th AIAA/CEAS Aeroacoustics Conference, p. 2454.Google Scholar
Poinsot, T. 2017 Prediction and control of combustion instabilities in real engines. Proc. Combust. Inst. 36 (1), 1–28.CrossRefGoogle Scholar
Polifke, W., Paschereit, C.O. & Döbbeling, K. 2001 Constructive and destructive interference of acoustic and entropy waves in a premixed combustor with a choked exit. Intl J. Acoust. Vib. 6 (3), 135–146.Google Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Reynolds, W.C. & Hussain, A.K.M.F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.CrossRefGoogle Scholar
Reynolds, W.C. & Tiederman, W.G. 1967 Stability of turbulent channel flow, with application to Malkus's theory. J. Fluid Mech. 27 (2), 253–272.CrossRefGoogle Scholar
Sattelmayer, T. 2002 Influence of the combustor aerodynamics on combustion instabilities from equivalence ratio fluctuations. Trans. ASME: J. Engng Gas Turbines Power 125 (1), 11–19.Google Scholar
Shih, W.P., Lee, J.G. & Santavicca, D.A. 1996 Stability and emissions characteristics of a lean premixed gas turbine combustor. Symp. (Intl) Combust. 26 (2), 2771–2778.CrossRefGoogle Scholar
Strahle, W.C. 1978 Combustion noise. Prog. Energy Combust. 4 (3), 157–176.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M.P. 2016 Coherent structures in a swirl injector at $Re = 4800$ by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Venkataraman, K.K., Preston, L.H., Simons, D.W., Lee, B.J., Lee, J.G. & Santavicca, D.A. 1999 Mechanism of combustion instability in a lean premixed dump combustor. J. Propul. Power 15 (6), 909–918.CrossRefGoogle Scholar
Viola, F., Iungo, G.V., Camarri, S., Porté-Agel, F. & Gallaire, F. 2014 Prediction of the hub vortex instability in a wind turbine wake: stability analysis with eddy-viscosity models calibrated on wind tunnel data. J. Fluid Mech. 750, R1.CrossRefGoogle Scholar
Wassmer, D., Schuermans, B., Paschereit, C.O. & Moeck, J.P. 2017 Measurement and modeling of the generation and the transport of entropy waves in a model gas turbine combustor. Intl J. Spray Combust. 9 (4), 299–309.CrossRefGoogle Scholar
Xia, Y., Duran, I., Morgans, A.S. & Han, X. 2018 Dispersion of entropy perturbations transporting through an industrial gas turbine combustor. Flow Turbul. Combust. 100 (2), 481–502.CrossRefGoogle ScholarPubMed