Article contents
The generalized Onsager model for the secondary flow in a high-speed rotating cylinder
Published online by Cambridge University Press: 26 September 2011
Abstract
The generalizations of the Onsager model for the radial boundary layer and the Carrier–Maslen model for the end-cap axial boundary layer in a high-speed rotating cylinder are formulated for studying the secondary gas flow due to wall heating and due to insertion of mass, momentum and energy into the cylinder. The generalizations have wider applicability than the original Onsager and Carrier–Maslen models, because they are not restricted to the limit 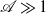 , though they are restricted to the limit
, though they are restricted to the limit 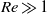 and a high-aspect-ratio cylinder whose length/diameter ratio is large. Here, the stratification parameter
and a high-aspect-ratio cylinder whose length/diameter ratio is large. Here, the stratification parameter 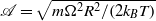 . This parameter
. This parameter 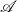 is the ratio of the peripheral speed,
is the ratio of the peripheral speed, 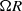 , to the most probable molecular speed,
, to the most probable molecular speed, 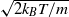 , the Reynolds number
, the Reynolds number 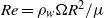 , where
, where 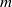 is the molecular mass,
is the molecular mass, 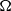 and
and 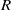 are the rotational speed and radius of the cylinder,
are the rotational speed and radius of the cylinder, 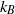 is the Boltzmann constant,
is the Boltzmann constant, 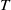 is the gas temperature,
is the gas temperature, 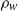 is the gas density at wall, and
is the gas density at wall, and 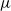 is the gas viscosity. In the case of wall forcing, analytical solutions are obtained for the sixth-order generalized Onsager equations for the master potential, and for the fourth-order generalized Carrier–Maslen equation for the velocity potential. For the case of mass/momentum/energy insertion into the flow, the separation-of-variables procedure is used, and the appropriate homogeneous boundary conditions are specified so that the linear operators in the axial and radial directions are self-adjoint. The discrete eigenvalues and eigenfunctions of the linear operators (sixth-order and second-order in the radial and axial directions for the Onsager equation, and fourth-order and second-order in the axial and radial directions for the Carrier–Maslen equation) are determined. These solutions are compared with direct simulation Monte Carlo (DSMC) simulations. The comparison reveals that the boundary conditions in the simulations and analysis have to be matched with care. The commonly used ‘diffuse reflection’ boundary conditions at solid walls in DSMC simulations result in a non-zero slip velocity as well as a ‘temperature slip’ (gas temperature at the wall is different from wall temperature). These have to be incorporated in the analysis in order to make quantitative predictions. In the case of mass/momentum/energy sources within the flow, it is necessary to ensure that the homogeneous boundary conditions are accurately satisfied in the simulations. When these precautions are taken, there is excellent agreement between analysis and simulations, to within 10 %, even when the stratification parameter is as low as 0.707, the Reynolds number is as low as 100 and the aspect ratio (length/diameter) of the cylinder is as low as 2, and the secondary flow velocity is as high as 0.2 times the maximum base flow velocity. The predictions of the generalized models are also significantly better than those of the original Onsager and Carrier–Maslen models, which are restricted to thin boundary layers in the limit of high stratification parameter.
is the gas viscosity. In the case of wall forcing, analytical solutions are obtained for the sixth-order generalized Onsager equations for the master potential, and for the fourth-order generalized Carrier–Maslen equation for the velocity potential. For the case of mass/momentum/energy insertion into the flow, the separation-of-variables procedure is used, and the appropriate homogeneous boundary conditions are specified so that the linear operators in the axial and radial directions are self-adjoint. The discrete eigenvalues and eigenfunctions of the linear operators (sixth-order and second-order in the radial and axial directions for the Onsager equation, and fourth-order and second-order in the axial and radial directions for the Carrier–Maslen equation) are determined. These solutions are compared with direct simulation Monte Carlo (DSMC) simulations. The comparison reveals that the boundary conditions in the simulations and analysis have to be matched with care. The commonly used ‘diffuse reflection’ boundary conditions at solid walls in DSMC simulations result in a non-zero slip velocity as well as a ‘temperature slip’ (gas temperature at the wall is different from wall temperature). These have to be incorporated in the analysis in order to make quantitative predictions. In the case of mass/momentum/energy sources within the flow, it is necessary to ensure that the homogeneous boundary conditions are accurately satisfied in the simulations. When these precautions are taken, there is excellent agreement between analysis and simulations, to within 10 %, even when the stratification parameter is as low as 0.707, the Reynolds number is as low as 100 and the aspect ratio (length/diameter) of the cylinder is as low as 2, and the secondary flow velocity is as high as 0.2 times the maximum base flow velocity. The predictions of the generalized models are also significantly better than those of the original Onsager and Carrier–Maslen models, which are restricted to thin boundary layers in the limit of high stratification parameter.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 26
- Cited by


