Article contents
The generalized Onsager model for a binary gas mixture
Published online by Cambridge University Press: 23 July 2014
Abstract
The Onsager model for the secondary flow field in a high-speed rotating cylinder is extended to incorporate the difference in mass of the two species in a binary gas mixture. The base flow is an isothermal solid-body rotation in which there is a balance between the radial pressure gradient and the centrifugal force density for each species. Explicit expressions for the radial variation of the pressure, mass/mole fractions, and from these the radial variation of the viscosity, thermal conductivity and diffusion coefficient, are derived, and these are used in the computation of the secondary flow. For the secondary flow, the mass, momentum and energy equations in axisymmetric coordinates are expanded in an asymptotic series in a parameter 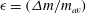 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\epsilon = (\Delta m/ m_{av})$, where
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\epsilon = (\Delta m/ m_{av})$, where 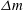 $\Delta m$ is the difference in the molecular masses of the two species, and the average molecular mass
$\Delta m$ is the difference in the molecular masses of the two species, and the average molecular mass 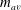 $m_{av}$ is defined as
$m_{av}$ is defined as 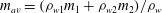 $m_{av}= (\rho _{w1} m_1 + \rho _{w2} m_2)/\rho _w$, where
$m_{av}= (\rho _{w1} m_1 + \rho _{w2} m_2)/\rho _w$, where 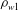 $\rho _{w1}$ and
$\rho _{w1}$ and 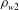 $\rho _{w2}$ are the mass densities of the two species at the wall, and
$\rho _{w2}$ are the mass densities of the two species at the wall, and 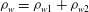 $\rho _w = \rho _{w1} + \rho _{w2}$. The equation for the master potential and the boundary conditions are derived correct to
$\rho _w = \rho _{w1} + \rho _{w2}$. The equation for the master potential and the boundary conditions are derived correct to 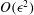 $O(\epsilon ^2)$. The leading-order equation for the master potential contains a self-adjoint sixth-order operator in the radial direction, which is different from the generalized Onsager model (Pradhan & Kumaran, J. Fluid Mech., vol. 686, 2011, pp. 109–159), since the species mass difference is included in the computation of the density, viscosity and thermal conductivity in the base state. This is solved, subject to boundary conditions, to obtain the leading approximation for the secondary flow, followed by a solution of the diffusion equation for the leading correction to the species mole fractions. The
$O(\epsilon ^2)$. The leading-order equation for the master potential contains a self-adjoint sixth-order operator in the radial direction, which is different from the generalized Onsager model (Pradhan & Kumaran, J. Fluid Mech., vol. 686, 2011, pp. 109–159), since the species mass difference is included in the computation of the density, viscosity and thermal conductivity in the base state. This is solved, subject to boundary conditions, to obtain the leading approximation for the secondary flow, followed by a solution of the diffusion equation for the leading correction to the species mole fractions. The 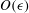 $O(\epsilon )$ and
$O(\epsilon )$ and 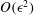 $O(\epsilon ^2)$ equations contain inhomogeneous terms that depend on the lower-order solutions, and these are solved in a hierarchical manner to obtain the
$O(\epsilon ^2)$ equations contain inhomogeneous terms that depend on the lower-order solutions, and these are solved in a hierarchical manner to obtain the 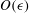 $O(\epsilon )$ and
$O(\epsilon )$ and 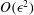 $O(\epsilon ^2)$ corrections to the master potential. A similar hierarchical procedure is used for the Carrier–Maslen model for the end-cap secondary flow. The results of the Onsager hierarchy, up to
$O(\epsilon ^2)$ corrections to the master potential. A similar hierarchical procedure is used for the Carrier–Maslen model for the end-cap secondary flow. The results of the Onsager hierarchy, up to 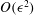 $O(\epsilon ^2)$, are compared with the results of direct simulation Monte Carlo simulations for a binary hard-sphere gas mixture for secondary flow due to a wall temperature gradient, inflow/outflow of gas along the axis, as well as mass and momentum sources in the flow. There is excellent agreement between the solutions for the secondary flow correct to
$O(\epsilon ^2)$, are compared with the results of direct simulation Monte Carlo simulations for a binary hard-sphere gas mixture for secondary flow due to a wall temperature gradient, inflow/outflow of gas along the axis, as well as mass and momentum sources in the flow. There is excellent agreement between the solutions for the secondary flow correct to 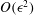 $O(\epsilon ^2)$ and the simulations, to within 15 %, even at a Reynolds number as low as 100, and length/diameter ratio as low as 2, for a low stratification parameter
$O(\epsilon ^2)$ and the simulations, to within 15 %, even at a Reynolds number as low as 100, and length/diameter ratio as low as 2, for a low stratification parameter 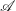 $\mathcal{A}$ of 0.707, and when the secondary flow velocity is as high as 0.2 times the maximum base flow velocity, and the ratio
$\mathcal{A}$ of 0.707, and when the secondary flow velocity is as high as 0.2 times the maximum base flow velocity, and the ratio 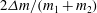 $2 \Delta m / (m_1 + m_2)$ is as high as 0.5. Here, the Reynolds number
$2 \Delta m / (m_1 + m_2)$ is as high as 0.5. Here, the Reynolds number 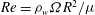 $\mathit{Re}= \rho _w \varOmega R^2 / \mu $, the stratification parameter
$\mathit{Re}= \rho _w \varOmega R^2 / \mu $, the stratification parameter 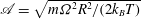 $\mathcal{A}= \sqrt{m \varOmega ^2 R^2 / (2k_BT)}$,
$\mathcal{A}= \sqrt{m \varOmega ^2 R^2 / (2k_BT)}$, 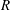 $R$ and
$R$ and 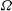 $\varOmega $ are the cylinder radius and angular velocity,
$\varOmega $ are the cylinder radius and angular velocity,  $m$ is the molecular mass,
$m$ is the molecular mass, 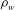 $\rho _w$ is the wall density,
$\rho _w$ is the wall density, 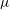 $\mu $ is the viscosity and
$\mu $ is the viscosity and 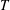 $T$ is the temperature. The leading-order solutions do capture the qualitative trends, but are not in quantitative agreement.
$T$ is the temperature. The leading-order solutions do capture the qualitative trends, but are not in quantitative agreement.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
Footnotes
This work forms part of the PhD Thesis of Sahadev Pradhan, Indian Institute of Science, 2014.
References
- 14
- Cited by


