Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zuk, P. J.
Wajnryb, E.
Mizerski, K. A.
and
Szymczak, P.
2014.
Rotne–Prager–Yamakawa approximation for different-sized particles in application to macromolecular bead models.
Journal of Fluid Mechanics,
Vol. 741,
Issue. ,
Jibuti, Levan
Qi, Ling
Misbah, Chaouqi
Zimmermann, Walter
Rafaï, Salima
and
Peyla, Philippe
2014.
Self-focusing and jet instability of a microswimmer suspension.
Physical Review E,
Vol. 90,
Issue. 6,
Mizerski, Krzysztof A.
Wajnryb, Eligiusz
Zuk, Pawel J.
and
Szymczak, Piotr
2014.
The Rotne-Prager-Yamakawa approximation for periodic systems in a shear flow.
The Journal of Chemical Physics,
Vol. 140,
Issue. 18,
Delmotte, Blaise
Climent, Eric
and
Plouraboué, Franck
2015.
A general formulation of Bead Models applied to flexible fibers and active filaments at low Reynolds number.
Journal of Computational Physics,
Vol. 286,
Issue. ,
p.
14.
Długosz, Maciej
and
Antosiewicz, Jan M.
2015.
Toward an Accurate Modeling of Hydrodynamic Effects on the Translational and Rotational Dynamics of Biomolecules in Many-Body Systems.
The Journal of Physical Chemistry B,
Vol. 119,
Issue. 26,
p.
8425.
Uematsu, Yuki
2015.
Nonlinear electro-osmosis of dilute non-adsorbing polymer solutions with low ionic strength.
Soft Matter,
Vol. 11,
Issue. 37,
p.
7402.
Delong, Steven
Balboa Usabiaga, Florencio
and
Donev, Aleksandar
2015.
Brownian dynamics of confined rigid bodies.
The Journal of Chemical Physics,
Vol. 143,
Issue. 14,
Balboa Usabiaga, Florencio
Kallemov, Bakytzhan
Delmotte, Blaise
Bhalla, Amneet
Griffith, Boyce
and
Donev, Aleksandar
2016.
Hydrodynamics of suspensions of passive and active rigid particles: a rigid multiblob approach.
Communications in Applied Mathematics and Computational Science,
Vol. 11,
Issue. 2,
p.
217.
Lisicki, Maciej
and
Nägele, Gerhard
2016.
Soft Matter at Aqueous Interfaces.
Vol. 917,
Issue. ,
p.
313.
Mizerski, Krzysztof A.
and
Wajnryb, Eligiusz
2016.
Short-time self-diffusion, collective diffusion and effective viscosity of dilute hard sphere magnetic suspensions.
Journal of Fluid Mechanics,
Vol. 791,
Issue. ,
p.
237.
Goddard, B. D.
Nold, A.
and
Kalliadasis, S.
2016.
Dynamical density functional theory with hydrodynamic interactions in confined geometries.
The Journal of Chemical Physics,
Vol. 145,
Issue. 21,
Ivenso, Ikenna D.
2016.
Modeling the Abrupt Buckling Transition in dsDNA During Supercoiling.
Journal of Computational and Nonlinear Dynamics,
Vol. 11,
Issue. 6,
Kallemov, Bakytzhan
Bhalla, Amneet
Griffith, Boyce
and
Donev, Aleksandar
2016.
An immersed boundary method for rigid bodies.
Communications in Applied Mathematics and Computational Science,
Vol. 11,
Issue. 1,
p.
79.
Ivenso, Ikenna D.
2017.
Extensional Response and Equilibrium Kinetics of Torsionally Relaxed dsDNA Under Tension: A Brownian Dynamics Study.
Journal of Computational and Nonlinear Dynamics,
Vol. 12,
Issue. 3,
Vutukuri, Hanumantha Rao
Bet, Bram
van Roij, René
Dijkstra, Marjolein
and
Huck, Wilhelm T. S.
2017.
Rational design and dynamics of self-propelled colloidal bead chains: from rotators to flagella.
Scientific Reports,
Vol. 7,
Issue. 1,
Fiore, Andrew M.
Balboa Usabiaga, Florencio
Donev, Aleksandar
and
Swan, James W.
2017.
Rapid sampling of stochastic displacements in Brownian dynamics simulations.
The Journal of Chemical Physics,
Vol. 146,
Issue. 12,
Zuk, Pawel J.
Cichocki, Bogdan
and
Szymczak, Piotr
2017.
Intrinsic viscosity of macromolecules within the generalized Rotne–Prager–Yamakawa approximation.
Journal of Fluid Mechanics,
Vol. 822,
Issue. ,
Winkler, Roland G.
Elgeti, Jens
and
Gompper, Gerhard
2017.
Active Polymers — Emergent Conformational and Dynamical Properties: A Brief Review.
Journal of the Physical Society of Japan,
Vol. 86,
Issue. 10,
p.
101014.
Balboa Usabiaga, Florencio
Delmotte, Blaise
and
Donev, Aleksandar
2017.
Brownian dynamics of confined suspensions of active microrollers.
The Journal of Chemical Physics,
Vol. 146,
Issue. 13,
Uematsu, Yuki
2017.
Electro-Osmosis of Polymer Solutions.
p.
51.
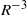 ${R}^{- 3} $ or slower in interparticle distances) and that the diffusion matrix is positive definite, which is essential for Brownian dynamics modelling. Here, we extend the Rotne–Prager–Yamakawa approach to include both translational and rotational degrees of freedom, and derive the regularizing corrections to account for overlapping particles. Additionally, we show how the Rotne–Prager–Yamakawa approximation can be generalized for other geometries and boundary conditions.
${R}^{- 3} $ or slower in interparticle distances) and that the diffusion matrix is positive definite, which is essential for Brownian dynamics modelling. Here, we extend the Rotne–Prager–Yamakawa approach to include both translational and rotational degrees of freedom, and derive the regularizing corrections to account for overlapping particles. Additionally, we show how the Rotne–Prager–Yamakawa approximation can be generalized for other geometries and boundary conditions.

