Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T14:26:18.879Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalised higher-order Kolmogorov scales

Published online by Cambridge University Press:  30 March 2016

Jonas Boschung ,
Fabian Hennig ,
Michael Gauding ,
Heinz Pitsch  and
Norbert Peters
Jonas Boschung*
Affiliation:
Institute for Combustion Technology, RWTH Aachen University, Templergraben 64, Aachen, Germany
Fabian Hennig
Affiliation:
Institute for Combustion Technology, RWTH Aachen University, Templergraben 64, Aachen, Germany
Michael Gauding
Affiliation:
Chair of Numerical Thermo-Fluid Dynamics, TU Bergakademie, Fuchsmühlenweg 9, Freiberg, Germany
Heinz Pitsch
Affiliation:
Institute for Combustion Technology, RWTH Aachen University, Templergraben 64, Aachen, Germany
Norbert Peters
Affiliation:
Institute for Combustion Technology, RWTH Aachen University, Templergraben 64, Aachen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Kolmogorov introduced dissipative scales based on the mean dissipation 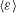$\langle {\it\varepsilon}\rangle$ and the viscosity ${\it\nu}$, namely the Kolmogorov length 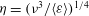${\it\eta}=({\it\nu}^{3}/\langle {\it\varepsilon}\rangle )^{1/4}$ and the velocity 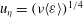$u_{{\it\eta}}=({\it\nu}\langle {\it\varepsilon}\rangle )^{1/4}$. However, the existence of smaller scales has been discussed in the literature based on phenomenological intermittency models. Here, we introduce exact dissipative scales for the even-order longitudinal structure functions. The derivation is based on exact relations between even-order moments of the longitudinal velocity gradient 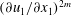$(\partial u_{1}/\partial x_{1})^{2m}$ and the dissipation 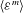$\langle {\it\varepsilon}^{m}\rangle$. We then find a new length scale 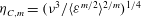${\it\eta}_{C,m}=({\it\nu}^{3}/\langle {\it\varepsilon}^{m/2}\rangle ^{2/m})^{1/4}$ and 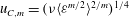$u_{C,m}=({\it\nu}\langle {\it\varepsilon}^{m/2}\rangle ^{2/m})^{1/4}$, i.e. the dissipative scales depend rather on the moments of the dissipation 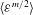$\langle {\it\varepsilon}^{m/2}\rangle$ and thus the full probability density function (p.d.f.) 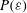$P({\it\varepsilon})$ instead of powers of the mean 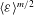$\langle {\it\varepsilon}\rangle ^{m/2}$. The results presented here are exact for longitudinal even-ordered structure functions under the assumptions of (local) isotropy, (local) homogeneity and incompressibility, and we find them to hold empirically also for the mixed and transverse as well as odd orders. We use direct numerical simulations (DNS) with Reynolds numbers from 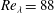$Re_{{\it\lambda}}=88$ up to 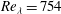$Re_{{\it\lambda}}=754$ to compare the different scalings. We find that indeed 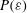$P({\it\varepsilon})$ or, more precisely, the scaling of 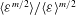$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$ as a function of the Reynolds number is a key parameter, as it determines the ratio 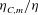${\it\eta}_{C,m}/{\it\eta}$ as well as the scaling of the moments of the velocity gradient p.d.f. As 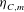${\it\eta}_{C,m}$ is smaller than 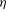${\it\eta}$, this leads to a modification of the estimate of grid points required for DNS.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 794 , 10 May 2016 , pp. 233 - 251
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anselmet, F., Gagne, Y. & Hopfinger, E. 1984 High-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 140 (63), 63–89.Google Scholar
Benzi, R., Ciliberto, S., Baudet, C. & Chavarria, G. R. 1995 On the scaling of three-dimensional homogeneous and isotropic turbulence. Physica D 80 (4), 385–398.Google Scholar
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E 48 (1), R29–R32.CrossRefGoogle ScholarPubMed
Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1 (05), 497–504.CrossRefGoogle Scholar
Boschung, J. 2015 Exact relations between the moments of dissipation and longitudinal velocity derivatives in turbulent flows. Phys. Rev. E 92 (4), 043013.CrossRefGoogle ScholarPubMed
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Donzis, D., Yeung, P. & Sreenivasan, K. 2008 Dissipation and enstrophy in isotropic turbulence: resolution effects and scaling in direct numerical simulations. Phys. Fluids 20 (4), 045108.Google Scholar
Dubrulle, B. 1994 Intermittency in fully developed turbulence: log-Poisson statistics and generalized scale covariance. Phys. Rev. Lett. 73 (7), 959–962.Google Scholar
Eswaran, V. & Pope, S. 1988 Direct numerical simulations of the turbulent mixing of a passive scalar. Phys. Fluids 31, 506–520.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Frisch, U. & Vergassola, M. 1991 A prediction of the multifractal model: the intermediate dissipation range. Europhys. Lett. 14, 439–444.Google Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14, 1065.Google Scholar
Hierro, J. & Dopazo, C. 2003 Fourth-order statistical moments of the velocity gradient tensor in homogeneous, isotropic turbulence. Phys. Fluids 15 (11), 3434–3442.CrossRefGoogle Scholar
Hill, R. J. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434 (1), 379–388.Google Scholar
Hou, T. Y. & Li, R. 2007 Computing nearly singular solutions using pseudo-spectral methods. J. Comput. Phys. 226 (1), 379–397.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
Jiménez, J., Wray, A., Saffman, P. & Rogallo, R. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
de Karman, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164 (917), 192–215.Google Scholar
Kolmogorov, A. N. 1941a Dissipation of energy in locally isotropic turbulence. Dokl. Akad. Nauk. SSSR 32, 16–18.Google Scholar
Kolmogorov, A. N. 1941b The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk. SSSR 30, 299–303.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (1), 82–85.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics, Course of Theoretical Physics, vol. 6. Pergamon.Google Scholar
Li, N. & Laizet, S. 2010 2DECOMP and FFT – a highly scalable 2D decomposition library and FFT interface. In Cray User Group 2010 Conference, pp. 1–13.Google Scholar
Meneveau, C. 1996 Transition between viscous and inertial-range scaling of turbulence structure functions. Phys. Rev. E 54 (4), 3657.Google Scholar
Meneveau, C. & Sreenivasan, K. 1987 Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 59 (13), 1424.Google Scholar
Meneveau, C. & Sreenivasan, K. 1991 The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 224 (429–484), 180.CrossRefGoogle Scholar
Obukhov, A. R. 1962 Some specific features of atmospheric turbulence. J. Fluid Mech. 13, 77–81.Google Scholar
Paladin, G. & Vulpiani, A. 1987a Anomalous scaling laws in multifractal objects. Phys. Rep. 156 (4), 147–225.CrossRefGoogle Scholar
Paladin, G. & Vulpiani, A. 1987b Degrees of freedom of turbulence. Phys. Rev. A 35 (4), 1971.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rotta, J. C. 1972 Turbulente Strömungen, vol. 8. B. G. Teubner.CrossRefGoogle Scholar
Schumacher, J., Scheel, J. D., Krasnov, D., Donzis, D. A., Yakhot, V. & Sreenivasan, K. R. 2014 Small-scale universality in fluid turbulence. Proc. Natl Acad. Sci. USA 111 (30), 10961–10965.Google Scholar
Schumacher, J., Sreenivasan, K. R. & Yakhot, V. 2007 Asymptotic exponents from low-Reynolds-number flows. New J. Phys. 9 (4), 89.Google Scholar
She, Z.-S. & Leveque, E. 1994 Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 72 (3), 336.Google Scholar
She, Z.-S. & Waymire, E. C. 1995 Quantized energy cascade and log-Poisson statistics in fully developed turbulence. Phys. Rev. Lett. 74 (2), 262.Google Scholar
Siggia, E. D. 1981 Invariants for the one-point vorticity and strain rate correlation functions. Phys. Fluids 24 (11), 1934–1936.Google Scholar
Sreenivasan, K. 1991 Fractals and multifractals in fluid turbulence. Annu. Rev. Fluid Mech. 23 (1), 539–604.Google Scholar
Sreenivasan, K. & Antonia, R. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.Google Scholar
Sreenivasan, K. & Kailasnath, P. 1993 An update on the intermittency exponent in turbulence. Phys. Fluids A 5 (2), 512–514.Google Scholar
Townsend, A. 1951 On the fine-scale structure of turbulence. Proc. R. Soc. Lond. A 208 (1095), 534–542.Google Scholar
Yakhot, V. 2001 Mean-field approximation and a small parameter in turbulence theory. Phys. Rev. E 63 (2), 026307.Google Scholar
Yakhot, V. 2003 Pressure–velocity correlations and scaling exponents in turbulence. J. Fluid Mech. 495, 135–143.Google Scholar
Yakhot, V. & Sreenivasan, K. R. 2005 Anomalous scaling of structure functions and dynamic constraints on turbulence simulations. J. Stat. Phys. 121 (5–6), 823–841.Google Scholar
Yeung, P. & Pope, S. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207 (1), 531–586.CrossRefGoogle Scholar