Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-12T09:43:45.683Z Has data issue: false hasContentIssue false
  • English
  • Français

A general self-preservation analysis for decaying homogeneous isotropic turbulence

Published online by Cambridge University Press:  21 May 2015

L. Djenidi  and
R. A. Antonia
L. Djenidi*
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle,  2308 NSW, Australia
R. A. Antonia
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle,  2308 NSW, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A general framework of self-preservation (SP) is established, based on the transport equation of the second-order longitudinal velocity structure function in decaying homogeneous isotropic turbulence (HIT). The analysis introduces the skewness of the longitudinal velocity increment, 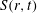$S(r,t)$ ($r$ and $t$ are space increment and time), as an SP controlling parameter. The present SP framework allows a critical appraisal of the specific assumptions that have been made in previous SP analyses. It is shown that SP is achieved when 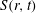$S(r,t)$ varies in a self-similar manner, i.e. 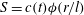$S=c(t){\it\phi}(r/l)$ where 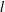$l$ is a scaling length, and 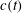$c(t)$ and 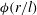${\it\phi}(r/l)$ are dimensionless functions of time and 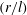$(r/l)$, respectively. When 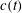$c(t)$ is constant, 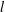$l$ can be identified with the Kolmogorov length scale 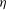${\it\eta}$, even when the Reynolds number is relatively small. On the other hand, the Taylor microscale 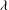${\it\lambda}$ is a relevant SP length scale only when certain conditions are met. The decay law for the turbulent kinetic energy (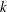$k$) ensuing from the present SP is a generalization of the existing laws and can be expressed as 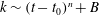$k\sim (t-t_{0})^{n}+B$, where $B$ is a constant representing the energy of the motions whose scales are excluded from the SP range of scales. When 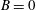$B=0$, SP is achieved at all scales of motion and 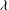${\it\lambda}$ becomes a relevant scaling length together with 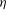${\it\eta}$. The analysis underlines the relation between the initial conditions and the power-law exponent $n$ and also provides a link between them. In particular, an expression relating $n$ to the initial values of the scaling length and velocity is developed. Finally, the present SP analysis is consistent with both experimental grid turbulence data and the eddy-damped quasi-normal Markovian numerical simulation of decaying HIT by Meldi & Sagaut (J. Turbul., vol. 14, 2013, pp. 24–53).

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 773 , 25 June 2015 , pp. 345 - 365
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Burattini, P. 2006 Approach to the 4/5 law in homogeneous isotropic turbulence. J. Fluid Mech. 550, 175–184.CrossRefGoogle Scholar
Antonia, R. A., Djenidi, L. & Danaila, L. 2014 Collapse of the Kolmogorov dissipative range on Kolmogorov scales. Phys. Fluids 26, 045105.CrossRefGoogle Scholar
Antonia, R. A., Lee, S. K., Djenidi, L., Lavoie, P. & Danaila, L. 2013 Invariants for slightly heated decaying turbulence. J. Fluid Mech. 727, 379–406.CrossRefGoogle Scholar
Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2003 Similarity of energy structure functions in decaying homogeneous isotropic turbulence. J. Fluid Mech. 487, 245–269.CrossRefGoogle Scholar
Barenblatt, G. J. & Gavrilov, A. A. 1974 On the theory of self-similar degeneracy of homogeneous isotropic turbulence. Sov. Phys. JETP 38, 399–402.Google Scholar
Batchelor, G. K. 1947 Kolmogorov’s theory of localy isotropic turbulence. Proc. Camb. Phil. Soc. 43, 533–559.CrossRefGoogle Scholar
Batchelor, G. K. 1948 Energy decay and self-preserving correlation functions in isotropic turbulence. Q. Appl. Maths 6, 97–116.CrossRefGoogle Scholar
Batchelor, G. K. 1949 The role of big eddies in homogeneous turbulence. Proc. R. Soc. Lond. A 195, 513–532.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1948 Decay of turbulence in the final period. Proc. R. Soc. Lond. A 194, 527–543.Google Scholar
Bennett, J. C. & Corrsin, S. 1978 Small Reynolds number nearly isotropic turbulence in a straight duct and a contraction. Phys. Fluids 21, 2129–2140.CrossRefGoogle Scholar
Clark, T. T. & Zemach, C. 1995 A spectral model applied to homogeneous turbulence. Phys. Fluids 7, 1674–1694.CrossRefGoogle Scholar
Clark, T. T. & Zemach, C. 1998 Symmetries and the approach to statistical equilibrium in isotropic turbulence. Phys. Fluids 10, 2838–2858.CrossRefGoogle Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotopy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.CrossRefGoogle Scholar
Corrsin, S. 1963 Turbulence: Experimental Methods, vol. 8. Springer.Google Scholar
Djenidi, L. & Antonia, R. A. 2014 Transport equation for the mean turbulent energy dissipation rate in low $R_{{\it\lambda}}$ grid turbulence. J. Fluid Mech. 747, 288–315.CrossRefGoogle Scholar
Djenidi, L., Tardu, S., Antonia, R. A. & Danaila, L. 2014 Breakdown of Kolmogorov’s first similarity hypothesis in grid turbulence. J. Turbul. 15, 596–610.CrossRefGoogle Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids A 4, 1492–1509.CrossRefGoogle Scholar
George, W. K. 2012 Asymptotic effect of initial and upstream conditions on turbulence. Trans. ASME: J. Fluids Engng 134, 061203-1.Google Scholar
Kamruzzaman, Md., Djenidi, L. & Antonia, R. A. 2013 Behaviours of energy spectrum at low Reynolds numbers in grid turbulence. Intl J. Mech. Aerosp. Ind. Mechatron. Engng 7 (12), 1385–1389.Google Scholar
Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164 (917), 192–215.CrossRefGoogle Scholar
Kármán, T. & Lin, C. C. 1949 On the concept of similarity in the theory of isotropic turbulence. Rev. Mod. Phys. 21, 516–519.CrossRefGoogle Scholar
Kolmogorov, A. 1941a On the degeneration (decay) of isotropic turbulence in an incompressible viscous fluid. Dokl. Akad. Nauk SSSR 31, 538–540.Google Scholar
Kolmogorov, A. 1941b Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 16–18.Google Scholar
Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.CrossRefGoogle Scholar
Lin, C. C. 1948 Note on the law of decay of isotropic turbulence. Proc. Natl Acad. Sci. USA 34, 540–543.CrossRefGoogle ScholarPubMed
Meldi, M. & Sagaut, P. 2013 Further insights into self-similarity and self-preservation in freely decaying isotropic tubulence. J. Turbul. 14, 24–53.CrossRefGoogle Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics, vol. 2. MIT Press, reproduced by Dover (2007).Google Scholar
Oberlack, M. 2002 On the decay exponent of isotropic turbulence. Proc. Appl. Maths Mech. 294–297.3.0.CO;2-W>CrossRefGoogle Scholar
Oberlack, M. & Zieleniewicz, A. 2013 Statistical symmetries and its impact on new decay modes and integral invariants of decaying turbulence. J. Turbul. 14, 4–22.CrossRefGoogle Scholar
Ristorcelli, J. R. 2003 The self-preserving decay of isotropic turbulence: analytical solutions for energy and dissipation. Phys. Fluids 15, 3248–3250.CrossRefGoogle Scholar
Ristorcelli, J. R. & Livescu, D. 2004 Decay of isotropic turbulence: fixed points and solutions for nonconstant $G\sim R_{{\it\lambda}}$ palinstrophy. Phys. Fluids 16, 3487–3490.CrossRefGoogle Scholar
Saffman, P. G. 1967a Note on decay of homogeneous turbulence. Phys. Fluids 10, 1349.CrossRefGoogle Scholar
Saffman, P. G. 1967b The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 581–593.CrossRefGoogle Scholar
Saffman, P. G. 1968 Lectures on homogeneous turbulence. In Topics in Nonlinear Physics (ed. Zabusky, N.), pp. 485–614. Springer.CrossRefGoogle Scholar
Sinhuber, M., Bodenschatz, E. & Bewley, G. P. 2015 Decay of turbulence at high Reynolds numbers. Phys. Rev. Lett. 114, 034501.CrossRefGoogle ScholarPubMed
Speziale, C. G. & Bernard, P. 1992 The energy decay in self-preserving isotropic turbulence revisited. J. Fluid Mech. 241, 645–667.CrossRefGoogle Scholar
Vassilicos, J. C. 2011 An infinity of possible invariants for decaying homogeneous turbulence. Phys. Lett. A 6, 1010–1013.CrossRefGoogle Scholar