Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-11T22:46:44.419Z Has data issue: false hasContentIssue false
  • English
  • Français

General procedure for free-surface recovery from bottom pressure measurements: application to rotational overhanging waves

Published online by Cambridge University Press:  30 November 2023

Joris Labarbe Open the ORCID record for Joris Labarbe [Opens in a new window]  and
Didier Clamond Open the ORCID record for Didier Clamond [Opens in a new window]
Joris Labarbe*
Affiliation:
Laboratoire J. A. Dieudonné, Université Côte d'Azur, CNRS UMR 7351, Parc Valrose, 06108 Nice cedex 2, France
Didier Clamond*
Affiliation:
Laboratoire J. A. Dieudonné, Université Côte d'Azur, CNRS UMR 7351, Parc Valrose, 06108 Nice cedex 2, France
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

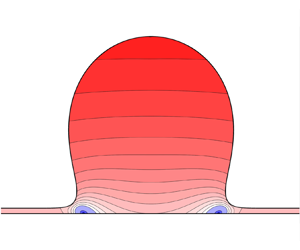
A novel boundary integral approach for the recovery of overhanging (or not) rotational water waves (with constant vorticity) from pressure measurements at the bottom is presented. The method is based on the Cauchy integral formula and on an Eulerian–Lagrangian formalism to accommodate overturning free surfaces. This approach eliminates the need to introduce a priori a special basis of functions, thus providing a general means of fitting the pressure data and, consequently, recovering the free surface. The effectiveness and accuracy of the method are demonstrated through numerical examples.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Mathematical Foundations: Computational methods Geophysical and Geological Flows: Coastal engineering
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 976 , 10 December 2023 , A20
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergan, P.O., Tørum, A. & Traetteberg, A. 1969 Wave measurements by a pressure type wave gauge. Coastal Engng 1968, 19–29.Google Scholar
Boyd, J.P. 2001 Chebyshev and Fourier Spectral Methods. Courier Corporation.Google Scholar
Clamond, D. 2013 New exact relations for easy recovery of steady wave profiles from bottom pressure measurements. J. Fluid Mech. 726, 547–558.CrossRefGoogle Scholar
Clamond, D. 2018 New exact relations for steady irrotational two-dimensional gravity and capillary surface waves. Phil. Trans. R. Soc. A 376 (2111), 20170220.CrossRefGoogle ScholarPubMed
Clamond, D. & Constantin, A. 2013 Recovery of steady periodic wave profiles from pressure measurements at the bed. J. Fluid Mech. 714, 463–475.CrossRefGoogle Scholar
Clamond, D. & Henry, D. 2020 Extreme water-wave profile recovery from pressure measurements at the seabed. J. Fluid Mech. 903, R3.CrossRefGoogle Scholar
Clamond, D., Labarbe, J. & Henry, D. 2023 Recovery of steady rotational wave profiles from pressure measurements at the bed. J. Fluid Mech. 961, R2.CrossRefGoogle Scholar
Constantin, A. 2006 The trajectories of particles in Stokes waves. Invent. Math. 3, 523–535.CrossRefGoogle Scholar
Constantin, A. 2012 On the recovery of solitary wave profiles from pressure measurements. J. Fluid Mech. 699, 376–384.CrossRefGoogle Scholar
Constantin, A. & Strauss, W. 2010 Pressure beneath a Stokes wave. Commun. Pure Appl. Maths 63, 533–557.CrossRefGoogle Scholar
Constantin, A., Strauss, W. & Varvaruca, E. 2016 Global bifurcation of steady gravity water waves with critical layers. Acta Mathematica 217, 195–262.CrossRefGoogle Scholar
Constantin, A. & Varvaruca, E. 2011 Steady periodic water waves with constant vorticity: regularity and local bifurcation. Arch. Rat. Mech. Anal. 199, 33–67.CrossRefGoogle Scholar
Da Silva, A.T. & Peregrine, D.H. 1988 Steep, steady surface waves on water of finite depth with constant vorticity. J. Fluid Mech. 195, 281–302.CrossRefGoogle Scholar
Gakhov, F.D. 1990 Boundary Value Problems. Dover.Google Scholar
Henry, D. 2013 On the pressure transfer function for solitary water waves with vorticity. Math. Ann. 357 (1), 23–30.CrossRefGoogle Scholar
Henry, D. & Thomas, G.P. 2018 Prediction of the free-surface elevation for rotational water waves using the recovery of pressure at the bed. Phil. Trans. R. Soc. A 376, 20170102.CrossRefGoogle ScholarPubMed
Lee, D.Y. & Wang, H. 1985 Measurement of surface waves from subsurface gage. Coast. Engng 1984, 271–286.Google Scholar
Lin, M. & Yang, C. 2020 Ocean observation technologies: A review. Chin. J. Mech. Engng 33 (1), 1–18.Google Scholar
Longuet-Higgins, M.S. 1986 Eulerian and Lagrangian aspects of surface waves. J. Fluid Mech. 173, 683–707.CrossRefGoogle Scholar
Morse, P.M. & Feshbach, H. 1953 Methods of Theoretical Physics. McGraw-Hill.Google Scholar
Oliveras, K.L., Vasan, V., Deconinck, B. & Henderson, D. 2012 Recovering the water-wave profile from pressure measurements. SIAM J. Appl. Maths 72 (3), 897–918.CrossRefGoogle Scholar
Patterson, G.S. Jr. & Orszag, S.A. 1971 Spectral calculations of isotropic turbulence: efficient removal of aliasing interactions. Phys. Fluids 14 (11), 2538–2541.CrossRefGoogle Scholar
Tsai, J.C. & Tsai, C.H. 2009 Wave measurements by pressure transducers using artificial neural network. Ocean Engng 36 (15–16), 1149–1157.CrossRefGoogle Scholar
Vanden-Broeck, J.M. 1994 Steep solitary waves in water of finite depth with constant vorticity. J. Fluid Mech. 274, 339–348.CrossRefGoogle Scholar
Wahlen, E. 2009 Steady water waves with a critical layer. J. Differ. Equ. 246 (6), 2468–2483.CrossRefGoogle Scholar
Wood, D.C. 1992 The computation of polylogarithms. Tech. Rep. 15-92. University of Kent Computing Laboratory.Google Scholar