Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T16:52:55.330Z Has data issue: false hasContentIssue false
  • English
  • Français

The Froude number for solitary water waves with vorticity

Published online by Cambridge University Press:  03 March 2015

Miles H. Wheeler
Miles H. Wheeler*
Affiliation:
Courant Institute of Mathematical Sciences, 251 Mercer Street, New York, NY 10012, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

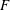We consider two-dimensional solitary water waves on a shear flow with an arbitrary distribution of vorticity. Assuming that the horizontal velocity in the fluid never exceeds the wave speed and that the free surface lies everywhere above its asymptotic level, we give a very simple proof that a suitably defined Froude number $F$ must be strictly greater than the critical value 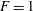$F=1$. We also prove a related upper bound on 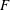$F$, and hence on the amplitude, under more restrictive assumptions on the vorticity.

JFM classification

Waves/Free-surface Flows: Solitary waves Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 768 , 10 April 2015 , pp. 91 - 112
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amick, C. J., Fraenkel, L. E. & Toland, J. F. 1982 On the Stokes conjecture for the wave of extreme form. Acta Mathematica 148, 193–214.Google Scholar
Amick, C. J. & Kirchgässner, K. 1989 A theory of solitary water-waves in the presence of surface tension. Arch. Rat. Mech. Anal. 105 (1), 1–49.Google Scholar
Amick, C. J. & Toland, J. F. 1981 On solitary water-waves of finite amplitude. Arch. Rat. Mech. Anal. 76 (1), 9–95.Google Scholar
Beale, J. T. 1991 Exact solitary water waves with capillary ripples at infinity. Commun. Pure Appl. Maths 44 (2), 211–257.Google Scholar
Bélanger, J.-B. C. J. 1828 Essai sur la Solution Numérique de Quelques Problèmes Relatifs au Mouvement Permanent des eaux Courantes. Carilian-Goeury.Google Scholar
Benjamin, T. B. 1962 The solitary wave on a stream with an arbitrary distribution of vorticity. J. Fluid Mech. 12, 97–116.Google Scholar
Buffoni, B., Groves, M. D. & Toland, J. F. 1996 A plethora of solitary gravity–capillary water waves with nearly critical Bond and Froude numbers. Phil. Trans. R. Soc. Lond. A 354 (1707), 575–607.Google Scholar
Burns, J. C. 1953 Long waves in running water. Math. Proc. Cambridge Philos. Soc. 49 (4), 695–706.Google Scholar
Champneys, A. R., Vanden-Broeck, J.-M. & Lord, G. J. 2002 Do true elevation gravity–capillary solitary waves exist? A numerical investigation. J. Fluid Mech. 454, 403–417.CrossRefGoogle Scholar
Chanson, H. 2009 Development of the Bélanger equation and backwater equation by Jean-Baptiste Bélanger (1828). ASCE J. Hydraul. Engng 135 (3), 159–163.CrossRefGoogle Scholar
Constantin, A. 2011 Nonlinear Water Waves with Applications to Wave–Current Interactions and Tsunamis, CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 81. Society for Industrial and Applied Mathematics (SIAM).Google Scholar
Constantin, A. & Strauss, W. A. 2004 Exact steady periodic water waves with vorticity. Commun. Pure Appl. Maths 57 (4), 481–527.Google Scholar
Constantin, A. & Strauss, W. A. 2011 Periodic traveling gravity water waves with discontinuous vorticity. Arch. Rat. Mech. Anal. 202 (1), 133–175.Google Scholar
Craig, W. & Sternberg, P. 1988 Symmetry of solitary waves. Commun. Part. Diff. Equ. 13 (5), 603–633.CrossRefGoogle Scholar
Craik, A. D. D. 2004 The origins of water wave theory. In Annual Review of Fluid Mechanics, vol. 36, pp. 1–28. Annual Reviews.Google Scholar
Darrigol, O. 2003 The spirited horse, the engineer, and the mathematician: water waves in nineteenth-century hydrodynamics. Arch. Hist. Exact Sci. 58 (1), 21–95.Google Scholar
Ehrnström, M., Escher, J. & Wahlén, E. 2011 Steady water waves with multiple critical layers. SIAM J. Math. Anal. 43 (3), 1436–1456.Google Scholar
Fenton, J. D. 1973 Some results for surface gravity waves on shear flows. IMA J. Appl. Maths 12 (1), 1–20.Google Scholar
Freeman, N. C. & Johnson, R. S. 1970 Shallow water waves on shear flows. J. Fluid Mech. 42 (2), 401–409.CrossRefGoogle Scholar
Froude, W. 1874 On Experiments with HMS Greyhound. Institution of Naval Architects.Google Scholar
Groves, M. D. & Wahlén, E. 2007 Spatial dynamics methods for solitary gravity–capillary water waves with an arbitrary distribution of vorticity. SIAM J. Math. Anal. 39 (3), 932–964.Google Scholar
Groves, M. D. & Wahlén, E. 2008 Small-amplitude Stokes and solitary gravity water waves with an arbitrary distribution of vorticity. Physica D 237 (10–12), 1530–1538.Google Scholar
Hur, V. M. 2008a Exact solitary water waves with vorticity. Arch. Rat. Mech. Anal. 188 (2), 213–244.Google Scholar
Hur, V. M. 2008b Symmetry of solitary water waves with vorticity. Math. Res. Lett. 15 (3), 491–509.Google Scholar
Hur, V. M. 2012a Analyticity of rotational flows beneath solitary water waves. Int. Math. Res. Not. IMRN (11), 2550–2570.Google Scholar
Hur, V. M. 2012b No solitary waves exist on 2D deep water. Nonlinearity 25 (12), 3301–3312.CrossRefGoogle Scholar
Hur, V. M. & Lin, Z. 2008 Unstable surface waves in running water. Commun. Math. Phys. 282 (3), 733–796.Google Scholar
Iooss, G.. & Kirchgässner, K. 1990 Bifurcation d’ondes solitaires en présence d’une faible tension superficielle. C. R. Acad. Sci. Paris I 311 (5), 265–268.Google Scholar
Keady, G. & Norbury, J. 1982 Domain comparison theorems for flows with vorticity. Q. J. Mech. Appl. Maths 35 (1), 17–32.Google Scholar
Keady, G. & Pritchard, W. G. 1974 Bounds for surface solitary waves. Proc. Cambridge Philos. Soc. 76, 345–358.Google Scholar
Kozlov, V. & Kuznetsov, N. 2012 Bounds for steady water waves with vorticity. J. Differ. Equ. 252 (1), 663–691.Google Scholar
Kozlov, V. & Kuznetsov, N. 2014 Dispersion equation for water waves with vorticity and Stokes waves on flows with counter-currents. Arch. Rat. Mech. Anal. 214 (3), 971–1018.Google Scholar
Kozlov, V., Kuznetsov, N. & Lokharu, E. 2014 Steady water waves with vorticity: an analysis of the dispersion equation. J. Fluid Mech. 751, R3.Google Scholar
Kozlov, V., Kuznetsov, N. & Lokharu, E. 2015 On bounds and non-existence in the problem of steady waves with vorticity. J. Fluid Mech. 765, R1 (13 pages).Google Scholar
Longuet-Higgins, M. S. 1974 On the mass, momentum, energy and circulation of a solitary wave. Proc. R. Soc. Lond. A 337, 1–13.Google Scholar
Longuet-Higgins, M. S. & Fenton, J. D. 1974 On the mass, momentum, energy and circulation of a solitary wave. II. Proc. R. Soc. Lond. A 340, 471–493.Google Scholar
Longuet-Higgins, M. & Tanaka, M. 1997 On the crest instabilities of steep surface waves. J. Fluid Mech. 336, 51–68.Google Scholar
Martin, C. I. & Matioc, B.-V. 2014 Steady periodic water waves with unbounded vorticity: equivalent formulations and existence results. J. Nonlinear Sci. 24 (4), 633–659.Google Scholar
Matioc, A.-V. & Matioc, B.-V. 2012 Regularity and symmetry properties of rotational solitary water waves. J. Evol. Equ. 12 (2), 481–494.CrossRefGoogle Scholar
McLeod, J. B. 1984 The Froude number for solitary waves. Proc. R. Soc. Edin. A 97, 193–197.Google Scholar
Miles, J. W. 1980 Solitary waves. Annu. Rev. Fluid Mech. 12, 11–43.Google Scholar
Plotnikov, P. I. 1991 Nonuniqueness of solutions of a problem on solitary waves, and bifurcations of critical points of smooth functionals. Izv. Akad. Nauk SSSR Ser. Mat. 55 (2), 339–366.Google Scholar
Starr, V. P. 1947 Momentum and energy integrals for gravity waves of finite height. J. Mar. Res. 6, 175–193.Google Scholar
Sun, S. M. 1999 Non-existence of truly solitary waves in water with small surface tension. Proc. R. Soc. Lond. A 455 (1986), 2191–2228.CrossRefGoogle Scholar
Ter-Krikorov, A. M. 1961 The solitary wave on the surface of a turbulent liquid. Zh. Vychisl. Mat. Mat. Fiz. 1, 1077–1088.Google Scholar
Thompson, P. D. 1949 The propagation of small surface disturbances through rotational flow. Ann. N.Y. Acad. Sci. 51, 463–474.Google Scholar
Toland, J. F. 1996 Stokes waves. Topol. Methods Nonlinear Anal. 7 (1), 1–48.Google Scholar
Vanden-Broeck, J.-M. 1994 Steep solitary waves in water of finite depth with constant vorticity. J. Fluid Mech. 274, 339–348.CrossRefGoogle Scholar
Wahlén, E. 2009 Steady water waves with a critical layer. J. Differ. Equ. 246 (6), 2468–2483.CrossRefGoogle Scholar
Wheeler, M. H. 2013 Large-amplitude solitary water waves with vorticity. SIAM J. Math. Anal. 45 (5), 2937–2994.Google Scholar