Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T08:35:00.936Z Has data issue: false hasContentIssue false
  • English
  • Français

Frontal instabilities and waves in a differentially rotating fluid

Published online by Cambridge University Press:  22 September 2011

J.-B. Flór ,
H. Scolan  and
J. Gula
J.-B. Flór*
Affiliation:
Laboratoire des Écoulements Géophysiques et Industriels, CNRS and Université de Grenoble, BP 53, 38041 Grenoble, France
H. Scolan
Affiliation:
Laboratoire des Écoulements Géophysiques et Industriels, CNRS and Université de Grenoble, BP 53, 38041 Grenoble, France
J. Gula
Affiliation:
Laboratoire de Metéorologie Dynamique, rue Lhomond 75005, Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an experimental investigation of the stability of a baroclinic front in a rotating two-layer salt-stratified fluid. A front is generated by the spin-up of a differentially rotating lid at the fluid surface. In the parameter space set by rotational Froude number, 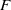, dissipation number, 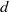(i.e. the ratio between disk rotation time and Ekman spin-down time) and flow Rossby number, a new instability is observed that occurs for Burger numbers larger than the critical Burger number for baroclinic instability. This instability has a much smaller wavelength than the baroclinic instability, and saturates at a relatively small amplitude. The experimental results for the instability regime and the phase speed show overall a reasonable agreement with the numerical results of Gula, Zeitlin & Plougonven (J. Fluid Mech., vol. 638, 2009, pp. 27–47), suggesting that this instability is the Rossby–Kelvin instability that is due to the resonance between Rossby and Kelvin waves. Comparison with the results of Williams, Haines & Read (J. Fluid Mech., vol. 528, 2005, pp. 1–22) and Hart (Geophys. Fluid Dyn., vol. 3, 1972, pp. 181–209) for immiscible fluid layers in a small experimental configuration shows continuity in stability regimes in space, but the baroclinic instability occurs at a higher Burger number than predicted according to linear theory. Small-scale perturbations are observed in almost all regimes, either locally or globally. Their non-zero phase speed with respect to the mean flow, cusped-shaped appearance in the density field and the high values of the Richardson number for the observed wavelengths suggest that these perturbations are in many cases due to Hölmböe instability.

JFM classification

Geophysical and Geological Flows: Baroclinic flows Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 685 , 25 October 2011 , pp. 532 - 542
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: University of Toronto, Department of Physics, Toronto, Canada

References

1. Carpenter, J. R., Balmforth, N. J. & Lawrence, G. A. 2010 Identifying unstable modes in stratified shear layers. Phys. Fluids 22, 054104.CrossRefGoogle Scholar
2. Flór, J.-B. 2007 Frontal instability, inertia-gravity wave radiation and vortex formation. 18 ème congres Francais de Mecanique. Url: http://devirevues.demo.inist.fr/handle/2042/15609.Google Scholar
3. Flór, J.-B., Bush, J. W. M., Bush, M. & Ungarish, 2004 An experimental investigation of spin-up from rest of a stratified fluid. Geophys. Fluid Dyn. 98 (4), 277–296.Google Scholar
4. Ford, R. 1994 Gravity wave radiation from vortex trains in rotating shallow water. J. Fluid Mech. 281, 81–118.Google Scholar
5. Griffiths, R. W. & Linden, P. F. 1981 the stability of buoyancy-driven coastal currents. Dyn. Atmos. Oceans 5 (4), 281–306.Google Scholar
6. Gula, J., Plougonven, R. & Zeitlin, V. 2009a Ageostrophic instabilities of fronts in a channel in a stratified rotating fluid. J. Fluid Mech. 627, 485–507.Google Scholar
7. Gula, J., Zeitlin, V. & Plougonven, R. 2009b Instabilities of two-layer shallow-water flows with vertical shear in the rotating annulus. J. Fluid Mech. 638, 27–47.Google Scholar
8. Hart, J. E. 1972 A laboratory study of baroclinic instability. Geophys. Fluid Dyn. 3, 181–209.Google Scholar
9. Hart, J. E. 1979 Finite amplitude baroclinic instability. Annu. Rev. Fluid Mech. 11, 147–172.Google Scholar
10. Lawrence, G. A., Browand, F. K. & Redekopp, L. G. 1991 The stability of a sheared density interface. Phys. Fluids 3, 2360–2370.Google Scholar
11. Lovegrove, A. F., Read, P. L. & Richards, C. J. 2000 Generation of inertia–gravity waves in a baroclinically unstable fluid. Q. J. R. Meteorol. Soc. 126, 3233–3254.Google Scholar
12. McIntyre, M. E. 2009 Spontaneous imbalance and hybrid vortex–gravity structures. J. Atmos. Sci. 66, 1315–1326.Google Scholar
13. Ortiz, S., Chomaz, J.-M. & Loiseleux, T. 2002 Spatial Hölmböe instability. Phys. Fluids 14, 2585–2597.Google Scholar
14. Pedlosky, J. 2001 Geophysical Fluid Dynamics, 2nd edn. Springer. p. 728.Google Scholar
15. Sakai, S. 1989 Rossby–Kelvin instability: a new type of ageostrophic instability caused by a resonance between Rossby waves and gravity waves. J. Fluid Mech. 202, 149–176.Google Scholar
16. Spence, G. S. M., Foster, M. R. & Davies, P. A. 1992 The transient response of a contained rotating stratified fluid to impulsively started surface forcing. J. Fluid Mech. 243, 33–50.Google Scholar
17. Stegner, A., Bourouet-Aubertot, P. & Pichon, T. 2004 Nonlinear adjustment of density fronts. Part 1. The Rossby scenario and the experimental reality. J. Fluid Mech. 502 (1), 335–360.Google Scholar
18. Williams, P., Haines, T. W. N. & Read, P. L. 2005 On the generation mechanisms of short-scale unbalanced modes in rotating two-layer flows with vertical shear. J. Fluid Mech. 528, 1–22.Google Scholar