Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T07:03:07.918Z Has data issue: false hasContentIssue false
  • English
  • Français

From a steady plume to periodic puffs during confined carbon dioxide dissolution

Published online by Cambridge University Press:  20 September 2018

P. Meunier Open the ORCID record for P. Meunier [Opens in a new window]  and
F. Nadal Open the ORCID record for F. Nadal [Opens in a new window]
P. Meunier
Affiliation:
Aix Marseille Université, Centrale Marseille, CNRS, IRPHE, 13384, Marseille, France
F. Nadal*
Affiliation:
Department of Mechanical, Electrical and Manufacturing Engineering, Loughborough University, LoughboroughLE11 3TU, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, the stability of a laminar plume due to solutal convection is addressed from experimental, numerical and theoretical points of view. A topless vertical tube containing water is put in a pressure cell filled with carbon dioxide (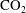$\text{CO}_{2}$). The diffusion of 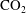$\text{CO}_{2}$ at the free surface creates a thin layer of heavy fluid underneath the surface. This unstable density gradient generates a steady laminar plume which goes downward through the entire tube. A quasi-steady flow settles in the tube, filling gradually the bottom of the tube with heavy fluid. During this laminar regime, the velocity of the plume slowly decreases due to the build-up of the background density gradient. Surprisingly, despite the decrease of the Reynolds number, the laminar plume suddenly destabilises via a varicose mode into periodic pulsed puffs after an onset time which depends on the height of the tube and on the solutal Rayleigh number 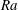$Ra$. This periodic regime is followed by an aperiodic regime, which lasts until the complete saturation of the solution. The observed destabilisation is explained as a result of the interplay between the feedback of the global recirculating flow and the progressive density stratification of the background fluid. The wavelength, frequency, onset time and phase velocity of the instability are explored using particle image velocimetry (PIV) measurements over two decades of Rayleigh number. The characteristics of the instability appear to be almost independent of the Bond number but strongly dependent on the solutal Rayleigh number and the aspect ratio. The phase velocity is very close to the fluid velocity of the plume before the instability, which has been predicted in various works to scale as 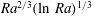$Ra^{2/3}(\ln \,Ra)^{1/3}$. The wavelength is close to 4.5 times the radius of the cylinder (independent of aspect ratio, Bond number and Rayleigh number) such that the frequency scales as the phase velocity. The onset time, which is proportional to the height of the cylinder, scales as 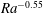$Ra^{-0.55}$ and depends on the Bond number. A simplified model inspired from Lorenz’ waterwheel is proposed to explain the destabilisation process after partial fill-up of the cylinder. Although very qualitative, the model captures the key features of the experimental observations.

JFM classification

Convection: Buoyancy-driven instability Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 1 - 27
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akutsu, T., Yamaji, Y., Yamaguchi, H., Watanabe, M., Smith, R. L. Jr & Inomata, H. 2007 Interfacial tension between water and high-pressure CO2 in the presence of hydrocarbon surfactant. Fluid Phase Equilib. 257, 163–168.Google Scholar
Batchelor, G. K. 1954 Heat convection and buoyancy effects in fluids. Q. J. R. Meteorol. Soc. 80, 339–358.Google Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2006 The route to self-similarity in turbulent jets and plumes. J. Fluid Mech. 547, 137–148.Google Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2010 The rise and fall of turbulent fountains: a new model for improved quantitative predictions. J. Fluid Mech. 657, 265–284.Google Scholar
Cetegen, B. M., Dong, Y. & Soteriou, M. C. 1998 Experiments on stability and oscillatory behaviour of planar buoyant plumes. Phys. Fluids 10, 1658–1665.Google Scholar
Cetegen, B. M. & Kasper, K. D. 1996 Experiments on the oscillatory behavior of buoyant plumes of helium and helium-air mixtures. Phys. Fluids 8 (11), 2974–2984.Google Scholar
Chakravarthy, R. V. K., Lesshafft, L. & Huerre, P. 2015 Local linear stability of laminar axisymmetric plumes. J. Fluid Mech. 780, 344–369.Google Scholar
Chakravarthy, R. V. K., Lesshafft, L. & Huerre, P. 2018 Global stability of buoyant jets and plumes. J. Fluid Mech. 835, 654–673.Google Scholar
Concus, P. 1968 Static menisci in a vertical right cylinder. J. Fluid Mech. 34, 481–495.Google Scholar
Cussler, E. L. 1997 Diffusion: Mass Transfer in Fluid Systems. Cambridge University Press.Google Scholar
Fujii, T. 1963 Theory of the steady laminar natural convection above a horizontal line heat source and a point heat source. Intl J. Heat Mass Transfer 6, 597–606.Google Scholar
Hebach, A., Oberhof, A. & Dahmen, N. 2004 Density of water+carbon dioxide at elevated pressures: measurements and correlation. J. Chem. Engng Data 49 (5), 950–953.Google Scholar
Jiang, X. & Luo, K. H. 2000 Direct numerical simulation of the puffing phenomenon of an axisymmetric thermal plume. Theor. Comput. Fluid Dyn. 14 (1), 55–74.Google Scholar
Kaminski, E., Tait, S. & Carazzo, G. 2005 Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 526, 361–376.Google Scholar
Kimura, S. & Bejan, A. 1983 Mechanism for transition to turbulence in buoyant plume flow. Intl J. Heat Mass Transfer 26 (10), 1515–1532.Google Scholar
Kolář, M. & Gumbs, G. 1992 Theory for the experimental observation of chaos in a rotating waterwheel. Phys. Rev. A 45, 626–637.Google Scholar
Lombardi, M., Caulfield, C. P., Cossu, C., Pesci, A. I. & Goldstein, R. E. 2011 Growth and instability of a laminar plume in a strongly stratified environment. J. Fluid Mech. 671, 184–206.Google Scholar
Lopez, J. M. & Marques, F. 2013 Instability of plumes driven by localized heating. J. Fluid Mech. 736, 616–640.Google Scholar
Maxworthy, T. 1999 The flickering candle: transition to a global oscillation in a thermal plume. J. Fluid Mech. 390, 297–323.Google Scholar
Meunier, P. & Leweke, T. 2003 Analysis and optimization of the error caused by high velocity gradients in particle image velocimetry. Exp. Fluids 35 (5), 408–421.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Nadal, F., Meunier, P., Pouligny, B. & Laurichesse, E. 2013 Stationary plume induced by carbon dioxide dissolution. J. Fluid Mech. 719, 203–229.Google Scholar
Olson, P., Schubert, G. & Anderson, C. 1993 Structure of axisymmetric mantle plumes. J. Geophys. Res. 98, 6829–6844.Google Scholar
Pera, L. & Gebhart, G. 1971 On the stability of laminar plumes: some numerical solutions and experiments. Intl J. Heat Mass Transfer 14, 975–984.Google Scholar
Pesci, A. I., Porter, M. A. & Goldstein, M. A. 2003 Inertially driven buckling and overturning of jets in a Hele-Shaw cell. Phys. Rev. E 68, 056305.Google Scholar
Satti, R. P. & Agrawal, A. K. 2006 Flow structure in the near-field of buoyant low-density gas jets. Intl J. Heat Fluid Flow 27 (2), 336–347.Google Scholar
Soteriou, M. C., Dong, Y. & Cetegen, B. M. 2002 Lagrangian simulation of the unsteady near field dynamics of planar buoyant plumes. Phys. Fluids 14, 3118–3140.Google Scholar
Subbarao, E. R. & Cantwell, B. J. 1992 Investigation of a co-flowing buoyant jet: experiments on the effect of Reynolds number and richardson number. J. Fluid Mech. 245, 69–90.Google Scholar
Torrance, K. E. 1979 Natural convection in thermally stratified enclosures with localized heating from below. J. Fluid Mech. 95 (3), 477–495.Google Scholar
Torrance, K. E., Orloff, L. & Rockett, J. A. 1969 Experiments on natural convection in enclosures with localized heating from below. J. Fluid Mech. 36 (1), 21–31.Google Scholar
Torrance, K. E. & Rockett, J. A. 1969 Numerical study of natural convection in an enclosure with localized heating from below – creeping flow to the onset of laminar instability. J. Fluid Mech. 36 (1), 33–54.Google Scholar
Umemura, A. & Busse, F. H. 1989 Axisymmetric convection at large Rayleigh and infinite Prandtl number. J. Fluid Mech. 208, 459–478.Google Scholar
Vreme, A., Nadal, F., Pouligny, B., Jeandet, P., Liger-Belair, G. & Meunier, P. 2016 Gravitational instability due to the dissolution of carbon dioxide in a hele-shaw cell. Phys. Rev. Fluids 1 (6), 064301.Google Scholar
Whittaker, R. J. & Lister, J. R. 2006a Steady axisymmetric creeping plumes above a planar boundary. Part 1. A point source. J. Fluid Mech. 567, 361–378.Google Scholar
Whittaker, R. J. & Lister, J. R. 2006b Steady axisymmetric creeping plumes above a planar boundary. Part 2. A distributed source. J. Fluid Mech. 567, 379–397.Google Scholar
Williams, T. C., Shaddix, C. R., Schefer, R. W. & Desgroux, P. 2007 The response of buoyant laminar diffusion flames to low-frequency forcing. Combust. Flame 151, 676–684.Google Scholar
Worster, M. G. 1986 The axisymmetric laminar plume: asymptotic solution for large Prandtl number. Stud. Appl. Maths 75, 139–152.Google Scholar
Yang, H. Q. 1992 Buckling of a thermal plume. Intl J. Heat Mass Transfer 35 (6), 1527–1532.Google Scholar
Ybert, C.1998 Stabilisation des mousses aqueuses par des protéines. PhD thesis, Universite Louis Pasteur (Strasbourg I).Google Scholar
Yih, C. S. 1951 Free convection due to a point source of heat. In Proceedings of the First U.S. National Congress of Applied Mechanics, pp. 941–947.Google Scholar

Meunier Supplementary Movie 1

Dynamics of the solutal plume (stages II, III, and IV), observed for the dimensionless parameters $h = 4$, $Ra = 10^6$ and $Bo = 2.2$ (corresponding physical parameters $H = 16$ mm, $R_c = 4$ mm and $P_{\mbox{\scriptsize CO$_2$}} = 6.4$ bar).

Download Meunier Supplementary Movie 1(Video)
Video 15.1 MB
Supplementary material: PDF

Meunier Supplementary Material

Meunier Supplementary Material

Download Meunier Supplementary Material(PDF)
PDF 77.8 KB