Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-05T14:09:56.798Z Has data issue: false hasContentIssue false
  • English
  • Français

Frequency domain and time domain analysis of thermoacoustic oscillations with wave-based acoustics

Published online by Cambridge University Press:  25 June 2015

A. Orchini ,
S. J. Illingworth  and
M. P. Juniper
A. Orchini*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
S. J. Illingworth
Affiliation:
Department of Mechanical Engineering, University of Melbourne, VIC 3010, Australia
M. P. Juniper
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

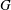Many thermoacoustic systems exhibit rich nonlinear behaviour. Recent studies show that this nonlinear dynamics can be well captured by low-order time domain models that couple a level set kinematic model for a laminar flame, the $G$-equation, with a state-space realization of the linearized acoustic equations. However, so far the 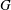$G$-equation has been coupled only with straight ducts with uniform mean acoustic properties, which is a simplistic configuration. In this study, we incorporate a wave-based model of the acoustic network, containing area and temperature variations and frequency-dependent boundary conditions. We cast the linear acoustics into state-space form using a different approach from that in the existing literature. We then use this state-space form to investigate the stability of the thermoacoustic system, both in the frequency and time domains, using the flame position as a control parameter. We observe frequency-locked, quasiperiodic and chaotic oscillations. We identify the location of Neimark–Sacker bifurcations with Floquet theory. We also find the Ruelle–Takens–Newhouse route to chaos with nonlinear time series analysis techniques. We highlight important differences between the nonlinear response predicted by the frequency domain and the time domain methods. This reveals deficiencies with the frequency domain technique, which is commonly used in academic and industrial studies of thermoacoustic systems. We then demonstrate a more accurate approach based on continuation analysis applied to time domain techniques.

JFM classification

Acoustics: Acoustics Nonlinear Dynamical Systems: Low-dimensional models Nonlinear Dynamical Systems: Nonlinear Dynamical Systems
Type
Papers
Information
Journal of Fluid Mechanics , Volume 775 , 25 July 2015 , pp. 387 - 414
Check for updates
Copyright
© The Authors 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Basso, M., Genesio, R. & Tesi, A. 1997 A frequency method for predicting limit cycle bifurcations. Nonlinear Dyn. 13 (4), 339–360.Google Scholar
Bothien, M. R., Moeck, J. P., Lacarelle, A. & Paschereit, C. O. 2007 Time domain modelling and stability analysis of complex thermoacoustic systems. Proc. Inst. Mech. Engrs 221 (5), 657–668.Google Scholar
Chu, B.-T. 1963 Analysis of a self-sustained thermally driven nonlinear vibration. Phys. Fluids 6 (11), 1638–1644.Google Scholar
Creta, F. & Matalon, M. 2011 Strain rate effects on the nonlinear development of hydrodynamically unstable flames. Proc. Combust. Inst. 33 (1), 1087–1094.Google Scholar
Culick, F. E. C. 1971 Non-linear growth and limiting amplitude of acoustic oscillations in combustion chambers. Combust. Sci. Technol. 3 (1), 1–16.Google Scholar
Culick, F. E. C. 1976a Nonlinear behavior of acoustic waves in combustion chambers-I. Acta Astronaut. 3 (9–10), 715–734.Google Scholar
Culick, F. E. C. 1976b Nonlinear behavior of acoustic waves in combustion chambers-II. Acta Astronaut. 3 (9–10), 735–757.Google Scholar
Dowling, A. P. 1997 Nonlinear self-excited oscillations of a ducted flame. J. Fluid Mech. 346, 271–290.Google Scholar
Dowling, A. P. 1999 A kinematic model of a ducted flame. J. Fluid Mech. 394, 51–72.Google Scholar
Dowling, A. P. & Stow, S. R. 2003 Acoustic analysis of gas turbine combustors. J. Propul. Power 19 (5), 751–764.Google Scholar
Eldredge, J. D. & Dowling, A. P. 2003 The absorption of axial acoustic waves by a perforated liner with bias flow. J. Fluid Mech. 485, 307–335.Google Scholar
Evesque, S., Dowling, A. P. & Annaswamy, A. M. 2003 Self-tuning regulators for combustion oscillations. Proc. R. Soc. Lond. A 459 (2035), 1709–1749.Google Scholar
Gotoda, H., Nikimoto, H., Miyano, T. & Tachibana, S. 2011 Dynamic properties of combustion instability in a lean premixed gas-turbine combustor. Chaos 21 (1), 013124.Google Scholar
Gotoda, H., Shinoda, Y., Kobayashi, M., Okuno, Y. & Tachibana, S. 2014 Detection and control of combustion instability based on the concept of dynamical system theory. Phys. Rev. E 89, 022910.Google Scholar
Guckenheimer, J. & Holmes, P. 1983 Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer.Google Scholar
Heckl, M. A. 1988 Active control of the noise from a Rijke tube. J. Sound Vib. 124 (1), 117–133.CrossRefGoogle Scholar
Heckl, M. A. 1990 Non-linear acoustic effects in the Rijke tube. Acustica 72, 63–71.Google Scholar
Heckl, M. A. & Howe, M. S. 2007 Stability analysis of the Rijke tube with a Green’s function approach. J. Sound Vib. 305 (4–5), 672–688.Google Scholar
Hemchandra, S.2009 Dynamics of turbulent premixed flames in acoustic fields. PhD thesis, Georgia Institute of Technology.Google Scholar
Illingworth, S. J. & Juniper, M. P.2014 Acoustic state-space model using a wave-based approach. In 21st International Congress on Sound and Vibration, 13–17 July 2014, Beijing, China (ed. M. J. Crocker). IIAV.Google Scholar
Kabiraj, L., Saurabh, A., Wahi, P. & Sujith, R. I. 2012a Route to chaos for combustion instability in ducted laminar premixed flames. Chaos 22 (2), 023129.Google Scholar
Kabiraj, L. & Sujith, R. I. 2012 Nonlinear self-excited thermoacoustic oscillations: intermittency and flame blowout. J. Fluid Mech. 713, 376–397.Google Scholar
Kabiraj, L., Sujith, R. I. & Wahi, P. 2012b Bifurcations of self-excited ducted laminar premixed flames. J. Engng Gas Turbines Power 134 (3), 031502.Google Scholar
Kantz, H. & Schreiber, T. 2004 Nonlinear Time Series Analysis, 2nd edn. Cambridge University Press.Google Scholar
Karimi, N., Brear, M. J., Jin, S.-H. & Monty, J. P. 2009 Linear and non-linear forced response of a conical, ducted, laminar premixed flame. Combust. Flame 156 (11), 2201–2212.Google Scholar
Kashinath, K., Hemchandra, S. & Juniper, M. P. 2013a Nonlinear phenomena in thermoacoustic systems with premixed flames. J. Engng Gas Turbines Power 135 (6), 061502.Google Scholar
Kashinath, K., Hemchandra, S. & Juniper, M. P. 2013b Nonlinear thermoacoustics of ducted premixed flames: the influence of perturbation convection speed. Combust. Flame 160 (12), 2856–2865.Google Scholar
Kashinath, K., Waugh, I. C. & Juniper, M. P. 2014 Nonlinear self-excited thermoacoustic oscillations of a ducted premixed flame: bifurcations and routes to chaos. J. Fluid Mech. 761, 399–430.Google Scholar
Khalil, H. K. 2001 Nonlinear Systems, 3rd edn. Prentice Hall.Google Scholar
Lang, W., Poinsot, T. & Candel, S. 1987 Active control of combustion instability. Combust. Flame 70, 281–289.Google Scholar
Lieuwen, T. C. 2012 Unsteady Combustor Physics. Cambridge University Press.Google Scholar
Mangesius, H. & Polifke, W. 2011 A discrete-time, state-space approach for the investigation of non-normal effects in thermoacoustic systems. Intl J. Spray Combust. Dyn. 3 (4), 331–350.Google Scholar
Markstein, G. H. 1964 Non-Steady Flame Propagation. Pergamon.Google Scholar
Matveev, K. I. 2003 Energy consideration of the nonlinear effects in a Rijke tube. J. Fluids Struct. 18, 783–794.Google Scholar
Moeck, J. P. & Paschereit, C. O. 2012 Nonlinear interactions of multiple linearly unstable thermoacoustic modes. Intl J. Spray Combust. Dyn. 4, 1–28.Google Scholar
Nicoud, F., Benoit, L., Sensiau, C. & Poinsot, T. 2007 Acoustic modes in combustors with complex impedances and multidimensional active flames. AIAA J. 45 (2), 426–441.Google Scholar
Noiray, N., Durox, D., Schuller, T. & Candel, S. 2008 A unified framework for nonlinear combustion instability analysis based on the flame describing function. J. Fluid Mech. 615, 139–167.Google Scholar
Peng, D., Merriman, B., Osher, S., Zhao, H. & Kang, M. 1999 A PDE-based fast local level set method. J. Comput. Phys. 155 (2), 410–438.Google Scholar
Preetham, Santosh, H & Lieuwen, T. 2008 Dynamics of laminar premixed flames forced by harmonic velocity disturbances. J. Propul. Power 24 (6), 1390–1402.CrossRefGoogle Scholar
Saad, Y. & Schultz, M. H. 1986 GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7 (3), 856–869.Google Scholar
Schmid, M., Blumenthal, R. S., Schulze, M., Polifke, W. & Sattelmayer, T. 2013 Quantitative stability analysis using real-valued frequency response data (GT2013-95945). J. Eng. Gas Turbines Power 135 (12), 121601.Google Scholar
Schuermans, B.2003 Modeling and control of thermoacoustic instabilities. PhD thesis, Ecole Polytechnique Fédérale de Lausanne.Google Scholar
Schuller, T., Durox, D. & Candel, S. 2003 A unified model for the prediction of laminar flame transfer functions: comparisons between conical and V-flames dynamics. Combust. Flame 134 (1–2), 21–34.Google Scholar
Sethian, J. A. 1999 Level Set Methods and Fast Marching Methods, 2nd edn. Cambridge University Press.Google Scholar
Shreekrishna, H. S. & Lieuwen, T. 2010 Laminar premixed flame response to equivalence ratio oscillations. Combust. Theor. Model. 14 (5), 681–714.Google Scholar
Stow, S. R. & Dowling, A. P.2001 Proceedings of ASME Turbo Expo, New Orleans, LA, 4–7 June 2001 (GT2001-0037). American Society of Mechanical Engineers; Thermoacoustic oscillations in an annular combustor.Google Scholar
Stow, S. R. & Dowling, A. P. 2004 Techincal Paper GT2004-54245. American Society of Mechanical Engineers; Low-order modelling of thermoacoustic limit cycles.Google Scholar
Subramanian, P., Mariappan, S., Sujith, R. I. & Wahi, P. 2010 Bifurcation analysis of thermoacoustic instability in a horizontal Rijke tube. Intl J. Spray Combust. Dyn. 2 (4), 325–356.Google Scholar
Thompson, J. M. T. & Stewart, H. B. 2001 Nonlinear Dynamics and Chaos, 2nd edn. Wiley.Google Scholar
Waugh, I., Illingworth, S. & Juniper, M. 2013 Matrix-free continuation of limit cycles for bifurcation analysis of large thermoacoustic systems. J. Comput. Phys. 240, 225–247.Google Scholar
Waugh, I. C., Kashinath, K. & Juniper, M. P. 2014 Matrix-free continuation of limit cycles and their bifurcations for a ducted premixed flame. J. Fluid Mech. 759, 1–27.Google Scholar
Yang, V., Kim, S. I. & Culick, F. E. C. 1990 Triggering of longitudinal pressure oscillations in combustion chambers. I: nonlinear gasdynamics. Combust. Sci. Technol. 72, 183–214.Google Scholar
Zinn, B. T. & Lores, M. E. 1971 Application of the Galerkin method in the solution of non-linear axial combustion instability problems in liquid rockets. Combust. Sci. Technol. 4 (1), 269–278.Google Scholar