Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Derakhshandeh, J.F.
and
Alam, Md Mahbub
2019.
A review of bluff body wakes.
Ocean Engineering,
Vol. 182,
Issue. ,
p.
475.
Chen, Weilin
Ji, Chunning
Xu, Dong
and
Zhang, Zhimeng
2020.
Oscillation regimes and mechanisms in the vortex-induced vibrations of three circular cylinders with equilateral-triangular arrangements.
Physics of Fluids,
Vol. 32,
Issue. 4,
Ding, Chenwei
Srinil, Narakorn
Bao, Yan
Zhou, Dai
and
Han, Zhaolong
2020.
Vortex-induced vibrations of two mechanically coupled circular cylinders with asymmetrical stiffness in side-by-side arrangements.
Journal of Fluids and Structures,
Vol. 95,
Issue. ,
p.
102995.
Albuquerque, Daniel P.
Sandberg, Mats
Linden, P.F.
and
Carrilho da Graça, Guilherme
2020.
Experimental and numerical investigation of pumping ventilation on the leeward side of a cubic building.
Building and Environment,
Vol. 179,
Issue. ,
p.
106897.
Lee, Yin Jen
Zhou, Guangya
and
Lua, Kim Boon
2020.
Mass ratio definition of vortex-induced vibration systems with added mass consideration.
Engineering Research Express,
Vol. 2,
Issue. 4,
p.
045007.
Chen, Zhenlin
Alam, Md. Mahbub
Qin, Bin
and
Zhou, Yu
2020.
Energy harvesting from and vibration response of different diameter cylinders.
Applied Energy,
Vol. 278,
Issue. ,
p.
115737.
Chen, Wen-Li
Yang, Wen-Han
Xu, Feng
and
Zhang, Chen-Guang
2020.
Complex wake-induced vibration of aligned hangers behind tower of long-span suspension bridge.
Journal of Fluids and Structures,
Vol. 92,
Issue. ,
p.
102829.
Yuan, Wenyong
Sun, Hai
Li, Hui
and
Bernitsas, Michael M.
2020.
Flow-induced oscillation patterns for two tandem cylinders with turbulence stimulation and variable stiffness and damping.
Ocean Engineering,
Vol. 218,
Issue. ,
p.
108237.
Hua, Xugang
Wang, Chaoqun
Li, Shengli
and
Chen, Zhengqing
2020.
Experimental investigation of wind-induced vibrations of main cables for suspension bridges in construction phases.
Journal of Fluids and Structures,
Vol. 93,
Issue. ,
p.
102846.
Fan, Xiantao
Wang, Zhongchen
Chen, Xiaoyu
Wang, Yang
and
Tan, Wei
2020.
Experimental investigation on flow-induced vibration of flexible multi cylinders in atmospheric boundary layer.
International Journal of Mechanical Sciences,
Vol. 183,
Issue. ,
p.
105815.
Zhu, Hongjun
Tan, Xiaonian
Gao, Yun
Zhou, Tongming
and
Liu, Wenli
2020.
Two-degree-of-freedom flow-induced vibration of two rigidly coupled tandem cylinders of unequal diameters.
Ocean Engineering,
Vol. 216,
Issue. ,
p.
108142.
Fukushima, Haruki
Yagi, Tomomi
Shimoda, Takuya
and
Noguchi, Kyohei
2021.
Wake-induced instabilities of parallel circular cylinders with tandem and staggered arrangements.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 215,
Issue. ,
p.
104697.
Alam, Md. Mahbub
Chao, Li-Ming
Rehman, Shafiqur
Ji, Chunning
and
Wang, Hanfeng
2021.
Energy harvesting from passive oscillation of inverted foil.
Physics of Fluids,
Vol. 33,
Issue. 7,
Fan, Xiantao
Wang, Zhongchen
Wang, Yang
and
Tan, Wei
2021.
The effect of vortices structures on the flow-induced vibration of three flexible tandem cylinders.
International Journal of Mechanical Sciences,
Vol. 192,
Issue. ,
p.
106132.
Alam, Md. Mahbub
2021.
Effects of Mass and Damping on Flow-Induced Vibration of a Cylinder Interacting with the Wake of Another Cylinder at High Reduced Velocities.
Energies,
Vol. 14,
Issue. 16,
p.
5148.
Sun, Xu
Li, Shuai
Lin, Gang-Gui
and
Zhang, Jia-Zhong
2021.
Effects of flow-induced vibration on forced convection heat transfer from two tandem circular cylinders in laminar flow.
International Journal of Mechanical Sciences,
Vol. 195,
Issue. ,
p.
106238.
Soares, Bruno
and
Srinil, Narakorn
2021.
Modelling of wake-induced vibrations of tandem cylinders with a nonlinear wake-deficit oscillator.
Journal of Fluids and Structures,
Vol. 105,
Issue. ,
p.
103340.
Rastan, M. R.
and
Alam, Md. Mahbub
2021.
Transition of wake flows past two circular or square cylinders in tandem.
Physics of Fluids,
Vol. 33,
Issue. 8,
Ping, Huan
Zhu, Hongbo
Zhang, Kai
Zhou, Dai
Bao, Yan
and
Han, Zhaolong
2021.
Vortex-induced vibrations of two rigidly coupled circular cylinders of unequal diameters at low Reynolds number.
Physics of Fluids,
Vol. 33,
Issue. 10,
Ma, Bowen
Srinil, Narakorn
Zhu, Hongjun
and
Gao, Yue
2021.
Experimental Measurement of Large-Amplitude Intermittent Vibrations of an Inclined Bendable Riser Transporting Unsteady Multiphase Flows.
Applied Ocean Research,
Vol. 113,
Issue. ,
p.
102731.
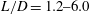 $L/D=1.2{-}6.0$ and reduced velocity
$L/D=1.2{-}6.0$ and reduced velocity 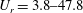 $U_{r}=3.8{-}47.8$, where
$U_{r}=3.8{-}47.8$, where 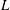 $L$ is the cylinder centre-to-centre spacing and
$L$ is the cylinder centre-to-centre spacing and 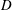 $D$ is the cylinder diameter. Both cylinders are allowed to vibrate only laterally. Extensive measurements are conducted to capture the cylinder vibration and frequency responses, surface pressures, shedding frequencies and flow fields using laser vibrometer, hotwire, pressure scanner and PIV techniques. Four vibration regimes are identified based on the characteristics and generation mechanisms of the cylinder galloping vibrations. Several findings are made on the mechanisms of vibration generation and sustainability. First, the initial states (vibrating or fixed) of a cylinder may have a pronounced impact on the vibration of the other. Second, alternating reattachment, detachment, rolling up and shedding of the upper and lower gap shear layers all contribute to the vibrations. Third, the gap vortices around the base surface of the upstream cylinder produce positive work on the cylinder, sustaining the upstream cylinder vibration. Fourth, reattachment, detachment and switching of the gap shear layers result in largely positive work on the downstream cylinder, playing an important role in sustaining its vibration.
$D$ is the cylinder diameter. Both cylinders are allowed to vibrate only laterally. Extensive measurements are conducted to capture the cylinder vibration and frequency responses, surface pressures, shedding frequencies and flow fields using laser vibrometer, hotwire, pressure scanner and PIV techniques. Four vibration regimes are identified based on the characteristics and generation mechanisms of the cylinder galloping vibrations. Several findings are made on the mechanisms of vibration generation and sustainability. First, the initial states (vibrating or fixed) of a cylinder may have a pronounced impact on the vibration of the other. Second, alternating reattachment, detachment, rolling up and shedding of the upper and lower gap shear layers all contribute to the vibrations. Third, the gap vortices around the base surface of the upstream cylinder produce positive work on the cylinder, sustaining the upstream cylinder vibration. Fourth, reattachment, detachment and switching of the gap shear layers result in largely positive work on the downstream cylinder, playing an important role in sustaining its vibration.

