Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-19T16:07:08.361Z Has data issue: false hasContentIssue false
  • English
  • Français

Formation and interaction of multiple secondary flow vortical structures in a curved pipe: transient and oscillatory flows

Published online by Cambridge University Press:  01 August 2019

Mohammad Reza Najjari Open the ORCID record for Mohammad Reza Najjari [Opens in a new window] ,
Christopher Cox Open the ORCID record for Christopher Cox [Opens in a new window]  and
Michael W. Plesniak Open the ORCID record for Michael W. Plesniak [Opens in a new window]
Mohammad Reza Najjari
Affiliation:
Biofluid Dynamics Laboratory, Department of Mechanical and Aerospace Engineering, The George Washington University, 800 22nd Street NW, Washington, DC 20052, USA
Christopher Cox
Affiliation:
Biofluid Dynamics Laboratory, Department of Mechanical and Aerospace Engineering, The George Washington University, 800 22nd Street NW, Washington, DC 20052, USA
Michael W. Plesniak*
Affiliation:
Biofluid Dynamics Laboratory, Department of Mechanical and Aerospace Engineering, The George Washington University, 800 22nd Street NW, Washington, DC 20052, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Transient, steady and oscillatory flows in a 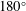$180^{\circ }$ curved pipe are investigated both numerically and experimentally to understand secondary flow vortex formation and interactions. The results of numerical simulations and particle image velocimetry experiments are highly correlated, with a low error. To enable simulations in a smaller domain with shorter inlet section, an analytical solution for the unsteady Navier–Stokes equation is obtained with non-zero initial conditions to provide physical velocity profiles for the simulations. The vorticity transport equation is studied and its terms are balanced to find the mechanism of vorticity transfer to structures in the curved pipe. Several vortices are identified via various vortex identification (ID) methods and their results are compared. Isosurfaces of the 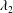$\unicode[STIX]{x1D706}_{2}$ vortex ID are used to explain the temporal and spatial evolution of vortices in the curved pipe. Eigenvalues and eigenvectors of the velocity gradient tensor are calculated for the swirling strength vortex ID method, which also determines vortex axis orientation. The classical Lyne vortex in oscillatory flow with an inviscid core is also revisited and its results are compared with the transient and steady flows. These in-depth analyses provide a better understanding and characterization of vortical structures in the curved pipe flow. Our findings show that, although there are some visual similarities between cross-sectional views of steady/transient flows and oscillatory flows, the structure herein designated as Lyne-type vortex detected in the cross-sections (under steady, transient and pulsatile flows) is not the same as the classical Lyne vortex pair (in oscillatory flows).

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex interactions Biological Fluid Dynamics: Biomedical flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , pp. 481 - 526
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alastruey, J., Siggers, J. H., Peiffer, V., Doorly, D. J. & Sherwin, S. J. 2012 Reducing the data: analysis of the role of vascular geometry on blood flow patterns in curved vessels. Phys. Fluids 24 (3), 31902.Google Scholar
Berger, S. A., Talbot, L. & Yao, L.-S. 1983 Flow in curved pipes. Annu. Rev. Fluid Mech. 15, 461–512.Google Scholar
Boiron, O., Deplano, V. & Pelissier, R. 2007 Experimental and numerical studies on the starting effect on the secondary flow in a bend. J. Fluid Mech. 574, 109–129.Google Scholar
Boshier, F. A. T. & Mestel, A. J. 2017 Complex solutions of the Dean equations and non-uniqueness at all Reynolds numbers. J. Fluid Mech. 818, 241–259.Google Scholar
Boutabaa, M., Helin, L., Mompean, G. & Thais, L. 2009 Numerical study of Dean vortices in developing Newtonian and viscoelastic flows through a curved duct of square cross-section. C. R. Méc. 337 (1), 40–47.Google Scholar
Canton, J., Örlü, R. & Schlatter, P. 2017 Characterisation of the steady, laminar incompressible flow in toroidal pipes covering the entire curvature range. Intl J. Heat Fluid Flow 66, 95–107.Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Cox, C.2017 Development of a high-order Navier–Stokes solver using flux reconstruction to simulate three-dimensional vortex structures in a curved artery model. PhD thesis, The George Washington University.Google Scholar
Das, D. & Arakeri, J. H. 1998 Transition of unsteady velocity profiles with reverse flow. J. Fluid Mech. 374, 251–283.Google Scholar
Das, D. & Arakeri, J. H. 2000 Unsteady laminar duct flow with a given volume flow rate variation. Trans. ASME J. Appl. Mech. 67 (2), 274–281.Google Scholar
Dean, W. R. 1927a Note on the motion of fluid in a curved pipe. Lond. Edinb. Dublin Phil. Mag. J. Sci. 4 (20), 208–223.Google Scholar
Dean, W. R. 1927b The stream-line motion of fluid in a curved pipe. Lond. Edinb. Dublin Phil. Mag. J. Sci. 5 (30), 673–695.Google Scholar
Glenn, A. L., Bulusu, K. V., Shu, F. & Plesniak, M. W. 2012 Secondary flow structures under stent-induced perturbations for cardiovascular flow in a curved artery model. Intl J. Heat Fluid Flow 35, 76–83.Google Scholar
Hamakiotes, C. C. & Berger, S. A. 1988 Fully developed pulsatile flow in a curved pipe. J. Fluid Mech. 195, 23–55.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the 1988 Summer Program of the Center for Turbulence Research, pp. 193–207. NASA Ames/Stanford University.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Krishna, C. V., Gundiah, N. & Arakeri, J. H. 2017 Separations and secondary structures due to unsteady flow in a curved pipe. J. Fluid Mech. 815, 26–59.Google Scholar
Lyne, W. H. 1971 Unsteady viscous flow in a curved pipe. J. Fluid Mech. 45 (01), 13–32.Google Scholar
Morton, B. R. 1984 The generation and decay of vorticity. Geophys. Astrophys. Fluid Dyn. 28 (3–4), 277–308.Google Scholar
Najjari, M. R.2019 On the formation of vortices under transient and pulsatile inflow conditions in a curved pipe. PhD thesis, The George Washington University.Google Scholar
Najjari, M. R., Hinke, J. A., Bulusu, K. V. & Plesniak, M. W. 2016 On the rheology of refractive-index-matched, non-Newtonian blood-analog fluids for PIV experiments. Exp. Fluids 57 (6), 1–6.Google Scholar
Najjari, M. R. & Plesniak, M. W. 2016 Evolution of vortical structures in a curved artery model with non-Newtonian blood-analog fluid under pulsatile inflow conditions. Exp. Fluids 57 (6), 1–16.Google Scholar
Najjari, M. R. & Plesniak, M. W. 2017 PID controller design to generate pulsatile flow rate for in vitro experimental studies of physiological flows. Biomed. Engng Lett. 7 (4), 339–344.Google Scholar
Najjari, M. R. & Plesniak, M. W. 2019 Secondary flow vortical structures in a 180° elastic curved vessel with torsion under steady and pulsatile inflow conditions. Phys. Rev. Fluids 3 (1), 013101.Google Scholar
Siggers, J. H. & Waters, S. L. 2008 Unsteady flows in pipes with finite curvature. J. Fluid Mech. 600, 133–165.Google Scholar
Sudo, K., Sumida, M. & Yamane, R. 1992 Secondary motion of fully developed oscillatory flow in a curved pipe. J. Fluid Mech. 237, 189–208.Google Scholar
Tada, S., Oshima, S. & Yamane, R. 1996 Classification of pulsating flow patterns in curved pipes. Trans. ASME J. Biomech. Engng 118 (3), 311–317.Google Scholar
Vollmers, H. 2001 Detection of vortices and quantitative evaluation of their main parameters from experimental velocity data. Meas. Sci. Technol. 12 (8), 1199–1207.Google Scholar
van Wyk, S., Prahl Wittberg, L., Bulusu, K. V., Fuchs, L. & Plesniak, M. W. 2015 Non-Newtonian perspectives on pulsatile blood-analog flows in a 180° curved artery model. Phys. Fluids 27 (7), 071901.Google Scholar
Yuki, K., Hasegawa, S., Sato, T., Hashizume, H., Aizawa, K. & Yamano, H. 2011 Matched refractive-index PIV visualization of complex flow structure in a three-dimensionally connected dual elbow. Nucl. Engng Des. 241 (11), 4544–4550.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar

Najjari et al. supplementary movie 1

Vorticity component normal to each plane for Moderate-Step flow rate with no-slip wall condition. Four cross-sectional slices are shown at the 30○, 45○, 60○, and 90○ locations and the axial slice location is at the Z=-2.5 mm. The black line in the cross-sectional views shows the location of axial slice. Vorticity component along Z direction (shown in axial slice) forms a branch at t≈0.24 between 30○ and 60○ cross-sections closer to inner wall which this vorticity region is connected to the Lyne-type vortex region later in time.

Download Najjari et al. supplementary movie 1(Video)
Video 8.6 MB

Najjari et al. supplementary movie 2

Vorticity component normal to each plane for Moderate-Step flow rate with idealized slip wall condition. Four cross-sectional slices are shown at the 30○, 45○, 60○, and 90○ locations and the axial slice location is at the Z=-2.5 mm. The black line in the cross-sectional views shows the location of axial slice. Vorticity component along Z direction (shown in axial slice) which is introduced by inlet velocity profile propagates through the curved pipe and forms the Lyne-type vortex region later in time.

Download Najjari et al. supplementary movie 2(Video)
Video 18.5 MB

Najjari et al. supplementary movie 3

Iso-surface of λ2=-90, colored by streamwise vorticity (ωn) component for the Moderate-Step flow rate with no-slip wall condition at four instances in time. ωn vorticity shown at the 90○ cross-section and the shaded areas are corresponding to λ2≤-90 locations identifying vortex core. This figure shows the formation phase of Lyne-Type vortex.

Download Najjari et al. supplementary movie 3(Video)
Video 8 MB

Najjari et al. supplementary movie 4

Iso-surface of λ2=-40, colored by streamwise vorticity (ωn) component for the Moderate-Step flow rate with slip wall condition at four instances in time. ωn vorticity shown at the 90○ cross-section and the shaded areas are corresponding to λ2≤-40 locations identifying vortex core.

Download Najjari et al. supplementary movie 4(Video)
Video 14.9 MB

Najjari et al. supplementary movie 5

Contours of λ2<0 at the 55○ cross-section during the High-Step transient flow. This figure shows that only the deformed-Dean (DD) vortices existed at the beginning of the flow and later in time at t=0.135 s the Lyne-type (LT) vortex is forming, while at later times toward the steady state condition λ2 shows a connected regions of three vortices (in dark blue).

Download Najjari et al. supplementary movie 5(Video)
Video 11.5 MB

Najjari et al. supplementary movie 6

Streamwise vorticity (ωn) contour and secondary velocity streamlines at the 90○ cross-section of the pipe during pure oscillatory flow in Lyne problem with $\alpha=17$ and maximum Re=700. The axial (streamwise) velocity profile is plotted along the horizontal diameter (black) line in cross-section, and ωn is plotted along the vertical radius (blue line). The labels DD and L denote the deformed-Dean and Lyne vortices, respectively.

Download Najjari et al. supplementary movie 6(Video)
Video 14 MB

Najjari et al. supplementary movie 7

Three-dimensional and side views of vortex regions identified by swirling strength (λci>0) at the 90○ cross-section during the oscillatory sinusodal flow rate. Plotted lines (ξn) are parallel to the vortex axis and show the rotation axis. The ξn lines are colored by ωn and show that the Lyne vortex is mostly aligned with the streamwise direction. The lower half of pipes wall are shown to illustrate the angle of view.

Download Najjari et al. supplementary movie 7(Video)
Video 19.4 MB