Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-26T15:48:37.211Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid viscoelasticity affects ultrasound force field-induced particle transport

Published online by Cambridge University Press:  28 November 2024

T. Sujith Open the ORCID record for T. Sujith [Opens in a new window] ,
L. Malik Open the ORCID record for L. Malik [Opens in a new window]  and
A.K. Sen Open the ORCID record for A.K. Sen [Opens in a new window]
T. Sujith
Affiliation:
Micro Nano Bio Fluidics Unit, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
L. Malik
Affiliation:
Micro Nano Bio Fluidics Unit, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
A.K. Sen*
Affiliation:
Micro Nano Bio Fluidics Unit, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

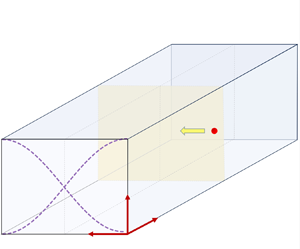
Ultrasonic standing wave technology offers an ideal platform for manipulating particles in microfluidics. We study how fluid viscoelasticity and acoustic boundary formation in micro-confinements affect ultrasound-induced perturbations. These perturbations influence acoustic energy density (AED) and consequently particle transport dynamics. Our approach combines theoretical, numerical and experimental methods. Using the Oldroyd-B model for viscoelastic fluids, we advance acoustic radiation force (ARF) formulations of Doinikov et al. (Phys. Rev. E, vol. 104, no. 6, 2021a; Phys. Rev. E, vol. 104, no. 6, 2021b) for particles much smaller than the acoustic wavelength. This improved approach allows us to decouple AED and acoustic contrast factor terms in the ARF expression. It also enables us to examine the effects of viscoelastic parameters: $\mu ^*$ (ratio of the viscosity of the viscoelastic fluid to that of base Newtonian fluid) and $De$ (product of fluid relaxation time and actuation frequency) on AED and particle migration. Remarkably, we show that increasing fluid elasticity or $De$ transitions viscoelastic fluids from the energy dissipation (relaxation) mode to the energy storage (frozen) mode, increasing AED. Conversely, increasing viscosity ($\mu ^*$) reduces AED. Thus, our findings suggest that elastic effects accelerate particle migration, while viscous effects decelerate it. Consequently, a viscoelastic fluid-filled micro-confinement acts as an energy dissipation device at low $De$ and an energy storage device at high $De$. Particle migration can be controlled by adjusting viscoelastic and acoustic parameters, at a fixed power input. Our theoretical and numerical findings are validated with our experimental data. Our study advances the fundamental understanding of particle migration in viscoelastic fluids under ultrasound, and can significantly impact future studies on particle/cell migration in bio-fluids.

JFM classification

Micro-/Nano-fluid dynamics: Microscale transport Non-Newtonian Flows: Viscoelasticity Waves/Free-surface Flows: Shear waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A75
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Allegra, J.R. & Hawley, S.A. 1972 Attenuation of sound in suspensions and emulsions: theory and experiments. J. Acoust. Soc. Am. 51 (5B), 1545–1564.CrossRefGoogle Scholar
Baasch, T. & Dual, J. 2018 Acoustofluidic particle dynamics: beyond the Rayleigh limit. J. Acoust. Soc. Am. 143, 509–519.CrossRefGoogle ScholarPubMed
Baasch, T., Pavlic, A. & Dual, J. 2019 Acoustic radiation force acting on a heavy particle in a standing wave can be dominated by the acoustic microstreaming. Phys. Rev. E 100 (6), 061102(R).CrossRefGoogle Scholar
Bach, J.S. & Bruus, H. 2018 Theory of pressure acoustics with viscous boundary layers and streaming in curved elastic cavities. J. Acoust. Soc. Am. 144 (2), 766–784.CrossRefGoogle ScholarPubMed
Barnkob, R., Augustsson, P., Laurell, T. & Bruus, H. 2010 Measuring the local pressure amplitude in microchannel acoustophoresis. Lab on a Chip 10 (5), 563–570.CrossRefGoogle ScholarPubMed
Bird, R.R., Armstrong, R.C. & Hassager, O. 1977 Dynamics of Polymeric Liquids, Volume 1: Fluid Mechanics. Wiley.Google Scholar
Brown, J.W. & Churchill, R.V. 2009 Complex Variables and Applications. McGraw-Hill.Google Scholar
Brust, M., Schaefer, C., Doerr, R., Pan, L., Garcia, M., Arratia, P.E. & Wagner, C. 2013 Rheology of human blood plasma: viscoelastic versus newtonian behavior. Phys. Rev. Lett. 110 (7), 078305.CrossRefGoogle ScholarPubMed
Bruus, H. 2012 a Acoustofluidics 2: perturbation theory and ultrasound resonance modes. Lab on a Chip 12 (1), 20–28.CrossRefGoogle ScholarPubMed
Bruus, H. 2012 b Acoustofluidics 7: the acoustic radiation force on small particles. Lab on a Chip 12 (6), 1014.CrossRefGoogle ScholarPubMed
Challis, R.E., Povey, M.J.W., Mather, M.L. & Holmes, A.K. 2005 Ultrasound techniques for characterizing colloidal dispersions. Rep. Prog. Phys. 68 (7), 1541–1637.CrossRefGoogle Scholar
Chaudhuri, O., Cooper-White, J., Janmey, P.A., Mooney, D.J. & Shenoy, V.B. 2020 Effects of extracellular matrix viscoelasticity on cellular behaviour. Nature 584 (7822), 535–546.CrossRefGoogle ScholarPubMed
Chien, S. 1970 Shear dependence of effective cell volume as a determinant of blood viscosity. Science 168 (3934), 977–979.CrossRefGoogle ScholarPubMed
D'Avino, G., Greco, F. & Maffettone, P.L. 2017 Particle migration due to viscoelasticity of the suspending liquid and its relevance in microfluidic devices. Annu. Rev. Fluid Mech. 49, 341–360.CrossRefGoogle Scholar
Doinikov, A.A. 1997 Acoustic radiation force on a spherical particle in a viscous heat-conducting fluid. II. Force on a rigid sphere. J. Acoust. Soc. Am. 101 (2), 722–730.CrossRefGoogle Scholar
Doinikov, A.A., Fankhauser, J. & Dual, J. 2021 a Nonlinear dynamics of a solid particle in an acoustically excited viscoelastic fluid. I. Acoustic streaming. Phys. Rev. E 104 (6), 065107.Google Scholar
Doinikov, A.A., Fankhauser, J. & Dual, J. 2021 b Nonlinear dynamics of a solid particle in an acoustically excited viscoelastic fluid. II. Acoustic radiation force. Phys. Rev. E 104 (6), 065108.Google Scholar
Dual, J. & Möller, D. 2012 Acoustofluidics 4: piezoelectricity and application in the excitation of acoustic fields for ultrasonic particle manipulation. Lab on a Chip 12 (3), 506.CrossRefGoogle ScholarPubMed
Dual, J. & Schwarz, T. 2012 Acoustofluidics 3: continuum mechanics for ultrasonic particle manipulation. Lab on a Chip 12 (2), 244–252.CrossRefGoogle ScholarPubMed
Ebagninin, K.W., Benchabane, A. & Bekkour, K. 2009 Rheological characterization of poly(ethylene oxide) solutions of different molecular weights. J. Colloid Interface Sci. 336 (1), 360–367.CrossRefGoogle ScholarPubMed
Faroughi, S.A., Fernandes, C., Miguel Nóbrega, J. & McKinley, G.H. 2020 A closure model for the drag coefficient of a sphere translating in a viscoelastic fluid. J. Non-Newtonian Fluid Mech. 277, 104218.CrossRefGoogle Scholar
Gorkov, L.P. 1962 On the forces acting on a small particle in an acoustical field in an ideal fluid. Sov. Phys. Dokl. 6, 773.Google Scholar
Hahn, P., Leibacher, I., Baasch, T. & Dual, J. 2015 Numerical simulation of acoustofluidic manipulation by radiation forces and acoustic streaming for complex particles. Lab on a Chip 15 (22), 4302–4313.CrossRefGoogle ScholarPubMed
Hamilton, M.F., Ilinskii, Y.A. & Zabolotskaya, E.A. 2003 Acoustic streaming generated by standing waves in two-dimensional channels of arbitrary width. J. Acoust. Soc. Am. 113 (1), 153–160.CrossRefGoogle ScholarPubMed
Hazra, S., Nath, A., Mitra, S.K. & Sen, A.K. 2021 Dynamics of rigid particles in a confined flow of viscoelastic and strongly shear-thinning fluid at very small Reynolds numbers. Phys. Fluids 33 (5), 052001.CrossRefGoogle Scholar
Hintermuller, M.A., Reichel, E.K. & Jakoby, B. 2017 Modeling of acoustic streaming in viscoelastic fluids. In 2017 IEEE Sensors. IEEE.CrossRefGoogle Scholar
Hoque, S.Z., Nath, A. & Sen, A.K. 2021 Dynamical motion of a pair of microparticles at the acoustic pressure nodal plane under the combined effect of axial primary radiation and interparticle forces. J. Acoust. Soc. Am. 150 (1), 307–320.CrossRefGoogle ScholarPubMed
Joseph, D.D. 2013 Fluid Dynamics of Viscoelastic Liquids, vol. 84. Springer Science & Business Media.Google Scholar
Karlsen, J.T. & Bruus, H. 2015 Forces acting on a small particle in an acoustical field in a thermoviscous fluid. Phys. Rev. E 92 (4), 043010.CrossRefGoogle Scholar
Karthick, S., Pradeep, P.N., Kanchana, P. & Sen, A.K. 2018 Acoustic impedance-based size-independent isolation of circulating tumour cells from blood using acoustophoresis. Lab on a Chip 18 (24), 3802–3813.CrossRefGoogle ScholarPubMed
King, L.V. 1934 On the acoustic radiation pressure on spheres. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 147 (861), 212–240.Google Scholar
Laurell, T., Petersson, F. & Nilsson, A. 2007 Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 36 (3), 492–506.CrossRefGoogle ScholarPubMed
Lenshof, A. & Laurell, T. 2010 Continuous separation of cells and particles in microfluidic systems. Chem. Soc. Rev. 39 (3), 1203.CrossRefGoogle ScholarPubMed
Leshansky, A.M., Bransky, A., Korin, N. & Dinnar, U. 2007 Tunable nonlinear viscoelastic focusing in a microfluidic device. Phys. Rev. Lett. 98 (23), 1–4.CrossRefGoogle Scholar
Li, S., Ren, L., Huang, P.-H., Yao, X., Cuento, R.A., McCoy, J.P., Cameron, C.E., Levine, S.J. & Huang, T.J. 2016 Acoustofluidic transfer of inflammatory cells from human sputum samples. Anal. Chem. 88 (11), 5655–5661.CrossRefGoogle ScholarPubMed
Lighthill, S.J. 1978 Acoustic streaming. J. Sound Vib. 61 (3), 391–418.CrossRefGoogle Scholar
Malik, L., Nath, A., Nandy, S., Laurell, T. & Sen, A.K. 2022 Acoustic particle trapping driven by axial primary radiation force in shaped traps. Phys. Rev. E 105 (3), 1–15.CrossRefGoogle ScholarPubMed
Muller, P.B., Barnkob, R., Jensen, M.J.H. & Bruus, H. 2012 A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces. Lab on a Chip 12 (22), 4617.CrossRefGoogle ScholarPubMed
Muller, P.B. & Bruus, H. 2014 Numerical study of thermoviscous effects in ultrasound-induced acoustic streaming in microchannels. Phys. Rev. E 90 (4), 043016.CrossRefGoogle ScholarPubMed
Muller, P.B., Rossi, M., Marín, Á.G., Barnkob, R., Augustsson, P., Laurell, T., Kähler, C.J. & Bruus, H. 2013 Ultrasound-induced acoustophoretic motion of microparticles in three dimensions. Phys. Rev. E 88 (2), 023006.CrossRefGoogle ScholarPubMed
Nath, A., Malik, L. & Sen, A.K. 2021 Combined acoustic relocation and acoustophoretic migration for particle transfer between co-flowing fluids in a microchannel. Phys. Rev. Fluids 6 (4), 44201.CrossRefGoogle Scholar
Oldroyd, J.G. 1950 On the formulation of rheological equations of state. Proc. R. Soc. Lond. A Math. Phys. Sci. 200 (1063), 523–541.Google Scholar
Pan, W., Filobelo, L., Pham, N.D.Q., Galkin, O., Uzunova, V.V. & Vekilov, P.G. 2009 Viscoelasticity in homogeneous protein solutions. Phys. Rev. Lett. 102 (5), 058101.CrossRefGoogle ScholarPubMed
Petersson, F., Nilsson, A., Holm, C., Jönsson, H. & Laurell, T. 2004 Separation of lipids from blood utilizing ultrasonic standing waves in microfluidic channels. Analyst 129, 938–943.CrossRefGoogle ScholarPubMed
Rainer, F. & Ribitsch, V. 1985 Viscoelastic properties of normal human synovia and their relation to biomechanics. Z. Rheumatol. 44 (3), 114–119.Google ScholarPubMed
Rouse, P.E. 1953 A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 21 (7), 1272–1280.CrossRefGoogle Scholar
Sajeesh, P. & Sen, A.K. 2013 Particle separation and sorting in microfluidic devices: a review. Microfluid Nanofluid 17 (1), 1–52.CrossRefGoogle Scholar
Settnes, M. & Bruus, H. 2012 Forces acting on a small particle in an acoustical field in a viscous fluid. Phys. Rev. E 85 (1), 016327.CrossRefGoogle Scholar
Stokes, J.R. & Davies, G.A. 2007 Viscoelasticity of human whole saliva collected after acid and mechanical stimulation. Biorheology 44 (3), 141–160.Google ScholarPubMed
Thurston, G.B. 1972 Viscoelasticity of human blood. Biophys. J. 12 (9), 1205–1217.CrossRefGoogle ScholarPubMed
Tirtaatmadja, V., McKinley, H.G. & Cooper-White, J.J. 2006 Drop formation and breakup of low viscosity elastic fluids: effects of molecular weight and concentration. Phys. Fluids 18 (4), 043101.CrossRefGoogle Scholar
Vargas, C., Campos-Silva, I., Méndez, F., Arcos, J. & Bautista, O. 2022 Acoustic streaming in maxwell fluids generated by standing waves in two-dimensional microchannels. J. Fluid Mech. 933, A59.CrossRefGoogle Scholar
Yosioka, K. 1955 Acoustic radiation pressure on a compressible sphere. Acta Acust. United Acust. 5 (3), 167–173.Google Scholar
Yuan, D., Zhao, Q., Yan, S., Tang, S.-Y., Alici, G., Zhang, J. & Li, W. 2018 Recent progress of particle migration in viscoelastic fluids. Lab on a Chip 18 (4), 551–567.CrossRefGoogle ScholarPubMed
Zimm, B.H. 1956 Dynamics of polymer molecules in dilute solution: viscoelasticity, flow birefringence and dielectric loss. J. Chem. Phys. 24 (2), 269–278.CrossRefGoogle Scholar
Supplementary material: File

Sujith et al. supplementary material

Sujith et al. supplementary material
Download Sujith et al. supplementary material(File)
File 6.9 MB