Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-01T04:51:39.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid dynamics of frozen precipitation at the air–water interface

Published online by Cambridge University Press:  29 December 2021

Mehdi Vahab ,
David Murphy Open the ORCID record for David Murphy [Opens in a new window]  and
Kourosh Shoele Open the ORCID record for Kourosh Shoele [Opens in a new window]
Mehdi Vahab
Affiliation:
Department of Mechanical Engineering, Joint College of Engineering, Florida A&M University-Florida State University, Tallahassee, FL32310, USA
David Murphy
Affiliation:
Department of Mechanical Engineering, University of South Florida, Tampa, FL33620, USA
Kourosh Shoele*
Affiliation:
Department of Mechanical Engineering, Joint College of Engineering, Florida A&M University-Florida State University, Tallahassee, FL32310, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

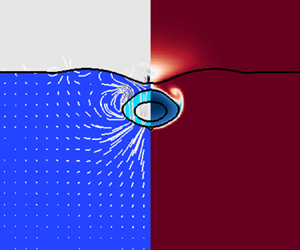
Precipitation in the forms of snow, hail, and rain plays a critical role in the exchange of mass, momentum and heat at the surfaces of lakes and seas. However, the microphysics of these interactions are not well understood. Motivated by recent observations, we study the physics of the impact of a single frozen canonical particle, such as snow and hail, onto the surface of a liquid bath using a numerical model. The descent, melting, bubble formation and thermal transport characteristics of this system are examined. Three distinct response regimes, namely particle impact, ice melting and vortex ring descent, have been identified and characterized. The melting rate and air content of the snow particle are found to be leading factors affecting the formation of a coherent vortex ring, the vertical descent of melted liquid and the vortex-induced transportation of the released gas bubble to lower depths. It is found that the water temperature can substantially alter the rate of phase change and subsequent flow and thermal transport, while the particle temperature has minimal effect on the process. Finally, the effects of the Reynolds, Weber and Stefan numbers are examined and it is shown that the Reynolds number modifies the strength of the vortex ring and induces the most significant effect on the flow dynamics of the snow particle. Also, the change of Weber number primarily alters the initial phases of snow–bath interaction while modifying the Stefan number of the snow particle essentially determines the system response in its later stages.

JFM classification

Geophysical and Geological Flows: Air/sea interactions Phase change: Solidification/melting
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 933 , 25 February 2022 , A36
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adhikari, A., Liu, C. & Kulie, M.S. 2018 Global distribution of snow precipitation features and their properties from 3 years of gpm observations. J. Clim. 31 (10), 3731–3754.CrossRefGoogle Scholar
Akhmetov, D.G. 2009 Vortex Rings. Springer Science & Business Media.CrossRefGoogle Scholar
Alavi, S., Passandideh-Fard, M. & Mostaghimi, J. 2012 Simulation of semi-molten particle impacts including heat transfer and phase change. J. Thermal Spray technol. 21 (6), 1278–1293.CrossRefGoogle Scholar
Ameen, F.R., Coney, J.E.R. & Sheppard, C.G.W. 1991 Experimental study of melting ice cylinders in a warm air cross-flow. Intl J. Refrig. 14 (3), 168–175.CrossRefGoogle Scholar
Baskin, K., Flores, K.M. & Weisensee, P.B. 2020 Heat transfer and melt dynamics of millimetric ice particles impacting a heated water bath. Intl J. Heat Mass Transfer 146, 118830.CrossRefGoogle Scholar
Belden, J., Hurd, R.C., Jandron, M.A., Bower, A.F. & Truscott, T.T. 2016 Elastic spheres can walk on water. Nat. Commun. 7 (1), 1–10.Google ScholarPubMed
Blanchard, D.C. & Woodcock, A.H. 1957 Bubble formation and modification in the sea and its meteorological significance. Tellus 9 (2), 145–158.CrossRefGoogle Scholar
Boroditsky, L. & Ramscar, M. 2001 First, we assume a spherical cow$\ldots$. Behav. Brain Sci. 24 (4), 656–657.CrossRefGoogle Scholar
Cao, Y., Faghri, A. & Chang, W.S. 1989 A numerical analysis of Stefan problems for generalized multi-dimensional phase-change structures using the enthalpy transforming model. Intl J. Heat Mass Transfer 32 (7), 1289–1298.CrossRefGoogle Scholar
Carlson, M., Mucha, P.J., Van Horn III, R.B. & Turk, G. 2002 Melting and flowing. In Proceedings of the 2002 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, pp. 167–174.Google Scholar
Chapman, D.S. & Critchlow, P.R. 1967 Formation of vortex rings from falling drops. J. Fluid Mech. 29 (1), 177–185.CrossRefGoogle Scholar
Chaudhary, G. & Li, R. 2014 Freezing of water droplets on solid surfaces: an experimental and numerical study. Exp. Thermal Fluid Sci. 57, 86–93.CrossRefGoogle Scholar
Dahle, A.K. & StJohn, D.H. 1998 Rheological behaviour of the mushy zone and its effect on the formation of casting defects during solidification. Acta Materialia 47 (1), 31–41.CrossRefGoogle Scholar
Davis, S.H. 2001 Theory of Solidification. Cambridge University Press.CrossRefGoogle Scholar
Dooley, B.S., Warncke, A.E., Gharib, M. & Tryggvason, G. 1997 Vortex ring generation due to the coalescence of a water drop at a free surface. Exp. Fluids 22 (5), 369–374.CrossRefGoogle Scholar
Duffy, G. & Bennartz, R. 2018 The role of melting snow in the ocean surface heat budget. Geophys. Res. Lett. 45 (18), 9782–9789.CrossRefGoogle Scholar
Dunnavan, E.L., Jiang, Z., Harrington, J.Y., Verlinde, J., Fitch, K. & Garrett, T.J. 2019 The shape and density evolution of snow aggregates. J. Atmos. Sci. 76 (12), 3919–3940.CrossRefGoogle Scholar
Eames, I. 2008 Disappearing bodies and ghost vortices. Phil. Trans. R. Soc. A: Math. Phys. Engng Sci. 366 (1873), 2219–2232.CrossRefGoogle ScholarPubMed
Engel, O.G. 1967 Initial pressure, initial flow velocity, and the time dependence of crater depth in fluid impacts. J. Appl. Phys. 38 (10), 3935–3940.CrossRefGoogle Scholar
Frank, F.C. 1952 Supercooling of liquids. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 215 (1120), 43–46.Google Scholar
Gaudet, S. 1998 Numerical simulation of circular disks entering the free surface of a fluid. Phys. Fluids 10 (10), 2489–2499.CrossRefGoogle Scholar
Gibou, F., Chen, L., Nguyen, D. & Banerjee, S. 2007 A level set based sharp interface method for the multiphase incompressible Navier–Stokes equations with phase change. J. Comput. Phys. 222 (2), 536–555.CrossRefGoogle Scholar
Gilbarg, D. & Anderson, R.A. 1948 Influence of atmospheric pressure on the phenomena accompanying the entry of spheres into water. J. Appl. Phys. 19 (2), 127–139.CrossRefGoogle Scholar
Glasheen, J.W. & McMahon, T.A. 1996 Vertical water entry of disks at low Froude numbers. Phys. Fluids 8 (8), 2078–2083.CrossRefGoogle Scholar
Grimado, P.B. & Boley, B.A. 1970 A numerical solution for the symmetric melting of spheres. Intl J. Numer. Meth. Engng 2 (2), 175–188.CrossRefGoogle Scholar
Gunn, R. & Kinzer, G.D. 1949 The terminal velocity of fall for water droplets in stagnant air. J. Meteorol. 6 (4), 243–248.2.0.CO;2>CrossRefGoogle Scholar
Gunn, K.L.S. & Marshall, J.S. 1958 The distribution with size of aggregate snowflakes. J. Atmos. Sci. 15 (5), 452–461.Google Scholar
Hao, Y.L. & Tao, Y.-X. 2002 Heat transfer characteristics of melting ice spheres under forced and mixed convection. J. Heat Transfer 124 (5), 891–903.CrossRefGoogle Scholar
Hills, R.N., Loper, D.E. & Roberts, P.H. 1983 A thermodynamically consistent model of a mushy zone. Q. J. Mech. Appl. Math. 36 (4), 505–540.CrossRefGoogle Scholar
Howison, S.D., Ockendon, J.R. & Wilson, S.K. 1991 Incompressible water-entry problems at small deadrise angles. J. Fluid Mech. 222, 215–230.CrossRefGoogle Scholar
Hurd, R.C., Belden, J., Jandron, M.A., Fanning, D.T., Bower, A.F. & Truscott, T.T. 2017 Water entry of deformable spheres. J. Fluid Mech. 824, 912–930.CrossRefGoogle Scholar
Ishii, M. & Hibiki, T. 2010 Thermo-Fluid Dynamics of Two-Phase Flow. Springer Science & Business Media.Google Scholar
Ishimoto, H. 2008 Radar backscattering computations for fractal-shaped snowflakes. J. Meteorol. Soc. Japan Ser. II 86 (3), 459–469.CrossRefGoogle Scholar
Jalaal, M., Kemper, D. & Lohse, D. 2019 Viscoplastic water entry. J. Fluid Mech. 864, 596–613.CrossRefGoogle Scholar
Jemison, M., Sussman, M. & Arienti, M. 2014 Compressible, multiphase semi-implicit method with moment of fluid interface representation. J. Comput. Phys. 279, 182–217.CrossRefGoogle Scholar
Jemison, M., Sussman, M. & Shashkov, M. 2015 Filament capturing with the multimaterial moment-of-fluid method. J. Comput. Phys. 285, 149–172.CrossRefGoogle Scholar
Jong-Leng, L. & Gray, N.B. 1996 Experimental study of splash generation in a flash smelting furnace. Metall. Mater. Trans. B 27 (4), 633–646.CrossRefGoogle Scholar
Juric, D. & Tryggvason, G. 1998 Computations of boiling flows. Intl J. Multiphase Flow 24 (3), 387–410.CrossRefGoogle Scholar
Korobkin, A.A. & Pukhnachov, V.V. 1988 Initial stage of water impact. Annu. Rev. Fluid Mech. 20 (1), 159–185.CrossRefGoogle Scholar
Kulie, M.S. & Milani, L. 2018 Seasonal variability of shallow cumuliform snowfall: a cloudsat perspective. Q. J. R. Meteorol. Soc. 144, 329–343.CrossRefGoogle Scholar
Lee, D.-G. & Kim, H.-Y. 2008 Impact of a superhydrophobic sphere onto water. Langmuir 24 (1), 142–145.CrossRefGoogle ScholarPubMed
Leng, L.J. 2001 Splash formation by spherical drops. J. Fluid Mech. 427, 73–105.CrossRefGoogle Scholar
Li, D., Zhang, J., Zhang, M., Huang, B., Ma, X. & Wang, G. 2019 Experimental study on water entry of spheres with different surface wettability. Ocean Engng 187, 106123.CrossRefGoogle Scholar
Liow, J.-L., Dickinson, W.H.R., Allan, M.J. & Gray, N.B. 1995 Study of slopping and splashing in a cylindrical bath with top-submerged injection. Metall. Mater. Trans. B 26 (4), 887–889.CrossRefGoogle Scholar
Liu, Y., Sussman, M., Lian, Y. & Hussaini, M.Y. 2020 A moment-of-fluid method for diffusion equations on irregular domains in multi-material systems. J. Comput. Phys. 402, 109017.CrossRefGoogle Scholar
Maruyama, K.-I. & Fujiyoshi, Y. 2005 Monte carlo simulation of the formation of snowflakes. J. Atmos. Sci. 62 (5), 1529–1544.CrossRefGoogle Scholar
Matrosov, S.Y., Reinking, R.F., Kropfli, R.A. & Bartram, B.W. 1996 Estimation of ice hydrometeor types and shapes from radar polarization measurements. J. Atmos. Ocean. Technol. 13 (1), 85–96.2.0.CO;2>CrossRefGoogle Scholar
May, A. 1951 Effect of surface condition of a sphere on its water-entry cavity. J. Appl. Phys. 22 (10), 1219–1222.CrossRefGoogle Scholar
McCue, S.W., Wu, B. & Hill, J.M. 2008 Classical two-phase stefan problem for spheres. Proc. R. Soc. A: Math. Phys. Engng Sci. 464 (2096), 2055–2076.CrossRefGoogle Scholar
Mcleod, P., Riley, D.S. & Sparks, R.S.J. 1996 Melting of a sphere in hot fluid. J. Fluid Mech. 327, 393–409.CrossRefGoogle Scholar
Morton, D., Rudman, M. & Jong-Leng, L. 2000 An investigation of the flow regimes resulting from splashing drops. Phys. Fluids 12 (4), 747–763.CrossRefGoogle Scholar
Murphy, D.W. 2016 Snowflake impact on the air-sea interface. In Bulletin of the American Physical Society, vol. 61, BAPS.2016.DFD.R13.4.Google Scholar
Murphy, D.W., Li, C., d'Albignac, V., Morra, D. & Katz, J. 2015 Splash behaviour and oily marine aerosol production by raindrops impacting oil slicks. J. Fluid Mech. 780, 536–577.CrossRefGoogle Scholar
Oguz, H.N. & Prosperetti, A. 1990 Bubble entrainment by the impact of drops on liquid surfaces. J. Fluid Mech. 219, 143–179.CrossRefGoogle Scholar
Oliver, J.M. 2007 Second-order wagner theory for two-dimensional water-entry problems at small deadrise angles. J. Fluid Mech. 572, 59–85.CrossRefGoogle Scholar
Palerme, C., Claud, C., Dufour, A., Genthon, C., Wood, N.B. & L'Ecuyer, T. 2017 Evaluation of antarctic snowfall in global meteorological reanalyses. Atmos. Res. 190, 104–112.CrossRefGoogle Scholar
Pasandideh-Fard, M., Chandra, S. & Mostaghimi, J. 2002 A three-dimensional model of droplet impact and solidification. Intl J. Heat Mass Transfer 45 (11), 2229–2242.CrossRefGoogle Scholar
Pasandideh-Fard, M., Qiao, Y.M., Chandra, S. & Mostaghimi, J. 1996 Capillary effects during droplet impact on a solid surface. Phys. Fluids 8 (3), 650–659.CrossRefGoogle Scholar
Passarelli, R.E. Jr & Srivastava, R.C. 1979 A new aspect of snowflake aggregation theory. J. Atmos. Sci. 36 (3), 484–493.2.0.CO;2>CrossRefGoogle Scholar
Peck, B. & Sigurdson, L. 1994 The three-dimensional vortex structure of an impacting water drop. Phys. Fluids 6 (2), 564–576.CrossRefGoogle Scholar
Pei, C., Vahab, M., Sussman, M. & Hussaini, M.Y. 2019 A hierarchical space-time spectral element and moment-of-fluid method for improved capturing of vortical structures in incompressible multi-phase/multi-material flows. J. Sci. Comput. 81 (3), 1527–1566.CrossRefGoogle Scholar
Prosperetti, A. & Oguz, H.N. 1993 The impact of drops on liquid surfaces and the underwater noise of rain. Annu. Rev. Fluid Mech. 25 (1), 577–602.CrossRefGoogle Scholar
Pruppacher, H.R. & Klett, J.D. 1980 Microphysics of clouds and precipitation. Nature 284 (5751), 88.CrossRefGoogle Scholar
Pruppacher, H.R. & Klett, J.D. 2012 Microphysics of Clouds and Precipitation, Reprinted 1980. Springer Science & Business Media.Google Scholar
Pumphrey, H.C. & Elmore, P.A. 1990 The entrainment of bubbles by drop impacts. J. Fluid Mech. 220, 539–567.CrossRefGoogle Scholar
Quested, T.E. & Greer, A.L. 2005 Athermal heterogeneous nucleation of solidification. Acta Materialia 53 (9), 2683–2692.CrossRefGoogle Scholar
Raessi, M., Thiele, M. & Amirzadeh, B. 2013 Computational simulation of the impact and freezing of micron-size water droplets on super-hydrophobic surfaces. In ASME 2013 Heat Transfer Summer Conference collocated with the ASME 2013 7th International Conference on Energy Sustainability and the ASME 2013 11th International Conference on Fuel Cell Science, Engineering and Technology, pp. V002T07A032. American Society of Mechanical Engineers.Google Scholar
Ray, B., Biswas, G. & Sharma, A. 2015 Regimes during liquid drop impact on a liquid pool. J. Fluid Mech. 768, 492–523.CrossRefGoogle Scholar
Rein, M. 1996 The transitional regime between coalescing and splashing drops. J. Fluid Mech. 306, 145–165.CrossRefGoogle Scholar
Reinhard, M. 2013 Free elastic plate impact into water. PhD thesis, University of East Anglia.Google Scholar
Rodriguez, F. & Mesler, R. 1988 The penetration of drop-formed vortex rings into pools of liquid. J. Colloid Interface Sci. 121 (1), 121–129.CrossRefGoogle Scholar
Saramito, P. 2016 Complex Fluids. Springer.CrossRefGoogle Scholar
Schmitt, C.G. & Heymsfield, A.J. 2010 The dimensional characteristics of ice crystal aggregates from fractal geometry. J. Atmos. Sci. 67 (5), 1605–1616.CrossRefGoogle Scholar
Shankar, P.N. & Kumar, M. 1995 Vortex rings generated by drops just coalescing with a pool. Phys. Fluids 7 (4), 737–746.CrossRefGoogle Scholar
Shin, S. & Juric, D. 2002 Modeling three-dimensional multiphase flow using a level contour reconstruction method for front tracking without connectivity. J. Comput. Phys. 180 (2), 427–470.CrossRefGoogle Scholar
Soloviev, A. & Lukas, R. 2013 The Near-Surface Layer of the Ocean: Structure, Dynamics and Applications, vol. 48. Springer Science & Business Media.Google Scholar
Tabakova, S., Feuillebois, F. & Radev, S. 2010 Freezing of a supercooled spherical droplet with mixed boundary conditions. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 466, pp. 1117–1134. The Royal Society.CrossRefGoogle Scholar
Tavakoli, F., Davis, S.H. & Kavehpour, H.P. 2015 Freezing of supercooled water drops on cold solid substrates: initiation and mechanism. J. Coatings Technol. Res. 12 (5), 869–875.CrossRefGoogle Scholar
Taylor, G.I. 1953 Formation of a vortex ring by giving an impulse to a circular disk and then dissolving it away. J. Appl. Phys. 24 (1), 104.CrossRefGoogle Scholar
Thiévenaz, V., Séon, T. & Josserand, C. 2019 Solidification dynamics of an impacted drop. J. Fluid Mech. 874, 756–773.CrossRefGoogle Scholar
Truscott, T.T. & Techet, A.H. 2009 a A spin on cavity formation during water entry of hydrophobic and hydrophilic spheres. Phys. Fluids 21 (12), 121703.CrossRefGoogle Scholar
Truscott, T.T. & Techet, A.H. 2009 b Water entry of spinning spheres. J. Fluid Mech. 625 (1), 135–165.CrossRefGoogle Scholar
Vahab, M., Pei, C., Hussaini, M.Y., Sussman, M. & Lian, Y. 2016 An adaptive coupled level set and moment-of-fluid method for simulating droplet impact and solidification on solid surfaces with application to aircraft icing. In 54th AIAA Aerospace Sciences Meeting, AIAA Paper 2016-1340.Google Scholar
Vahab, M., Shoele, K. & Sussman, M. 2018 Interaction of an oscillating flexible plate and nucleate pool boiling vapor bubble: fluid-structure interaction in a multimaterial multiphase system. In 2018 Fluid Dynamics Conference, AIAA Paper 2018-3718.Google Scholar
Vahab, M., Sussman, M. & Shoele, K. 2021 Fluid-structure interaction of thin flexible bodies in multi-material multi-phase systems. J. Comput. Phys. 429, 110008.CrossRefGoogle Scholar
Voller, V. & Cross, M. 1981 Accurate solutions of moving boundary problems using the enthalpy method. Intl J. Heat Mass Transfer 24 (3), 545–556.CrossRefGoogle Scholar
Westbrook, C.D., Ball, R.C., Field, P.R. & Heymsfield, A.J. 2004 Theory of growth by differential sedimentation, with application to snowflake formation. Phys. Rev. E 70 (2), 021403.CrossRefGoogle ScholarPubMed
Weymouth, G.D. & Triantafyllou, M.S. 2012 Global vorticity shedding for a shrinking cylinder. J. Fluid Mech. 702, 470–487.CrossRefGoogle Scholar
Worthington, A.M. 1908 A Study of Splashes. Longmans, Green, and Company.Google Scholar
Worthington, A.M. & Cole, R.S. 1897 V. Impact with a liquid surface, studied by the aid of instantaneous photography. Phil. Trans. R. Soc. Lond. Ser. A Containing Papers Math. Phys. Character 189, 137–148.Google Scholar
Worthington, A.M. & Cole, R.S. 1900 IV. Impact with a liquid surface studied by the aid of instantaneous photography. Paper II. Phil. Trans. R. Soc. Lond. Ser. A, Containing Papers Math. Phys. Character 194 (252–261), 175–199.Google Scholar
Wu, Y., Hannah, C.G., Thupaki, P., Mo, R. & Law, B. 2017 Effects of rainfall on oil droplet size and the dispersion of spilled oil with application to douglas channel, British Columbia, Canada. Mar. Pollution Bull. 114 (1), 176–182.CrossRefGoogle ScholarPubMed
Zappa, C.J., Ho, D.T., McGillis, W.R., Banner, M.L., Dacey, J.W.H., Bliven, L.F., Ma, B. & Nystuen, J. 2009 Rain-induced turbulence and air-sea gas transfer. J. Geophys. Res.: Oceans 114, C07009.Google Scholar