Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T11:53:51.190Z Has data issue: false hasContentIssue false
  • English
  • Français

Flows of liquid 4He due to oscillating grids

Published online by Cambridge University Press:  26 October 2017

P. Švančara  and
M. La Mantia Open the ORCID record for M. La Mantia [Opens in a new window]
P. Švančara
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague, Czech Republic
M. La Mantia*
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague, Czech Republic
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

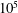We investigate cryogenic flows of liquid 4He between two grids oscillating in phase, at temperatures ranging from approximately 1.3 to 2.5 K, resulting in suitably defined Reynolds numbers up to $10^{5}$. We specifically study the flow-induced motions of small particles suspended in the fluid by using the particle tracking velocimetry technique. We focus on turbulent flows of superfluid 4He that occur below approximately 2.2 K and are known to display, in certain conditions, features different from those observed in flows of classical viscous fluids, such as water. We find that, at large enough length scales, larger than the mean distance between quantized vortices, representing the quantum length scale of the flow, the shapes of the velocity and velocity increment statistical distributions are very similar to those obtained in turbulent flows of viscous fluids. The experimental outcome strongly supports the view that, in the range of investigated parameters, particles probing flows of superfluid 4He behave as if they were tracking classical flows.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Quantum fluids Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 578 - 599
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babuin, S., Ľvov, V. S., Pomyalov, A., Skrbek, L. & Varga, E. 2016 Coexistence and interplay of quantum and classical turbulence in superfluid 4He: decay, velocity decoupling, and counterflow energy spectra. Phys. Rev. B 94, 174504.Google Scholar
Babuin, S., Varga, E., Skrbek, L., Lévêque, E. & Roche, P.-E. 2014 Effective viscosity in quantum turbulence: a steady-state approach. Europhys. Lett. 106, 24006.Google Scholar
Baggaley, A. W. & Barenghi, C. F. 2011 Quantum turbulent velocity statistics and quasiclassical limit. Phys. Rev. E 84, 067301.Google Scholar
Barenghi, C. F., Skrbek, L. & Sreenivasan, K. R. 2014 Introduction to quantum turbulence. Proc. Natl Acad. Sci. USA 111, 4647–4652.Google Scholar
Bewley, G. P., Lathrop, D. P. & Sreenivasan, K. R. 2006 Superfluid helium: visualization of quantized vortices. Nature 441, 588.Google Scholar
Blum, D. B., Kunwar, S. B., Johnson, J. & Voth, G. A. 2010 Effects of nonuniversal large scales on conditional structure functions in turbulence. Phys. Fluids 22, 015107.Google Scholar
Chevillard, L., Castaing, B., Arnoedo, A., Lévêque, E. & Pinton, J.-F. 2012 A phenomenological theory of Eulerian and Lagrangian velocity fluctuations in turbulent flows. C. R. Phys. 13, 899–928.CrossRefGoogle Scholar
De Silva, I. P. D. & Fernando, H. J. S. 1994 Oscillating grids as a source of nearly isotropic turbulence. Phys. Fluids 6, 2455–2464.Google Scholar
Donnelly, R. J. & Barenghi, C. F. 1998 The observed properties of liquid helium at the saturated vapor pressure. J. Phys. Chem. Ref. Data 27, 1217–1274.Google Scholar
Duda, D., Švančara, P., La Mantia, M., Rotter, M. & Skrbek, L. 2015 Visualization of viscous and quantum flows of liquid 4He due to an oscillating cylinder of rectangular cross section. Phys. Rev. B 92, 064519.Google Scholar
Gao, J., Guo, W., Ľvov, V. S., Pomyalov, A., Skrbek, L., Varga, E. & Vinen, W. F. 2016 Decay of counterflow turbulence in superfluid 4He. JETP Lett. 103, 648–652.Google Scholar
Guo, W., La Mantia, M., Lathrop, D. P. & Van Sciver, S. W. 2014 Visualization of two-fluid flows of superfluid helium-4. Proc. Natl Acad. Sci. USA 111, 4653–4658.Google Scholar
Honey, R. E., Hershberger, R., Donnelly, R. J. & Bolster, D. 2014 Oscillating-grid experiments in water and superfluid helium. Phys. Rev. E 89, 053016.Google ScholarPubMed
Isaza, J. C., Salazar, R. & Warhaft, Z. 2014 On grid-generated turbulence in the near- and far field regions. J. Fluid Mech. 753, 402–426.Google Scholar
Krstulovic, G. 2016 Grid superfluid turbulence and intermittency at very low temperature. Phys. Rev. E 93, 063104.Google ScholarPubMed
La Mantia, M. 2016 Particle trajectories in thermal counterflow of superfluid helium in a wide channel of square cross section. Phys. Fluids 28, 024102.Google Scholar
La Mantia, M. 2017 Particle dynamics in wall-bounded thermal counterflow of superfluid helium. Phys. Fluids 29, 065102.Google Scholar
La Mantia, M., Chagovets, T. V., Rotter, M. & Skrbek, L. 2012 Testing the performance of a cryogenic visualization system on thermal counterflow by using hydrogen and deuterium solid tracers. Rev. Sci. Instrum. 83, 055109.Google Scholar
La Mantia, M., Duda, D., Rotter, M. & Skrbek, L. 2013 Lagrangian accelerations of particles in superfluid turbulence. J. Fluid Mech. 717, R9.Google Scholar
La Mantia, M. & Skrbek, L. 2014a Quantum, or classical turbulence? Europhys. Lett. 105, 46002.CrossRefGoogle Scholar
La Mantia, M. & Skrbek, L. 2014b Quantum turbulence visualized by particle dynamics. Phys. Rev. B 90, 014519.Google Scholar
La Mantia, M., Švančara, P., Duda, D. & Skrbek, L. 2016 Small-scale universality of particle dynamics in quantum turbulence. Phys. Rev. B 94, 184512.Google Scholar
Marakov, A., Gao, J., Guo, W., Van Sciver, S. W., Ihas, G. G., McKinsey, D. N. & Vinen, W. F. 2015 Visualization of the normal-fluid turbulence in counterflowing superfluid 4He. Phys. Rev. B 91, 094503.CrossRefGoogle Scholar
Maurer, J. & Tabeling, P. 1998 Local investigation of superfluid turbulence. Europhys. Lett. 43, 29–34.CrossRefGoogle Scholar
Mordant, M., Lévêque, E. & Pinton, J.-F. 2004a Experimental and numerical study of the Lagrangian dynamics of high Reynolds turbulence. New J. Phys. 6, 116.Google Scholar
Mordant, N., Crawford, A. M. & Bodenschatz, E. 2004b Three-dimensional structure of the Lagrangian acceleration in turbulent flows. Phys. Rev. Lett. 93, 214501.Google Scholar
Mordant, N., Metz, P., Michel, O. & Pinton, J.-F. 2001 Measurement of Lagrangian velocity in fully developed turbulence. Phys. Rev. Lett. 87, 214501.CrossRefGoogle ScholarPubMed
Noullez, A., Wallace, G., Lempert, W., Miles, R. B. & Frisch, U. 1997 Transverse velocity increments in turbulent flow using the RELIEF technique. J. Fluid Mech. 339, 287–307.Google Scholar
Paoletti, M. S., Fisher, M. E., Sreenivasan, K. R. & Lathrop, D. P. 2008 Velocity statistics distinguish quantum turbulence from classical turbulence. Phys. Rev. Lett. 101, 154501.Google Scholar
Qureshi, N. M., Arrieta, U., Baudet, C., Cartellier, A., Gagne, Y. & Bourgoin, M. 2008 Acceleration statistics of inertial particles in turbulent flow. Eur. Phys. J. B 66, 531–536.CrossRefGoogle Scholar
Qureshi, N. M., Bourgoin, M., Baudet, C., Cartellier, A. & Gagne, Y. 2007 Turbulent transport of material particles: an experimental study of finite size effects. Phys. Rev. Lett. 99, 184502.Google Scholar
Salort, J., Baudet, C., Castaing, B., Chabaud, B., Daviaud, F., Didelot, T., Diribarne, P., Dubrulle, B., Gagne, Y., Gauthier, F. et al. 2010 Turbulent velocity spectra in superfluid flows. Phys. Fluids 22, 125102.Google Scholar
Salort, J., Chabaud, B., Lévêque, E. & Roche, P.-E. 2012 Energy cascade and the four-fifths law in superfluid turbulence. Europhys. Lett. 97, 34006.Google Scholar
Sbalzarini, I. F. & Koumoutsakos, P. 2005 Feature point tracking and trajectory analysis for video imaging in cell biology. J. Struct. Biol. 151, 182–195.Google Scholar
Skrbek, L., Gordeev, A. V. & Soukup, F. 2003 Decay of counterflow He II turbulence in a finite channel: possibility of missing links between classical and quantum turbulence. Phys. Rev. E 67, 047302.Google Scholar
Skrbek, L. & Sreenivasan, K. R. 2012 Developed quantum turbulence and its decay. Phys. Fluids 24, 011301.Google Scholar
Smith, M. R., Donnelly, R. J., Goldenfeld, N. & Vinen, W. F. 1993 Decay of vorticity in homogeneous turbulence. Phys. Rev. Lett. 71, 2583–2586.Google Scholar
Stalp, S. R., Skrbek, L. & Donnelly, R. J. 1999 Decay of grid turbulence in a finite channel. Phys. Rev. Lett. 82, 4831–4834.Google Scholar
Švančara, P. & La Mantia, M. 2017 Particle dynamics in 4He flows due to oscillating grids. In Proc. Conference Topical Problems of Fluid Mechanics (ed. Šimurda, D. & Bodnár, T.), pp. 295–302. Institute of Thermomechanics of the Academy of Sciences of the Czech Republic.Google Scholar
Sy, N. F., Bourgoin, M., Diribarne, P., Gibert, M. & Rousset, B. 2015 Oscillating grid high Reynolds experiments in superfluid. In Proc. 15th European Turbulence Conference (ed. Boersma, B. J., Breugem, W.-P., Elsinga, G. E., Pecnik, R., Poelma, C. & Westerweel, J.), Paper no. 318. Delft University of Technology.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence. Springer.Google Scholar
Van Sciver, S. W. 2012 Helium Cryogenics. Springer.Google Scholar
Varga, E., Babuin, S. & Skrbek, L. 2015 Second-sound studies of coflow and counterflow of superfluid 4He in channels. Phys. Fluids 27, 065101.CrossRefGoogle Scholar
Villermaux, E., Sixou, B. & Gagne, Y. 1995 Intense vortical structures in grid-generated turbulence. Phys. Fluids 7, 2008–2013.Google Scholar
Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.Google Scholar
Vinen, W. F. & Skrbek, L. 2014 Quantum turbulence generated by oscillating structures. Proc. Natl. Acad. Sci. USA 111, 4699–4706.Google Scholar
Zmeev, D. E., Walmsley, P. M., Golov, A. I., McClintock, P. V. E., Fisher, S. N. & Vinen, W. F. 2015 Dissipation of quasiclassical turbulence in superfluid 4He. Phys. Rev. Lett. 115, 155303.Google Scholar