Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T07:07:21.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow-induced vibration of D-section cylinders: an afterbody is not essential for vortex-induced vibration

Published online by Cambridge University Press:  20 July 2018

J. Zhao Open the ORCID record for J. Zhao [Opens in a new window] ,
K. Hourigan  and
M. C. Thompson
J. Zhao*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
K. Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
M. C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

While it has been known that an afterbody (i.e. the structural part of a bluff body downstream of the flow separation points) plays an important role affecting the wake characteristics and even may change the nature of the flow-induced vibration (FIV) of a structure, the question of whether an afterbody is essential for the occurrence of one particular common form of FIV, namely vortex-induced vibration (VIV), still remains. This has motivated the present study to experimentally investigate the FIV of an elastically mounted forward- or backward-facing D-section (closed semicircular) cylinder over the reduced velocity range 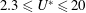$2.3\leqslant U^{\ast }\leqslant 20$, where 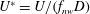$U^{\ast }=U/(f_{nw}D)$. Here, 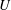$U$ is the free-stream velocity, 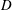$D$ the cylinder diameter and $f_{nw}$ the natural frequency of the system in quiescent fluid (water). The normal orientation with the body’s flat surface facing upstream is known to be subject to another common form of FIV, galloping, while the reverse D-section with the body’s curved surface facing upstream, due to the lack of an afterbody, has previously been reported to be immune to VIV. The fluid–structure system was modelled on a low-friction air-bearing system in conjunction with a recirculating water channel facility to achieve a low mass ratio (defined as the ratio of the total oscillating mass to that of the displaced fluid mass). Interestingly, through a careful overall examination of the dynamic responses, including the vibration amplitude and frequency, fluid forces and phases, our new findings showed that the D-section exhibits a VIV-dominated response for 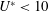$U^{\ast }<10$, galloping-dominated response for 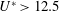$U^{\ast }>12.5$, and a transition regime with a VIV–galloping interaction in between. Also observed for the first time were interesting wake modes associated with these response regimes. However, in contrast to previous studies at high Reynolds number (defined by 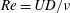$Re=UD/\unicode[STIX]{x1D708}$, with $\unicode[STIX]{x1D708}$ the kinematic viscosity), which have showed that the D-section was subject to ‘hard’ galloping that required a substantial initial amplitude to trigger, it was observed in the present study that the D-section can gallop softly from rest. Surprisingly, on the other hand, it was found that the reverse D-section exhibits pure VIV features. Remarkable similarities were observed in a direct comparison with a circular cylinder of the same mass ratio, in terms of the onset $U^{\ast }$ of significant vibration, the peak amplitude (only approximately 6 % less than that of the circular cylinder), and also the fluid forces and phases. Of most significance, this study shows that an afterbody is not essential for VIV at low mass and damping ratios.

JFM classification

Aerodynamics: Aerodynamics Flow Control: Flow Control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 317 - 343
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.Google Scholar
Bearman, P. W. & Davies, M. E. 1977 The flow about oscillating bluff structures. In Proceedings of the International Conference on Wind Effects on Buildings and Structures (ed. Eaton, K. J.), pp. 285–295. Cambridge University Press.Google Scholar
Bearman, P. W., Gartshore, I. S., Maull, D. & Parkinson, G. V. 1987 Experiments on flow-induced vibration of a square-section cylinder. J. Fluids Struct. 1 (1), 19–34.Google Scholar
Blevins, R. D. 1990 Flow-Induced Vibration. Von Nostrand Reinhold.Google Scholar
Brooks, P. N. H.1960 Experimental investigation of the aeroelastic instability of bluff two-dimensional cylinders. Masters Thesis, University of British Columbia.Google Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2001 Force and wake modes of an oscillating cylinder. J. Fluids Struct. 15, 523–532.Google Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2005 Controlled oscillations of a cylinder: forces and wake modes. J. Fluid Mech. 538, 31–69.Google Scholar
Cheers, F.1950 A note on galloping conductors. National Research Council of Canada, Report MT-14.Google Scholar
Corless, R. M. & Parkinson, G. V. 1988 A model of the combined effects of vortex-induced oscillation and galloping. J. Fluids Struct. 2, 203–220.Google Scholar
Den Hartog, J. P. 1932 Transmission line vibration due to sleet. Trans. Am. Inst. Electrical Engrs 51 (4), 1074–1076.Google Scholar
Den Hartog, J. P. 1956 Mechanical Vibrations. McGraw-Hill.Google Scholar
Feng, C. C.1968 The measurement of vortex induced effects in flow past stationary and oscillating circular and D-section cylinders. M.A.Sc. Thesis, University of British Columbia.Google Scholar
Fouras, A., Lo Jacono, D. & Hourigan, K. 2008 Target-free stereo PIV: a novel technique with inherent error estimation and improved accuracy. Exp. Fluids 44 (2), 317–329.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2002 Resonance forever: existence of a critical mass and an infinite regime of resonance in vortex-induced vibration. J. Fluid Mech. 473, 147–166.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2006 Defining the ‘modified Griffin plot’ in vortex-induced vibration: revealing the effect of Reynolds number using controlled damping. J. Fluid Mech. 561, 147–180.Google Scholar
Griffin, O. M. & Koopman, G. H. 1982 Some recent studies of vortex shedding with application to marine tubulars and risers. Trans. ASME J. Energy Resour. Technol. 104, 2–13.Google Scholar
Griffin, O. M., Skop, R. A. & Koopmann, G. H. 1973 The vortex-excited resonant vibrations of circular cylinders. J. Sound Vib. 31 (2), 235–249.Google Scholar
Harris, G. O. 1948 Galloping Conductors II. University of Notre-Dame.Google Scholar
Khalak, A. & Williamson, C. H. K. 1996 Dynamics of a hydroelastic structure with very low mass and damping. J. Fluids Struct. 10 (5), 455–472.Google Scholar
Khalak, A. & Williamson, C. H. K. 1997 Fluid forces and dynamics of a hydroelastic structure with very low mass and damping. J. Fluids Struct. 11 (8), 973–982.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7–8), 813–851.Google Scholar
Lanchester, F. W. 1907 Aerodynamics. Constable.Google Scholar
Luo, S. C., Chew, Y. T. & Ng, Y. T. 2003 Hysteresis phenomenon in the galloping oscillation of a square cylinder. J. Fluids Struct. 18 (1), 103–118.Google Scholar
Meneghini, J., Saltara, F., Fregonesi, R. & Yamamoto, C. 2005 Vortex-induced vibration on flexible cylinders. In Numerical Models in Fluid–Structure Interaction (ed. Chakrabarti, S. K.), WIT Press.Google Scholar
Morse, T. L. & Williamson, C. H. K. 2009 Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 634, 5–39.Google Scholar
Naudascher, E. & Rockwell, D. 2005 Flow-Induced Vibrations: An Engineering Guide. Dover.Google Scholar
Nemes, A., Zhao, J., Lo Jacono, D. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.Google Scholar
Novak, M. & Tanaka, H. 1974 Effect of turbulence on galloping instability. J. Engng Mech. Div. 100 (1), 27–47.Google Scholar
Païdoussis, M., Price, S. & De Langre, E. 2010 Fluid–Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Parkinson, G. 1989 Phenomena and modelling of flow-induced vibrations of bluff bodies. Prog. Aerosp. Sci. 26, 169–224.Google Scholar
Parkinson, G. V. 1963 Aeroelastic galloping in one degree of freedom. In Symposium Wind Effects on Buildings and Structures, pp. 582–609. National Physical Laboratory.Google Scholar
Parkinson, G. V. & Smith, J. D. 1964 The square prism as an aeroelastic non-linear oscillator. Q. J. Mech. Appl. Maths 17 (2), 225–239.Google Scholar
Sareen, A., Zhao, J., Logacono, D., Sheridon, J., Hourigan, K. & Thompson, M. C. 2018 Vortex-induced vibration of a rotating sphere. J. Fluid Mech. 837, 258–292.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.Google Scholar
Soti, A. K., Zhao, J., Thompson, M. C., Sheridan, J. & Bhardwaj, R. 2018 Damping effects on vortex-induced vibrations of a circular cylinder and power extraction. J. Fluids Struct. 81, 289–308.Google Scholar
Twigge-Molecey, C. F. M. & Baines, M. D. 1974 Unsteady pressure distribution due to vortex-induced vibration of a triangular cylinder. In Flow Induced Structural Vibrations, pp. 433–442. Springer.Google Scholar
Weaver, D. S. & Veljkovic, I. 2005 Vortex shedding and galloping of open semi-circular and parabolic cylinders in cross-flow. J. Fluids Struct. 21 (1), 65–74.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibration. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Wong, K. W. L., Zhao, J., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2017 Experimental investigation of flow-induced vibration of a rotating circular cylinder. J. Fluid Mech. 829, 486–511.Google Scholar
Wong, K. W. L., Zhao, J., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2018 Experimental investigation of flow-induced vibration of a sinusoidally rotating circular cylinder. J. Fluid Mech. 848, 430–466.Google Scholar
Zhao, J., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2014a Chaotic vortex induced vibrations. Phys. Fluids 26 (12), 121702.Google Scholar
Zhao, J., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2014b Fluid–structure interaction of a square cylinder at different angles of attack. J. Fluid Mech. 747, 688–721.Google Scholar
Zhao, J., Lo Jacono, D., Sheridan, J., Hourigan, K. & Thompson, M. C. 2018 Experimental investigation of in-line flow-induced vibration of a rotating cylinder. J. Fluid Mech. 847, 664–699.Google Scholar

Zhao et al. supplementary movie 1

Phase-averaged vorticity contours showing 2S mode at U*=3.4 for the case of α=0°.

Download Zhao et al. supplementary movie 1(Video)
Video 2.2 MB

Zhao et al. supplementary movie 2

Phase-averaged vorticity contours showing 2S mode at U*=4.0 for the case of α=0°.

Download Zhao et al. supplementary movie 2(Video)
Video 2.2 MB

Zhao et al. supplementary movie 3

Phase-averaged vorticity contours showing 2Po mode at U*=5.0 for the case of α=0°.

Download Zhao et al. supplementary movie 3(Video)
Video 2.3 MB

Zhao et al. supplementary movie 4

Phase-averaged vorticity contours showing 2To mode at U*=6.0 for the case of α=0°.

Download Zhao et al. supplementary movie 4(Video)
Video 2.4 MB

Zhao et al. supplementary movie 5

Phase-averaged vorticity contours showing 2To mode at U*=6.3 for the case of α=0°.

Download Zhao et al. supplementary movie 5(Video)
Video 2.4 MB

Zhao et al. supplementary movie 6

Phase-averaged vorticity contours showing 2To mode at U*=8.0 for the case of α=0°.

Download Zhao et al. supplementary movie 6(Video)
Video 2.4 MB

Zhao et al. supplementary movie 7

Phase-averaged vorticity contours showing 2T mode at U*=12.0 for the case of α=0°.

Download Zhao et al. supplementary movie 7(Video)
Video 3 MB

Zhao et al. supplementary movie 8

Phase-averaged vorticity contours showing 2T-C mode at U*=6.0 for the case of α=0°.

Download Zhao et al. supplementary movie 8(Video)
Video 3.1 MB

Zhao et al. supplementary movie 9

Phase-averaged vorticity contours showing 2S mode at U*=4.0 for the case of α=180°.

Download Zhao et al. supplementary movie 9(Video)
Video 2.2 MB

Zhao et al. supplementary movie 10

Phase-averaged vorticity contours showing 2S mode at U*=6.0 for the case of α=180°.

Download Zhao et al. supplementary movie 10(Video)
Video 1.9 MB

Zhao et al. supplementary movie 11

Phase-averaged vorticity contours showing 2S mode at U*=8.0 for the case of α=180°.

Download Zhao et al. supplementary movie 11(Video)
Video 1.6 MB