Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Du, Lin
and
Sun, Xiaofeng
2019.
Noise reduction by feedback rotary oscillation of a three-dimensional circular cylinder.
Journal of Fluids and Structures,
Vol. 84,
Issue. ,
p.
421.
Monreal Jiménez, Cintia
Oviedo Tolentino, Francisco
Gutiérrez Urueta, Geydy
and
Romero-Méndez, Ricardo
2020.
Experimental research on vortex-induced vibrations of flexible circular cylinders at low Reynolds number: revealing atypical branches.
Ocean Engineering,
Vol. 195,
Issue. ,
p.
106754.
McQueen, T.
Zhao, J.
Sheridan, J.
and
Thompson, M. C.
2020.
Feedback control of flow-induced vibration of a sphere.
Journal of Fluid Mechanics,
Vol. 889,
Issue. ,
Hasheminejad, Seyyed M.
and
Fallahi, Ramin
2021.
Effects of force and moment actuation in active two dimensional VIV control of an elastic circular cylinder in power-law fluid flow.
Ocean Engineering,
Vol. 238,
Issue. ,
p.
109752.
Wang, Sijie
Hu, Jun
Huang, Can
and
Yu, Yong
2021.
Graphics processing unit-accelerated smoothed particle hydrodynamics—Finite difference method and the application for the flow around a cylinder with forced motions.
Physics of Fluids,
Vol. 33,
Issue. 12,
Esmaeili, Mostafa
and
Rabiee, Amir Hossein
2021.
Active feedback VIV control of sprung circular cylinder using TDE-iPID control strategy at moderate Reynolds numbers.
International Journal of Mechanical Sciences,
Vol. 202-203,
Issue. ,
p.
106515.
Mosaferi, Amir Aslan
Esmaeili, Mostafa
and
Rabiee, Amir Hossein
2022.
Effect of aligned magnetic field on the 2DOF VIV suppression and convective heat transfer characteristics of a circular cylinder.
International Communications in Heat and Mass Transfer,
Vol. 130,
Issue. ,
p.
105807.
Zheng, Hanxu
and
Wang, Jiasong
2022.
Flow-induced vibration of flexible cylinders covered by fixed fairings with different chord-thickness ratios.
Marine Structures,
Vol. 86,
Issue. ,
p.
103299.
Barrero-Gil, A.
Serruys, S.
and
Velazquez, A.
2022.
Influence of cross-section shape on energy harvesting from transverse flow-induced vibrations of bluff bodies.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Hasheminejad, Seyyed M.
and
Fallahi, Ramin
2022.
Effects of cylinder cross-sectional geometry and blockage ratio on VIV-based mixing performance in two dimensional laminar channel flow.
Chemical Engineering and Processing - Process Intensification,
Vol. 177,
Issue. ,
p.
108987.
Lopez-Gavilan, P.
and
Barrero-Gil, A.
2023.
On the limits of Particle Image Velocimetry with continuous wave lasers.
Experimental Thermal and Fluid Science,
Vol. 144,
Issue. ,
p.
110873.
Lo, Jonathan C.C.
Hourigan, Kerry
Zhao, Jisheng
and
Thompson, Mark C.
2024.
Data-driven active control of a thin elliptical cylinder undergoing transverse flow-induced vibrations.
Journal of Fluid Mechanics,
Vol. 1001,
Issue. ,
Ren, Feng
Wen, Xin
and
Tang, Hui
2024.
Model-Free Closed-Loop Control of Flow Past a Bluff Body: Methods, Applications, and Emerging Trends.
Actuators,
Vol. 13,
Issue. 12,
p.
488.
Ren, Feng
Wang, Chenglei
Song, Jian
and
Tang, Hui
2024.
Deep reinforcement learning finds a new strategy for vortex-induced vibration control.
Journal of Fluid Mechanics,
Vol. 990,
Issue. ,
Barrero-Gil, A.
2024.
Flow mixing enhancement by crossflow induced oscillations of an open semicircular cylinder.
Experimental Thermal and Fluid Science,
Vol. 159,
Issue. ,
p.
111283.
Li, Xintao
Luo, Yuping
Liang, Xiao
Ge, Mingwei
and
Zhang, Weiwei
2024.
Rotationary feedback control of the cylinder wake flow using a linear dynamic model.
Physics of Fluids,
Vol. 36,
Issue. 12,
Tian, Wenlong
Zhang, Chen
Mao, Zhaoyong
Li, Bo
Zhang, Tianqi
and
Song, Baowei
2024.
Numerical investigation on the suppression of vortex-induced vibration system by assembling different rotors based on quasi-active control method.
Ocean Engineering,
Vol. 311,
Issue. ,
p.
119015.
Esmaeili, Mostafa
Fakhri Vayqan, Hossein
and
Rabiee, Amir Hossein
2025.
The role of flow angle in mixed convection and vortex-induced vibration of a thermally controlled elastic cylinder.
International Journal of Numerical Methods for Heat & Fluid Flow,
Vol. 35,
Issue. 2,
p.
799.
Esmaeili, Mostafa
Fakhri Vayqan, Hossein
and
Rabiee, Amir Hossein
2025.
Impact of Temperature-Induced Buoyancy on the 2DOF-VIV of a Heated/Cooled Cylinder.
Arabian Journal for Science and Engineering,
Vol. 50,
Issue. 4,
p.
2807.
He, Haoyu
Ding, Lin
Song, Tian
Sun, Yue
and
Ran, Jingyu
2025.
Comparative analysis on heat transfer and flow-induced vibration of rotating cylinders with different degrees of freedom.
International Communications in Heat and Mass Transfer,
Vol. 164,
Issue. ,
p.
108915.
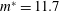 $m^{\ast }=11.7$,
$m^{\ast }=11.7$, 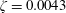 $\unicode[STIX]{x1D701}=0.0043$) so the analysis is focused on the role of the rotation law and the reduced velocity. The Reynolds number based on the diameter of the cylinder ranges from 1500 to 10 000. Results are presented in terms of steady-state oscillation characterization (say, amplitude and frequency) and wake-pattern topology, which was obtained through digital particle image velocimetry. Both laws are able to either reduce or enhance oscillations, but they do it in a different way. A rotation law proportional to the cylinder’s displacement is more effective to enhance oscillations. For high enough actuation, a galloping-type response has been found, with a persistent growth of the amplitude of oscillations with the reduced velocity that shows a new desynchronized mode of vortex shedding. On the other hand, a rotation law proportional to the cylinder’s transverse velocity is more efficient to reduce oscillations. In this case only vortex-induced-type responses have been found. A quasi-steady theoretical model has been developed, which helps to explain why a galloping-type response may appear when rotation is proportional to cylinder displacement and is able to predict reasonably the amplitude of oscillations in those cases. The model also explains why a galloping-type response is not expected to occur when rotation is proportional to the cylinder’s velocity.
$\unicode[STIX]{x1D701}=0.0043$) so the analysis is focused on the role of the rotation law and the reduced velocity. The Reynolds number based on the diameter of the cylinder ranges from 1500 to 10 000. Results are presented in terms of steady-state oscillation characterization (say, amplitude and frequency) and wake-pattern topology, which was obtained through digital particle image velocimetry. Both laws are able to either reduce or enhance oscillations, but they do it in a different way. A rotation law proportional to the cylinder’s displacement is more effective to enhance oscillations. For high enough actuation, a galloping-type response has been found, with a persistent growth of the amplitude of oscillations with the reduced velocity that shows a new desynchronized mode of vortex shedding. On the other hand, a rotation law proportional to the cylinder’s transverse velocity is more efficient to reduce oscillations. In this case only vortex-induced-type responses have been found. A quasi-steady theoretical model has been developed, which helps to explain why a galloping-type response may appear when rotation is proportional to cylinder displacement and is able to predict reasonably the amplitude of oscillations in those cases. The model also explains why a galloping-type response is not expected to occur when rotation is proportional to the cylinder’s velocity.