Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T10:02:54.430Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow reversals in Rayleigh–Bénard convection with non-Oberbeck–Boussinesq effects

Published online by Cambridge University Press:  08 June 2016

Shu-Ning Xia ,
Zhen-Hua Wan ,
Shuang Liu ,
Qi Wang  and
De-Jun Sun
Shu-Ning Xia
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
Zhen-Hua Wan*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
Shuang Liu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
Qi Wang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
De-Jun Sun*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
*
†Email addresses for correspondence: [email protected]; [email protected]
†Email addresses for correspondence: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

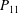Flow reversals in two-dimensional Rayleigh–Bénard convection led by non-Oberbeck–Boussinesq (NOB) effects due to large temperature differences are studied by direct numerical simulation. Perfect gas is chosen as the working fluid and the Prandtl number is 0.71 for the reference state. If NOB effects are included, the flow pattern $P_{11}$ with only one dominant roll often becomes unstable by the growth of the cold corner roll, which sometimes results in cession-led flow reversals. By exploiting the vorticity transport equation, it is found that the asymmetries of buoyancy and viscous forces are responsible for the growth of the cold corner roll because both such asymmetries cause an imbalance between the corner rolls and the large-scale circulation (LSC). The buoyancy force near the cold wall increases and decreases near the hot wall originating from the temperature-dependent isobaric thermal expansion coefficient 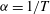${\it\alpha}=1/T$ if NOB effects are included. Moreover, the decreased dissipation due to lower viscosity is favourable for the growth of the cold corner roll, while the increased viscosity further suppresses the growth of the hot corner roll. Finally, it is found that the boundary layer near the cold wall plays an important role in the mass transport from LSC to corner rolls subject to mass conservation.

JFM classification

Convection: Convection Convection: Convection in cavities
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 628 - 642
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2007 Non-Oberbeck–Boussinesq effects in gaseous Rayleigh–Bénard convection. Phys. Rev. Lett. 98 (5), 054501.Google Scholar
Ahlers, G., Brown, E., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.Google Scholar
Ahlers, G., Calzavarini, E., Araujo, F. F., Funfschilling, D., Grossmann, S., Lohse, D. & Sugiyama, K. 2008 Non-Oberbeck–Boussinesq effects in turbulent thermal convection in ethane close to the critical point. Phys. Rev. E 77 (4), 046302.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503.CrossRefGoogle Scholar
Bathe, K.-J., Brezzi, F. & Pironneau, O. 2001 Computational Fluid and Solid Mechanics, vol. 2. Springer.Google Scholar
Benzi, R. 2005 Flow reversal in a simple dynamical model of turbulence. Phys. Rev. Lett. 95 (2), 024502.CrossRefGoogle Scholar
Breuer, M. & Hansen, U. 2009 Turbulent convection in the zero Reynolds number limit. Eur. Phys. Lett. 86 (2), 24004.Google Scholar
Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007a Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98 (13), 134501.Google Scholar
Brown, E. & Ahlers, G. 2007b Temperature gradients, and search for non-Boussinesq effects, in the interior of turbulent Rayleigh–Bénard convection. Eur. Phys. Lett. 80 (1), 14001.CrossRefGoogle Scholar
Chandra, M. & Verma, M. K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83 (6), 067303.Google Scholar
Chandra, M. & Verma, M. K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110 (11), 114503.Google Scholar
Fontenele Araujo, F., Grossmann, S. & Lohse, D. 2005 Wind reversals in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95 (8), 084502.Google Scholar
Gissinger, C. 2012 A new deterministic model for chaotic reversals. Eur. J. Mech. B 85 (4), 1–12.Google Scholar
Glatzmaier, G. A., Coe, R. S., Hongre, L. & Roberts, P. H. 1999 The role of the Earth’s mantle in controlling the frequency of geomagnetic reversals. Nature 401 (6756), 885–890.Google Scholar
Glatzmaier, G. A. & Roberts, P. H. 1995 A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 377, 203–209.Google Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26 (5), 055111.CrossRefGoogle Scholar
Horn, S., Shishkina, O. & Wagner, C. 2013 On non-Oberbeck–Boussinesq effects in three-dimensional Rayleigh–Bénard convection in glycerol. J. Fluid Mech. 724, 175–202.Google Scholar
Huang, S.-D., Wang, F., Xi, H.-D., Xia, K.-Q.& others 2015 Comparative experimental study of fixed temperature and fixed heat flux boundary conditions in turbulent thermal convection. Phys. Rev. Lett. 115 (15), 154502.CrossRefGoogle ScholarPubMed
Huang, S.-D. & Xia, K.-Q. 2016 Effects of geometric confinement in quasi-2-D turbulent Rayleigh–Bénard convection. J. Fluid Mech. 794, 639–654.Google Scholar
Huang, Y.-X. & Zhou, Q. 2013 Counter-gradient heat transport in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 737, R3.CrossRefGoogle Scholar
Le Quéré, P., Weisman, C., Paillère, H., Vierendeels, J., Dick, E., Becker, R., Braack, M. & Locke, J. 2005 Modelling of natural convection flows with large temperature differences: a benchmark problem for low Mach number solvers. Part 1: reference solutions. Math. Modelling Numer. Anal. 39 (03), 609–616.Google Scholar
Liu, B., Zhang, J. & others, 2008 Self-induced cyclic reorganization of free bodies through thermal convection. Phys. Rev. Lett. 100 (24), 244501.Google Scholar
Moin, P. & Verzicco, R. 2016 On the suitability of second-order accurate discretizations for turbulent flow simulations. Eur. J. Mech. B 55, 242–245.Google Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2015 Reversals of the large-scale circulation in quasi-2D Rayleigh–Bénard convection. J. Fluid Mech. 778, R5.CrossRefGoogle Scholar
Paolucci, S.1982 Filtering of sound from the Navier–Stokes equations. NASA STI/Recon Tech. Rep. N, 83, 26036.Google Scholar
Podvin, B. & Sergent, A. 2015 A large-scale investigation of wind reversal in a square Rayleigh–Bénard cell. J. Fluid Mech. 766, 172–201.CrossRefGoogle Scholar
Resagk, C., du Puits, R., Thess, A., Dolzhansky, F. V., Grossmann, S., Araujo, F. F. & Lohse, D. 2006 Oscillations of the large scale wind in turbulent thermal convection. Phys. Fluids 18 (9), 095105.CrossRefGoogle Scholar
Sameen, A., Verzicco, R. & Sreenivasan, K. R. 2008 Non-Boussinesq convection at moderate Rayleigh numbers in low temperature gaseous helium. Phys. Scr. 2008 (T132), 014053.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.Google Scholar
Sreenivasan, K. R., Bershadskii, A. & Niemela, J. J. 2002 Mean wind and its reversal in thermal convection. Phys. Rev. E 65 (5), 056306.Google Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2007 Non-Oberbeck–Boussinesq effects in two-dimensional Rayleigh–Bénard convection in glycerol. Eur. Phys. Lett. 80 (3), 34002.CrossRefGoogle Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2009 Flow organization in two-dimensional non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. J. Fluid Mech. 637, 105–135.CrossRefGoogle Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105 (3), 034503.Google Scholar
de Vahl Davis, G. & Jones, I. P. 1983 Natural convection in a square cavity: a comparison exercise. Intl J. Numer. Meth. Fluids 3 (3), 227–248.Google Scholar
Verma, M. K., Ambhire, S. C. & Pandey, A. 2015 Flow reversals in turbulent convection with free-slip walls. Phys. Fluids 27 (4), 047102.Google Scholar
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 3 (5), 052001.CrossRefGoogle Scholar
Yanagisawa, T., Hamano, Y. & Sakuraba, A. 2015 Flow reversals in low-Prandtl-number Rayleigh–Bénard convection controlled by horizontal circulations. Phys. Rev. E 92 (2), 023018.Google ScholarPubMed

Xia et al. supplementary movie

Flow reversal of approximate one period with density as background. Ra=7×105, ϵ=0.4. The black solid line is one of vorticity contour with zero value.

Download Xia et al. supplementary movie(Video)
Video 6.3 MB

Xia et al. supplementary movie

Flow reversal of half a period with temperature as background. Ra=107, ϵ=0.4.

Download Xia et al. supplementary movie(Video)
Video 7 MB

Xia et al. supplementary movie

Flow reversal of half a period with temperature as background. Ra=7×106. OB approximation is adopted with modulation of gravity acceleration in which χ1=0.3 and χ2= 0.7 and modulation of dynamical viscosity μ imitating that of ϵ=0.4.

Download Xia et al. supplementary movie(Video)
Video 9 MB