Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T03:10:19.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow of a falling liquid curtain into a pool

Published online by Cambridge University Press:  17 February 2014

Harumichi Kyotoh ,
Kazuki Fujita ,
Koichi Nakano  and
Takeaki Tsuda
Harumichi Kyotoh*
Affiliation:
Department of Engineering Mechanics and Systems, University of Tsukuba, Tsukuba, Ibaraki 302-8573, Japan
Kazuki Fujita
Affiliation:
Research and Development Department, Yuken Kogyo Co., Ltd, Ayase, Kanagawa 252-1113, Japan
Koichi Nakano
Affiliation:
Technology Development Center, Dai Nippon Printing Co., Ltd., Tsukuba, Ibaraki 300-2646, Japan
Takeaki Tsuda
Affiliation:
Technology Development Center, Dai Nippon Printing Co., Ltd., Tsukuba, Ibaraki 300-2646, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the low-Weber-number flow of a liquid curtain bridged between two vertical edge guides and a pool surface. Three flow patterns, namely, steady vertical flow, steady oblique flow, and oscillatory oblique flow, are observed in our experiment. These patterns are caused by the Coanda effect of the jet around the meniscus that is formed in the matching region common to the liquid curtain and the pool surface. Here, the deflection angle of the jet is greater than 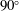$90^\circ $. The equation describing the motion of the liquid curtain applicable for a finite curtain slope is obtained using the intrinsic coordinate system in which the distance along the curtain is selected as one of the coordinates, and the equation of the meniscus motion is derived by considering the conservation of momentum. The curtain deformations of oblique flows are analysed by generating numerical simulations of these equations, and the simulation results are then compared with experimental results. Also, the period of oscillatory oblique flow is discussed and explained via the response analyses of the curtain, and the result shows that the period of the oscillations is close to that of the most amplified mode of the liquid curtain. Further, the detachment angle of the jet is discussed in relation to the Coanda effect of the jet in the meniscus.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Wakes/Jets: Jets Interfacial Flows (free surface): Liquid bridges
Type
Papers
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , pp. 350 - 376
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arne, W., Marheineke, N., Meister, A. & Wegener, R. 2010 Numerical analysis of Cosserat rod and string models for viscous jets in rotational spinning processes. Math. Models Meth. Appl. Sci. 20 (10), 1941–1965.Google Scholar
Erwin, F. & Idelchik, I. E. 1989 Flow Resistance: a Design Guide for Engineers. Hemisphere.Google Scholar
Fekete, G. I. 1963 Coanda flow of a two-dimensional wall jet on the outside of a circular cylinder. Tech. Rep. Mechanical Engineering Research Laboratories 63–11. McGill University.Google Scholar
Finnicum, D. S., Weinstein, S. J. & Ruschak, K. J. 1993 The effect of applied pressure on the shape of a two-dimensional liquid curtain falling under the influence of gravity. J. Fluid Mech. 255, 647–665.Google Scholar
van de Fliert, B. W., Howell, P. D. & Ockendon, J. R. 1995 Pressure-driven flow of a thin viscous sheet. J. Fluid Mech. 292, 359–376.CrossRefGoogle Scholar
Fric, T. F. & Gharib, M. 1990 Wake formation of the transverse jet. Bull. Am. Phys. Soc. 35, 2338–2347.Google Scholar
Fric, T. F. & Roshko, A. 1994 Vortical structure in the wake of a transverse jet. J. Fluid Mech. 279, 1–47.Google Scholar
Haniu, H. & Ramaprian, B. R. 1989 Studies on two-dimensional curved nonbuoyant jets in cross flow. Trans. ASME: J. Fluids Engng 111 (1), 78–86.Google Scholar
Higgins, B. G. & Scriven, L. E. 1979 Interfacial shape and evolution equations for liquid films and other viscocapillary flows. Ind. Engng Chem. Fundam. 18 (3), 208–215.Google Scholar
Ida, M. P. 1995 The dynamics of thin liquid films. PhD thesis, Northwestern University, Evanston.Google Scholar
Ida, M. P. & Miksis, M. J. 1998 The dynamics of thin films I: general theory. SIAM J. Appl. Maths 58 (2), 456–473.Google Scholar
Kheshgi, H. S., Kistler, S. F. & Scriven, L. E. 1992 Rising and falling film flows: Viewed from a first-order approximation. Chem. Engng Sci. 47–3, 683–694.CrossRefGoogle Scholar
Kistler, S. F. 1984 The fluid mechanics of curtain coating and other related viscous free surface flows with contact lines. PhD thesis, University of Minnesota.Google Scholar
Kistler, S. F. & Schweizer, P. M. 1997 Liquid Film Coating: Scientific Principles and their Technological Implications. Kluwer.CrossRefGoogle Scholar
Kyotoh, H., Tsuda, T., Takagi, M. & Nakano, K. 2009 Momentum integral equation for an unsteady falling liquid curtain. Kyoto University Research Information Repository 1645, 194–201 (in Japanese).Google Scholar
Newman, B. G. 1961 The deflexion of plane jets by adjacent boundaries-coanda effect. In Boundary Layer and Flow Control (ed. Lachmann, G. V.), pp. 232–264. Pergamon.Google Scholar
Neuendorf, R. & Wygnanski, I. 1999 On a turbulent wall jet flowing over a circular cylinder. J. Fluid Mech. 381, 1–25.Google Scholar
Pope, S. G. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Ribe, N. M., Habibi, M. & Bonn, D. 2006 Stability of liquid rope coiling. Phys. Fluids 18, 084102.Google Scholar
Sebilleau, J., Limat, L. & Eggers, J. 2009 Flow separation from a stationary meniscus. J. Fluid Mech. 633, 137–145.Google Scholar
Takagi, M. 2010 Transfer of a falling liquid curtain to liquid or solid surfaces. Master’s thesis, Graduate School of Systems and Information Engineering, University of Tsukuba (in Japanese).Google Scholar
Weinstein, S. J., Clarke, A., Moon, A. G. & Simister, E. A. 1997 Time-dependent equations governing the shape of a two-dimensional liquid curtain, Part 1: Theory. Phys. Fluids 9, 3625–3636.CrossRefGoogle Scholar
Weinstein, S. J., Hoff, J. W. & Ross, D. S. 1998 Time-dependent equations governing the shape of a three-dimensional liquid curtain. Phys. Fluids 10, 1815–1818.CrossRefGoogle Scholar
Yao, J. & Stewart, D. S. 1996 Dynamics of multi-dimensional detonation. J. Fluid Mech. 309, 225–275.Google Scholar

Kyotoh et al. supplementary movie

Steady oblique flow in figure 4(a)

Download Kyotoh et al. supplementary movie(Video)
Video 4.8 MB

Kyotoh et al. supplementary movie

Steady oblique flow in figure 4(a)

Download Kyotoh et al. supplementary movie(Video)
Video 1.8 MB

Kyotoh et al. supplementary movie

Steady oblique flow in figure 4(b)

Download Kyotoh et al. supplementary movie(Video)
Video 5.3 MB

Kyotoh et al. supplementary movie

Steady oblique flow in figure 4(b)

Download Kyotoh et al. supplementary movie(Video)
Video 1.8 MB

Kyotoh et al. supplementary movie

Oscillatory oblique flow in figure 5(a)

Download Kyotoh et al. supplementary movie(Video)
Video 15.9 MB

Kyotoh et al. supplementary movie

Oscillatory oblique flow in figure 5(a)

Download Kyotoh et al. supplementary movie(Video)
Video 5.6 MB

Kyotoh et al. supplementary movie

Oscillatory oblique flow in figure 5(b)

Download Kyotoh et al. supplementary movie(Video)
Video 15.7 MB

Kyotoh et al. supplementary movie

Oscillatory oblique flow in figure 5(b)

Download Kyotoh et al. supplementary movie(Video)
Video 6.4 MB

Kyotoh et al. supplementary movie

Overview of the curtain behavior

Download Kyotoh et al. supplementary movie(Video)
Video 6.2 MB

Kyotoh et al. supplementary movie

Overview of the curtain behavior

Download Kyotoh et al. supplementary movie(Video)
Video 3.1 MB