Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T14:42:28.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow instabilities and impact of ramp–isolator junction on shock–boundary-layer interactions in a supersonic intake

Published online by Cambridge University Press:  09 December 2022

Nikhil Khobragade Open the ORCID record for Nikhil Khobragade [Opens in a new window] ,
S. Unnikrishnan  and
Rajan Kumar
Nikhil Khobragade*
Affiliation:
Department of Mechanical Engineering, FAMU-FSU College of Engineering, Florida Center for Advanced Aero-Propulsion, FL 32310 USA
S. Unnikrishnan
Affiliation:
Department of Mechanical Engineering, FAMU-FSU College of Engineering, Florida Center for Advanced Aero-Propulsion, FL 32310 USA
Rajan Kumar
Affiliation:
Department of Mechanical Engineering, FAMU-FSU College of Engineering, Florida Center for Advanced Aero-Propulsion, FL 32310 USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

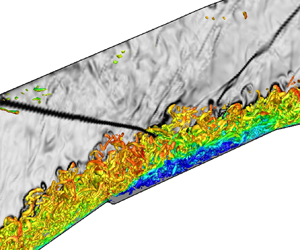
Boundary layer instabilities and shock–boundary-layer interactions (SBLIs) critically affect the performance and safe operation of mixed-compression air intakes. We present a computational study anchored in companion experiments, to evaluate the multimodal mechanisms driving the dynamics of the external compression ramp flow and the cowl SBLI in a Mach $3$ intake. Boundary layer transition over the external ramp is first analysed through a global linear analysis, and the linear estimates are further validated through direct numerical simulations. The separation bubble over the ramp harbours three-dimensional stationary instabilities that induce transition, under the influence of secondary instabilities driven by the shear layer modes of the bubble. The interaction of the resulting turbulized boundary layer with the cowl shock at the ramp–isolator junction and its control through geometrical modification constitutes the second part of the study. We tested a faceted (baseline) and a notched (modified) junction design to evaluate its impact on the low-, mid- and high-frequency scales generated at the cowl SBLI region. In relation to the baseline case, the notched geometry effectively locks the separation point of the bubble, thus attenuating the upstream low-frequency breathing motion. The notch also energizes the midfrequency content through vortex shedding in a well-developed shear layer, which persists into the isolator, thus assisting in an efficient compression process through cross-stream mixing of near-wall flow. The isolator boundary layer in the notched design exhibits relatively lower static pressures and higher velocity fluctuations, which are conducive to improving the flow stability, unstart margin and efficiency of high-speed propulsion systems.

JFM classification

Aerodynamics: High-speed flow Compressible Flows: Compressible boundary layers Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 953 , 25 December 2022 , A30
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adams, N.A. 2000 Direct simulation of the turbulent boundary layer along a compression ramp at $M= 3$ and $Re\theta = 1685$. J. Fluid Mech. 420, 47–83.CrossRefGoogle Scholar
Adler, M.C., Gonzalez, D.R., Stack, C.M. & Gaitonde, D.V. 2018 Synthetic generation of equilibrium boundary layer turbulence from modeled statistics. Comput. Fluids 165, 127–143.CrossRefGoogle Scholar
Agostini, L., Larchevêque, L., Dupont, P., Debiève, J.-F. & Dussauge, J.-P. 2012 Zones of influence and shock motion in a shock/boundary-layer interaction. AIAA J. 50 (6), 1377–1387.CrossRefGoogle Scholar
Alam, M. & Sandham, N.D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 410, 1–28.CrossRefGoogle Scholar
Ali, M.Y., Alvi, F., Manisankar, C., Verma, S. & Venkatakrishnan, L. 2011 Studies on the control of shock wave-boundary layer interaction using steady microactuators. In 41st AIAA Fluid Dynamics Conference and Exhibit, AIAA Paper 2011-3425.Google Scholar
Anderson, D., Tannehill, J. & Pletcher, R. 1984 Computational Fluid Mechanics and Heat Transfer. McGraw-Hill.Google Scholar
Aubard, G., Gloerfelt, X. & Robinet, J.-C. 2013 Large-eddy simulation of broadband unsteadiness in a shock/boundary-layer interaction. AIAA J. 51 (10), 2395–2409.CrossRefGoogle Scholar
Bagheri, S., Åkervik, E., Brandt, L. & Henningson, D.S. 2009 Matrix-free methods for the stability and control of boundary layers. AIAA J. 47 (5), 1057–1068.CrossRefGoogle Scholar
Balsara, D.S. & Shu, C.-W. 2000 Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. J. Comput. Phys. 160 (2), 405–452.Google Scholar
Beam, R. & Warming, R. 1978 An implicit factored scheme for the compressible Navier–Stokes equations. AIAA J. 16 (4), 393–402.CrossRefGoogle Scholar
Bhagatwala, A. & Lele, S.K. 2009 A modified artificial viscosity approach for compressible turbulence simulations. J. Comput. Phys. 228 (14), 4965–4969.CrossRefGoogle Scholar
Caraballo, E., Webb, N., Little, J., Kim, J.-H. & Samimy, M. 2009 Supersonic inlet flow control using plasma actuators. In 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA Paper 2009-924.Google Scholar
Cherubini, S., Robinet, J.-C., De Palma, P. & Alizard, F. 2010 The onset of three-dimensional centrifugal global modes and their nonlinear development in a recirculating flow over a flat surface. Phys. Fluids 22 (11), 114102.CrossRefGoogle Scholar
De Vanna, F., Picano, F., Benini, E. & Quinn, M.K. 2021 Large-eddy simulations of the unsteady behaviour of a hypersonic intake at $m$ach 5. AIAA J. 59 (10), 1–14.Google Scholar
Délery, J., Marvin, J.G. & Reshotko, E. 1986 Shock-wave boundary layer interactions. Tech. Rep. Advisory Group for Aerospace Research and Development Neuilly-Sur-Seine (France).Google Scholar
Dolling, D.S. 2001 Fifty years of shock-wave/boundary-layer interaction research: what next? AIAA J. 39 (8), 1517–1531.CrossRefGoogle Scholar
Dolling, D.S. & Murphy, M.T. 1983 Unsteadiness of the separation shock wave structure in a supersonic compression ramp flowfield. AIAA J. 21 (12), 1628–1634.CrossRefGoogle Scholar
Duan, J., Li, X., Li, X. & Liu, H. 2021 Direct numerical simulation of a supersonic turbulent boundary layer over a compression–decompression corner. Phys. Fluids 33 (6), 065111.CrossRefGoogle Scholar
Dupont, P., Piponniau, S., Sidorenko, A. & Debiève, J.F. 2008 Investigation by particle image velocimetry measurements of oblique shock reflection with separation. AIAA J. 46 (6), 1365–1370.Google Scholar
Eaton, J.K. & Johnston, J.P. 1981 A review of research on subsonic turbulent flow reattachment. AIAA J. 19 (9), 1093–1100.CrossRefGoogle Scholar
Floryan, J.M. 1991 On the Görtler instability of boundary layers. Prog. Aerosp. Sci. 28 (3), 235–271.CrossRefGoogle Scholar
Gaitonde, D.V. 2015 Progress in shock wave/boundary layer interactions. Prog. Aerosp. Sci. 72, 80–99.CrossRefGoogle Scholar
Garmann, D.J. 2013 Characterization of the vortex formation and evolution about a revolving wing using high-fidelity simulation. PhD thesis, University of Cincinnati.Google Scholar
Gerolymos, G.A. 1990 Implicit multiple-grid solution of the compressible Navier–Stokes equations using $k-\epsilon$ turbulence closure. AIAA J. 28 (10), 1707–1717.Google Scholar
Hartfield, R.J Jr., Hollo, S.D. & McDaniel, J.C. 1993 Planar measurement technique for compressible flows using laser-induced iodine fluorescence. AIAA J. 31 (3), 483–490.CrossRefGoogle Scholar
Hildebrand, N., Dwivedi, A., Nichols, J.W., Jovanović, M.R. & Candler, G.V. 2018 Simulation and stability analysis of oblique shock-wave/boundary-layer interactions at mach 5.92. Phys. Rev. Fluids 3 (1), 013906.CrossRefGoogle Scholar
Holden, H.A. & Babinsky, H. 2005 Separated shock-boundary-layer interaction control using streamwise slots. J. Aircraft 42 (1), 166–171.CrossRefGoogle Scholar
Hosseinverdi, S. & Fasel, H.F. 2019 Numerical investigation of laminar–turbulent transition in laminar separation bubbles: the effect of free-stream turbulence. J. Fluid Mech. 858, 714–759.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P.A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.CrossRefGoogle Scholar
Hunt, R.L. & Gamba, M. 2019 On the origin and propagation of perturbations that cause shock train inherent unsteadiness. J. Fluid Mech. 861, 815–859.CrossRefGoogle Scholar
Karthick, S.K. 2021 Shock and shear layer interactions in a confined supersonic cavity flow. Phys. Fluids 33 (6), 066102.CrossRefGoogle Scholar
Kaushik, M. 2019 Experimental studies on micro-vortex generator controlled shock/boundary-layer interactions in mach 2.2 intake. Intl J. Aeronaut. Space Sci. 20 (3), 584–595.CrossRefGoogle Scholar
Khobragade, N., Gustavsson, J., Kumar, R., Kirby, S., Birch, T.J., Mai, C.L. & Taylor, R.H. 2020 Characterization of bleedless shockwave boundary layer interaction control for high speed intakes. In AIAA Scitech 2020 Forum, AIAA Paper 2020-2091.Google Scholar
Khobragade, N., Unnikrishnan, S. & Kumar, R. 2021 Linear and nonlinear flow analysis of elements of a supersonic inlet. AIAA J. 59 (11), 4392–4409.CrossRefGoogle Scholar
Krishnan, L., Sandham, N.D. & Steelant, J. 2009 Shock-wave/boundary-layer interactions in a model scramjet intake. AIAA J. 47 (7), 1680–1691.CrossRefGoogle Scholar
Kumar, R., Ali, M.Y., Alvi, F.S. & Venkatakrishnan, L. 2011 Generation and control of oblique shocks using microjets. AIAA J. 49 (12), 2751–2759.CrossRefGoogle Scholar
Kurelek, J.W., Lambert, A.R. & Yarusevych, S. 2016 Coherent structures in the transition process of a laminar separation bubble. AIAA J. 54 (8), 2295–2309.Google Scholar
van Leer, B. 1979 Towards the ultimate conservation difference scheme V, a second-order sequel to Godunov's method. J. Comput. Phys. 32, 101–136.CrossRefGoogle Scholar
Li, W. & Liu, H. 2019 Large-eddy simulation of shock-wave/boundary-layer interaction control using a backward facing step. Aerosp. Sci. Technol. 84, 1011–1019.CrossRefGoogle Scholar
Li, F. & Malik, M.R. 1995 Fundamental and subharmonic secondary instabilities of Görtler vortices. J. Fluid Mech. 297, 77–100.CrossRefGoogle Scholar
Lin, J.C.M. & Pauley, L.L. 1996 Low-Reynolds-number separation on an airfoil. AIAA J. 34 (8), 1570–1577.CrossRefGoogle Scholar
Lüdeke, H. & Sandham, N. 2010 Direct numerical simulation of the transition process in a separated supersonic ramp flow. In 40th Fluid Dynamics Conference and Exhibit, AIAA Paper 2010-4470.Google Scholar
Morgan, B., Duraisamy, K. & Lele, S.K. 2014 Large-eddy simulations of a normal shock train in a constant-area isolator. AIAA J. 52 (3), 539–558.CrossRefGoogle Scholar
Narasimha, R. & Sreenivasan, K.R. 1973 Relaminarization in highly accelerated turbulent boundary layers. J. Fluid Mech. 61 (3), 417–447.CrossRefGoogle Scholar
Oswatitsch, K. 1980 Pressure recovery for missiles with reaction propulsion at high supersonic speeds (the efficiency of shock diffusers). In Contributions to the Development of Gasdynamics, pp. 290–323. Springer.Google Scholar
Pauley, L.L., Moin, P. & Reynolds, W.C. 1990 The structure of two-dimensional separation. J. Fluid Mech. 220, 397–411.CrossRefGoogle Scholar
Piponniau, S., Dussauge, J.-P., Debieve, J.-F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.CrossRefGoogle Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at $M= 2.25$. Phys. Fluids 18 (6), 065113.CrossRefGoogle Scholar
Priebe, S. & Martín, M.P. 2012 Low-frequency unsteadiness in shock wave–turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.Google Scholar
Pulliam, T.H. & Chaussee, D.S. 1981 A diagonal form of an implicit approximate-factorization algorithm. J. Comput. Phys. 39 (2), 347–363.Google Scholar
Ranjan, R., Unnikrishnan, S. & Gaitonde, D. 2020 A robust approach for stability analysis of complex flows using high-order Navier–Stokes solvers. J. Comput. Phys. 403, 109076.CrossRefGoogle Scholar
Ranjan, R., Unnikrishnan, S., Robinet, J.-C. & Gaitonde, D. 2021 Global transition dynamics of flow in a lid-driven cubical cavity. Theor. Comput. Fluid Dyn. 35 (3), 397–418.CrossRefGoogle Scholar
Rizzetta, D.P. & Visbal, M.R. 1993 Comparative numerical study of two turbulence models for airfoil static and dynamic stall. AIAA J. 31 (4), 784–786.CrossRefGoogle Scholar
Rodriguez, D. & Theofilis, V. 2010 Structural changes of laminar separation bubbles induced by global linear instability. J. Fluid Mech. 655, 280–305.CrossRefGoogle Scholar
Rodríguez, D., Gennaro, E.M. & Souza, L.F. 2018 Self-excited primary and secondary instability of laminar separation bubbles. J. Fluid Mech. 906, A13.Google Scholar
Roe, P.L. 1981 Approximate Riemann solvers, parameter vectors and difference schemes. J. Comput. Phys. 43, 357–372.CrossRefGoogle Scholar
Schmid, P.J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Seddon, J. & Goldsmith, E.L. 1999 Intake Aerodynamics, vol. 2. Blackwell Science Boston.CrossRefGoogle Scholar
Sfeir, A. 1966 Supersonic flow separation on a backward facing step. Tech. Rep. California Univ Berkeley Div of Aeronautical Sciences.Google Scholar
Shi, F., Gao, Z., Jiang, C. & Lee, C.-H. 2021 Numerical investigation of shock-turbulent mixing layer interaction and shock-associated noise. Phys. Fluids 33 (2), 025105.CrossRefGoogle Scholar
Shu, C.W. & Osher, S. 1988 Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77 (2), 439–471.Google Scholar
Simoni, D., Lengani, D., Ubaldi, M., Zunino, P. & Dellacasagrande, M. 2017 Inspection of the dynamic properties of laminar separation bubbles: free-stream turbulence intensity effects for different Reynolds numbers. Exp. Fluids 58 (6), 66.CrossRefGoogle Scholar
Souverein, L.J., Dupont, P., Debieve, J.-F., Dussauge, J.-P., Van Oudheusden, B.W. & Scarano, F. 2010 Effect of interaction strength on unsteadiness in shock-wave-induced separations. AIAA J. 48 (7), 1480–1493.CrossRefGoogle Scholar
Tanarro, Á., Vinuesa, R. & Schlatter, P. 2020 Effect of adverse pressure gradients on turbulent wing boundary layers. J. Fluid Mech. 883, A8.CrossRefGoogle Scholar
Teramoto, S. 2005 Large-eddy simulation of transitional boundary layer with impinging shock wave. AIAA J. 43 (11), 2354–2363.CrossRefGoogle Scholar
Theofilis, V., Hein, S. & Dallmann, U. 2000 On the origins of unsteadiness and three-dimensionality in a laminar separation bubble. Phil. Trans. R. Soc. Lond. A 358 (1777), 3229–3246.CrossRefGoogle Scholar
Tong, F., Li, X., Duan, Y. & Yu, C. 2017 Direct numerical simulation of supersonic turbulent boundary layer subjected to a curved compression ramp. Phys. Fluids 29 (12), 125101.CrossRefGoogle Scholar
Touber, E. & Sandham, N.D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.CrossRefGoogle Scholar
Trettel, A. & Larsson, J. 2016 Mean velocity scaling for compressible wall turbulence with heat transfer. Phys. Fluids 28 (2), 026102.Google Scholar
Unnikrishnan, S. & Gaitonde, D.V. 2020 Linear, nonlinear and transitional regimes of second-mode instability. J. Fluid Mech. 905, A25.CrossRefGoogle Scholar
Unnikrishnan, S. & Gaitonde, D.V. 2021 Perturbation analysis of nonlinear stages in hypersonic transition. Intl J. Comput. Fluid Dyn. 35 (5), 306–318.CrossRefGoogle Scholar
Valdivia, A., Yuceil, K.B., Wagner, J.L., Clemens, N.T. & Dolling, D.S. 2014 Control of supersonic inlet-isolator unstart using active and passive vortex generators. AIAA J. 52 (6), 1207–1218.CrossRefGoogle Scholar
Verma, S.B. & Manisankar, C. 2012 Shockwave/boundary-layer interaction control on a compression ramp using steady micro jets. AIAA J. 50 (12), 2753–2764.CrossRefGoogle Scholar
Vinokur, M. 1974 Conservation equations of gasdynamics in curvilinear coordinate systems. J. Comput. Phys. 14 (2), 105–125.CrossRefGoogle Scholar
Visbal, M. & Gaitonde, D. 1998 High-order accurate methods for unsteady vortical flows on curvilinear meshes. In 36th AIAA Aerospace Sciences Meeting and Exhibit, AIAA Paper 1998-0131.Google Scholar
Wagner, J.L., Yuceil, K.B., Valdivia, A., Clemens, N.T. & Dolling, D.S. 2009 Experimental investigation of unstart in an inlet/isolator model in mach 5 flow. AIAA J. 47 (6), 1528–1542.CrossRefGoogle Scholar
Watmuff, J.H. 1999 Evolution of a wave packet into vortex loops in a laminar separation bubble. J. Fluid Mech. 397, 119–169.CrossRefGoogle Scholar
Webb, N., Clifford, C. & Samimy, M. 2013 An investigation of the control mechanism of plasma actuators in a shock wave-boundary layer interaction. In 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA Paper 2013-402.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar
Yao, Y., Krishnan, L., Sandham, N.D. & Roberts, G.T. 2007 The effect of mach number on unstable disturbances in shock/boundary-layer interactions. Phys. Fluids 19 (5), 054104.CrossRefGoogle Scholar
Zhang, K., Sandham, N.D. & Hu, Z. 2018 Instability of supersonic ramp flow with intermittent transition to turbulence. In Direct and Large-Eddy Simulation X, pp. 373–378. Springer.CrossRefGoogle Scholar
Zhang, Y., Tan, H., Sun, S. & Rao, C. 2015 Control of cowl shock/boundary-layer interaction in hypersonic inlets by bump. AIAA J. 53 (11), 3492–3496.Google Scholar
Zhang, Y., Tan, H., Zhuang, Y. & Wang, D. 2014 Influence of expansion waves on cowl shock/boundary layer interaction in hypersonic inlets. J. Propul. Power 30 (5), 1183–1191.CrossRefGoogle Scholar