Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T02:06:28.921Z Has data issue: false hasContentIssue false
  • English
  • Français

First instability of the flow of shear-thinning and shear-thickening fluids past a circular cylinder

Published online by Cambridge University Press:  30 April 2012

Iman Lashgari ,
Jan O. Pralits ,
Flavio Giannetti  and
Luca Brandt
Iman Lashgari
Affiliation:
Linné Flow Centre, KTH Mechanics, S-100 44 Stockholm, Sweden
Jan O. Pralits
Affiliation:
DIIN, University of Salerno, via Ponte don Melillo, 84084 Fisciano (SA), Italy DICAT, University of Genova, via Montallegro 1, 16145 Genova, Italy
Flavio Giannetti
Affiliation:
DIIN, University of Salerno, via Ponte don Melillo, 84084 Fisciano (SA), Italy
Luca Brandt*
Affiliation:
Linné Flow Centre, KTH Mechanics, S-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The first bifurcation and the instability mechanisms of shear-thinning and shear-thickening fluids flowing past a circular cylinder are studied using linear theory and numerical simulations. Structural sensitivity analysis based on the idea of a ‘wavemaker’ is performed to identify the core of the instability. The shear-dependent viscosity is modelled by the Carreau model where the rheological parameters, i.e. 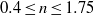the power-index and the material time constant, are chosen in the range and 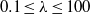. We show how shear-thinning/shear-thickening effects destabilize/stabilize the flow dramatically when scaling the problem with the reference zero-shear-rate viscosity. These variations are explained by modifications of the steady base flow due to the shear-dependent viscosity; the instability mechanisms are only slightly changed. The characteristics of the base flow, drag coefficient and size of recirculation bubble are presented to assess shear-thinning effects. We demonstrate that at critical conditions the local Reynolds number in the core of the instability is around 50 as for Newtonian fluids. The perturbation kinetic energy budget is also considered to examine the physical mechanism of the instability.

JFM classification

Instability: Instability Non-Newtonian Flows: Non-Newtonian Flows Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 701 , 25 June 2012 , pp. 201 - 227
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alizard, F., Robinet, J.-C. & Rist, U. 2010 Sensitivity analysis of a streamwise corner flow. Phys. Fluids 22 (1), 014103.CrossRefGoogle Scholar
2. Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
3. Bird, R. B., Curtiss, C. F., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids, 2nd edn. Wiley-Interscience.Google Scholar
4. Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.CrossRefGoogle Scholar
5. Brandt, L., Sipp, D., Pralits, J. O. & Marquet, O. 2011 Effect of base-flow variation on non-modal stability. J. Fluid Mech. 687, 503–528.CrossRefGoogle Scholar
6. Camarri, S. & Giannetti, F. 2007 On the inversion of the von Karman street in the wake of a confined square cylinder. J. Fluid Mech. 574, 169–178.CrossRefGoogle Scholar
7. Camarri, S. & Giannetti, F. 2010 Effect of confinement on three-dimensional stability in the wake of a circular cylinder. J. Fluid Mech. 642, 477–487.CrossRefGoogle Scholar
8. Caton, F. 2006 Linear stability of circular Couette flow of inelastic viscoplastic fluids. J. Non-Newtonian Fluid Mech. 134, 148–154.CrossRefGoogle Scholar
9. Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
10. Coelho, P. M. & Pinho, F. T. 2003a Vortex shedding in cylinder flow of shear-thinning fluids. I identification and demarcation of flow regimes. J. Non-Newtonian Fluid Mech. 110, 143–176.CrossRefGoogle Scholar
11. Coelho, P. M. & Pinho, F. T. 2003b Vortex shedding in cylinder flow of shear-thinning fluids. II flow characteristics. J. Non-Newtonian Fluid Mech. 110, 177–193.CrossRefGoogle Scholar
12. Coelho, P. M. & Pinho, F. T. 2004 Vortex shedding in cylinder flow of shear-thinning fluids. III pressure measurements. J. Non-Newtonian Fluid Mech. 121, 55–68.Google Scholar
13. Fischer, P. F. & Rønquist, E. M. 1994 Spectral element methods for large scale parallel Navier–Stokes calculations. Comput. Meth. Appl. Mech. Engng 116, 69–76.CrossRefGoogle Scholar
14. Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
15. Kunde, P. K. & Cohen, I. M. 1990 Fluid Mechanics. Elsevier.Google Scholar
16. Marquet, O., Lombardi, M., Chomaz, J.-M., Sipp, D. & Jacquin, L. 2009 Direct and adjoint global modes of a recirculation bubble: lift-up and convective non-normalities. J. Fluid Mech. 622, 1–21.CrossRefGoogle Scholar
17. Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
18. Meliga, P., Sipp, D. & Chomaz, J.-M. 2010a Effect of compressibility on the global stability of axisymmetric wake flows. J. Fluid Mech. 660, 499–526.CrossRefGoogle Scholar
19. Meliga, P., Sipp, D. & Chomaz, J.-M. 2010b Open-loop control of compressible afterbody flows using adjoint methods. Phys. Fluids 22 (5), 054109.CrossRefGoogle Scholar
20. Milleta, S., Rousset, F. & Hadid, V. B. H. B. 2009 Stability analysis of stratified coating flow of shear-thinning fluids. Eur. Phys. J. Special Topics 166, 143–146.CrossRefGoogle Scholar
21. Mossaz, S., Jay, P. & Magnin, A. 2010 Criteria for the appearance of recirculating and non-stationary regimes behind a cylinder in a viscoplastic fluid. J. Non-Newtonian Fluid Mech. 165, 1525–1535.CrossRefGoogle Scholar
22. Nejat, A., Abdollahi, V. & Vahidkhah, K. 2011 Lattice Boltzmann simulation of non-Newtonian flows past confined cylinders. J. Non-Newtonian Fluid Mech. 166, 689–697.CrossRefGoogle Scholar
23. Nouar, C., Bottaro, A. & Brancher, J. P. 2007 Delaying transition to turbulence in channel flow: revisiting the stability of shear-thinning fluids. J. Fluid Mech. 592, 177–194.CrossRefGoogle Scholar
24. Nouar, C. & Frigaard, I. 2009 Stability of plane Couette-Poiseuille flow of shear-thinning fluid. Phys. Fluids 21, 064104.CrossRefGoogle Scholar
25. Panda, S. K. & Chhabra, R. 2010 Laminar flow of power-law fluids past a rotating cylinder. J. Non-Newtonian Fluid 165, 1442–1461.CrossRefGoogle Scholar
26. Patera, A. T. 1984 A spectral element method for fluid dynamics: laminar flow in a channel expansion. J. Comput. Phys. 54, 468–488.CrossRefGoogle Scholar
27. Patnana, V. K., Bharti, R. P. & Chhabra, R. P. 2009 Two-dimensional unsteady flow of power-law fluids over a cylinder. Chem. Engng Sci. 64, 2978–2999.CrossRefGoogle Scholar
28. Pipe, C. J. & Monkewitz, P. A. 2006 Vortex shedding in flows of dilute polymer solutions. J. Non-Newtonian Fluid Mech. 139, 54–67.CrossRefGoogle Scholar
29. Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
30. Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard-von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
31. Richter, D., Iaccarino, G. & Shaqfeh, E. S. G. 2010 Simulations of three-dimensional viscoelastic flows past a circular cylinder at moderate Reynolds numbers. J. Fluid. Mech. 651, 415–442.CrossRefGoogle Scholar
32. Richter, D., Shaqfeh, E. S. G. & Iaccarino, G. 2011 Floquet stability analysis of viscoelastic flow over a cylinder. J. Non-Newtonian Fluid Mech. 166, 554–565.CrossRefGoogle Scholar
33. Sarpkaya, T., Rainey, P. G. & Kell, R. E. 1973 Flow of dilute polymer solution about circular cylinder. J. Fluid Mech. 57, 177–208.CrossRefGoogle Scholar
34. Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open flows: a linearized approach. Appl. Mech. Rev. 63, 030801.CrossRefGoogle Scholar
35. Sivakumar, P., Bharti, R. P. & Chhabra, R. 2006 Effect of power-law index on critical parameters for power-law flow across an unconfined circular cylinder. Chem. Engng Sci. 61, 6035–6046.CrossRefGoogle Scholar