Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T01:36:01.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Falling liquid films in narrow tubes: occlusion scenarios

Published online by Cambridge University Press:  05 May 2020

Georg F. Dietze Open the ORCID record for Georg F. Dietze [Opens in a new window] ,
G. Lavalle Open the ORCID record for G. Lavalle [Opens in a new window]  and
C. Ruyer-Quil
Georg F. Dietze*
Affiliation:
Université Paris-Saclay, CNRS, FAST, 91405 Orsay, France
G. Lavalle
Affiliation:
Université Paris-Saclay, CNRS, LIMSI, 91405 Orsay, France
C. Ruyer-Quil
Affiliation:
Université Savoie Mont Blanc, CNRS, LOCIE, 73376 Le Bourget du Lac, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

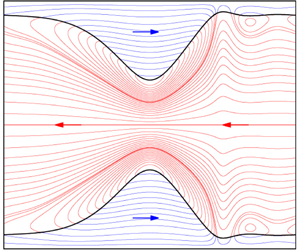
We study a gravity-driven wavy liquid film falling down the inner surface of a narrow cylindrical tube in the presence of an active core gas flow. We employ the model of Dietze and Ruyer-Quil (J. Fluid Mech., vol. 762, 2015, pp. 68–109) to investigate the role of surface waves in the occlusion of the tube. We consider four real working liquids and reproduce several experiments from the literature, focusing on conditions where the Bond number is greater or equal to unity. We prove that occlusion is triggered by spatially growing surface waves beyond the limit of saturated travelling-wave solutions, and delimit three possible regimes for a naturally evolving wavy film: (i) certain occlusion, when the liquid Reynolds number is greater than the limit of the spatially most amplified travelling waves. Occlusion is caused by surface waves emerging from linear wave selection (scenario I); (ii) conditional occlusion, when the most amplified waves possess travelling states but longer waves do not. Occlusion is triggered by secondary instability, generating long waves through nonlinear coarsening dynamics (scenario II); and (iii) impossible occlusion, when travelling waves always exist, no matter how great their wavelength. We show that certain occlusion is delayed by gravity and precipitated by a counter-current gas flow, axial viscous diffusion (high-viscosity liquids) and inertia (low-viscosity liquids). The latter two effects are also found to determine whether the occlusion mechanism is dictated by loss of travelling-wave solutions or absolute instability. Finally, we show that occlusion can be prevented through coherent inlet forcing. As a side benefit, we introduce an augmented version of our model based on a localized additional force term that allows representing stable travelling liquid pseudo-plugs.

JFM classification

Interfacial Flows (free surface): Thin films Interfacial Flows (free surface): Capillary flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 894 , 10 July 2020 , A17
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Institut de Mécanique des Fluides de Toulouse (IMFT) - Univ. de Toulouse, CNRS-INPT-UPS, Toulouse, France

References

Albert, C., Marschall, H. & Bothe, D. 2013 Direct numerical simulation of interfacial mass transfer into falling films. Intl J. Heat Mass Transfer 69, 343–357.CrossRefGoogle Scholar
Alekseenko, S. V., Aktershev, S. P., Cherdantsev, A. V., Kharlamov, S. M. & Markovich, D. M. 2009 Primary instabilities of liquid film flow sheared by turbulent gas stream. Intl J. Multiphase Flow 35, 617–627.CrossRefGoogle Scholar
Aul, R. W. & Olbricht, W. L. 1990 Stability of a thin annular film in pressure-driven, low-Reynolds-number flow through a capillary. J. Fluid Mech. 215, 585–599.CrossRefGoogle Scholar
Beltrame, P. 2018 Partial and complete wetting in a micro-tube. Europhys. Lett. 121, 64002.CrossRefGoogle Scholar
Benney, D. J. 1966 Long waves on liquid films. J. Math. Phys. 45, 150–155.CrossRefGoogle Scholar
Bian, S., Tai, C.-F., Halpern, D., Zheng, Y. & Grotberg, J. B. 2010 Experimental study of flow fields in an airway closure model. J. Fluid Mech. 647, 391–402.CrossRefGoogle Scholar
Brackbill, J. U., Kothe, D. B. & Zemach, C. 1992 A continuum method for modelling surface tension. J. Comput. Phys. 100, 335–354.CrossRefGoogle Scholar
Brooke Benjamin, T. 1957 Wave formation in laminar flow down an inclined plane. J. Fluid Mech. 2, 554–574.CrossRefGoogle Scholar
Camassa, R., Forest, M. G., Lee, L., Ogrosky, H. R. & Olander, J. 2012 Ring waves as a mass transport mechanism in air-driven core-annular flows. Phys. Rev. E 86 (6), 066305.Google ScholarPubMed
Camassa, R., Marzuola, J. L, Ogrosky, H. R. & Vaughn, N. 2016 Traveling waves for a model of gravity-driven film flows in cylindrical domains. Physica D 333, 254–265.Google Scholar
Camassa, R., Ogrosky, H. R. & Olander, J. 2014 Viscous film-flow coating the interior of a vertical tube. Part 1. Gravity-driven flow. J. Fluid Mech. 745, 682–715.CrossRefGoogle Scholar
Camassa, R., Ogrosky, H. R. & Olander, J. 2017 Viscous film-flow coating the interior of a vertical tube. Part 2. Air-driven flow. J. Fluid Mech. 825, 1056–1090.CrossRefGoogle Scholar
Chang, H. C., Demekhin, E. A. & Kalaidin, E. 1996a Simulation of noise-driven wave dynamics on a falling film. AIChE J. 42 (6), 1553–1568.CrossRefGoogle Scholar
Chang, H. C., Demekhin, E. A., Kalaidin, E. & Ye, Y. 1996b Coarsening dynamics of falling-film solitary waves. Phys. Rev. E 54 (2), 1467–1477.Google Scholar
Chang, H. C., Demekhin, E. A. & Kopelevich, D. I. 1993 Nonlinear evolution of waves on a vertically falling film. J. Fluid Mech. 250, 433–480.CrossRefGoogle Scholar
Dao, E. K. & Balakotaiah, V. 2000 Experimental study of wave occlusion on falling films in a vertical pipe. AIChE J. 46 (7), 1300–1306.CrossRefGoogle Scholar
Delaunay, C. 1841 Sur la surface de révolution dont la courbure moyenne est constante. J. Math. Pures Appl. 6, 309–320.Google Scholar
Dietze, G. F. 2016 On the Kapitza instability and the generation of capillary waves. J. Fluid Mech. 789, 368–401.CrossRefGoogle Scholar
Dietze, G. F. 2019 Effect of wall corrugations on scalar transfer to a wavy falling liquid film. J. Fluid Mech. 859, 1098–1128.CrossRefGoogle Scholar
Dietze, G. F. & Ruyer-Quil, C. 2013 Wavy liquid films in interaction with a confined laminar gas flow. J. Fluid Mech. 722, 348–393.CrossRefGoogle Scholar
Dietze, G. F. & Ruyer-Quil, C. 2015 Films in narrow tubes. J. Fluid Mech. 762, 68–109.CrossRefGoogle Scholar
Ding, Z., Liu, Z., Liu, R. & Yang, C. 2019 Thermocapillary effect on the dynamics of liquid films coating the interior surface of a tube. Intl J. Heat Mass Transfer 138, 524–533.CrossRefGoogle Scholar
Doedel, E. J. 2008 AUTO07p: Continuation and Bifurcation Software for Ordinary Differential Equations. Montreal Concordia University.Google Scholar
Duprat, C., Ruyer-Quil, C., Kalliadasis, S. & Giorgiutti-Dauphiné, F. 2007 Absolute and convective instabilities of a viscous film flowing down a vertical fiber. Phys. Rev. Lett. 98, 244502.CrossRefGoogle Scholar
Everett, D. H. & Haynes, J. M. 1972 Model studies of capillary condensation. J. Colloid Interface Sci. 38 (1), 125–137.CrossRefGoogle Scholar
Frenkel, A. L., Babchin, A. J., Levich, B. G., Shlang, T. & Sivashinsky, G. I. 1987 Annular flows can keep unstable films from breakup: nonlinear saturation of capillary instability. J. Colloid Interface Sci. 115 (1), 225–233.CrossRefGoogle Scholar
Gauglitz, P. A. & Radke, C. J. 1988 An extended evolution equation for liquid film breakup in cylindrical capillaries. Chem. Engng Sci. 43 (7), 1457–1465.CrossRefGoogle Scholar
Goren, S. L. 1962 The instability of an annular thread of fluid. J. Fluid Mech. 12 (2), 309–319.CrossRefGoogle Scholar
Grotberg, J. 2011 Respiratory fluid mechanics. Phys. Fluids 23, 021301.CrossRefGoogle ScholarPubMed
Hickox, C. E. 1971 Instability due to viscosity and density stratification in axisymmetric pipe flow. Phys. Fluids 14 (2), 251–262.CrossRefGoogle Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225.CrossRefGoogle Scholar
Jensen, O. E. 2000 Draining collars and lenses in liquid-lined vertical tubes. J. Colloid Interface Sci. 221, 38–49.CrossRefGoogle ScholarPubMed
Joseph, D. D., Chen, K. P. & Renardy, Y. Y. 1997 Core-annular flows. Annu. Rev. Fluid Mech. 29, 65–90.CrossRefGoogle Scholar
Kalliadasis, S. & Chang, H. C. 1994 Drop formation during coating of vertical fibres. J. Fluid Mech. 261, 135–168.CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2012 Falling Liquid Films, Applied Mathematical Sciences, vol. 176. Springer.CrossRefGoogle Scholar
Kamm, R. D. & Schroter, R. C. 1989 Is airway closure caused by a liquid film instability? Respir. Physiol. 75, 141–156.CrossRefGoogle ScholarPubMed
Kapitza, P. L. 1948 Wave flow of thin layer of viscous fluid (in Russian). Zh. Eksp. Teor. Fiz. 18 (1), 3–28.Google Scholar
King, M. & Macklem, P. T. 1977 Rheological properties of microliter quantities of normal mucus. J. Appl. Phys. 42 (6), 797–802.CrossRefGoogle ScholarPubMed
Kouris, C. & Tsamopoulos, J. 2001 Dynamics of axisymmetric core-annular flow in a straight tube. I. The more viscous fluid in the core, bamboo waves. Phys. Fluids 13 (4), 841–858.CrossRefGoogle Scholar
Lavalle, G., Grenier, N., Mergui, S. & Dietze, G. F. 2020 Solitary waves on superconfined falling liquid films. Phys. Rev. Fluids 5, 032001(R).CrossRefGoogle Scholar
Lewis, T. A., Tzeng, Y.-S., McKinstry, E. L., Tooker, A. C., Hong, K., Sun, Y., Mansour, J., Handler, Z. & Albert, M. S. 2005 Quantification of airway diameters and 3D airway tree rendering from dynamic hyperpolarized 3He magnetic resonance imaging. Magn. Reson. Med. 53, 474–478.CrossRefGoogle ScholarPubMed
Lister, J. R., Rallison, J. M., King, A. A., Cummings, L. J. & Jensen, O. E. 2006 Capillary drainage of an annular film: the dynamics of collars and lobes. J. Fluid Mech. 552, 311–343.CrossRefGoogle Scholar
Liu, J. & Gollub, J. P. 1993 Onset of spatially chaotic waves on flowing films. Phys. Rev. Lett. 70 (15), 2289–2292.CrossRefGoogle ScholarPubMed
Liu, R. & Ding, Z. 2017 Stability of viscous film flow coating the interior of a vertical tube with a porous wall. Phys. Rev. E 95 (5), 053101.Google ScholarPubMed
Mathematica 2014 Version 10.0.2.0. Wolfram Research, Inc.Google Scholar
Nosoko, T., Yoshimura, P. N., Nagata, T. & Oyakawa, K. 1996 Characteristics of two-dimensional waves on a falling liquid film. Chem. Engng Sci. 51 (5), 725–732.CrossRefGoogle Scholar
Plateau, J. P. 1849 Recherches expérimentales et théoriques sur les figures d’équilibre d’une masse liquide sans pesanteur. Mémoires de l’Académie Royale des Sciences, des Lettres et des Beaux-Arts de Belgique 23, 1–150.Google Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228, 5838–5866.CrossRefGoogle Scholar
Quéré, D. 1990 Thin films flowing on vertical fibers. Europhys. Lett. 13 (8), 721–726.CrossRefGoogle Scholar
Quéré, D. 1999 Fluid coating on a fibre. Annu. Rev. Fluid Mech. 31, 347–384.CrossRefGoogle Scholar
Rayleigh, Lord 1892 On the instability of cylindrical fluid surfaces. Phil. Mag. 34 (207), 177–180.CrossRefGoogle Scholar
Richard, G., Ruyer-Quil, C. & Vila, J. P. 2016 A three-equation model for thin films down an inclined plane. J. Fluid Mech. 804, 162–200.CrossRefGoogle Scholar
Seebauer, F., Poechlauer, P., Braune, S. & Steinhofer, S.2012 Tube bundle falling film microreactor for performing gas liquid reactions. US Patent 8221708B2.Google Scholar
Shkadov, V. Y. 1967 Wave flow regimes of a thin layer of viscous fluid subject to gravity. Fluid Dyn. 2 (1), 29–34.CrossRefGoogle Scholar
Suresh, V. & Grotberg, J. B. 2005 The effect of gravity on liquid plug propagation in a two-dimensional channel. Phys. Fluids 17 (3), 031507.CrossRefGoogle Scholar
Thiele, U., Velarde, M. G., Neuffer, K & Pomeau, Y. 2001 Sliding drops in the diffuse interface model coupled to hydrodynamics. Phys. Rev. E 64 (6), 061601.Google ScholarPubMed
Trifonov, Y. Y. 1992 Steady-state traveling waves on the surface of a viscous liquid film falling down on vertical wires and tubes. AIChE J. 38 (6), 821–834.CrossRefGoogle Scholar
Trifonov, Y. Y. 2010 Counter-current gas–liquid wavy film flow between the vertical plates analyzed using the Navier–Stokes equations. AIChE J. 56 (8), 1975–1987.Google Scholar
Tseluiko, D. & Kalliadasis, S. 2011 Nonlinear waves in counter-current gas–liquid film flow. J. Fluid Mech. 673, 19–59.CrossRefGoogle Scholar
Ubal, S., Campana, D. M., Giavedoni, M. D. & Saita, F. A. 2008 Stability of the steady-state displacement of a liquid plug driven by a constant pressure difference along a prewetted capillary tube. Ind. Engng Chem. Res. 47, 6307–6315.CrossRefGoogle Scholar
Vlachos, N. A., Paras, S. V., Mouza, A. A. & Karabelas, A. J. 2001 Visual observations of flooding in narrow rectangular channels. Intl J. Multiphase Flow 27, 1415–1430.CrossRefGoogle Scholar
Wray, A. W. 2013 Electrostatically controlled large-amplitude, non-axisymmetric waves in thin film flows down a cylinder. J. Fluid Mech. 736, R2.CrossRefGoogle Scholar
Xu, F. & Jensen, O. 2017 Trapping and displacement of liquid collars and plugs in rough-walled tubes. Phys. Rev. Fluids 2, 094004.CrossRefGoogle Scholar
Yih, C. S. 1963 Stability of liquid flow down an inclined plane. Phys. Fluids 6 (3), 321–334.CrossRefGoogle Scholar
Yoshimura, P. N., Nosoko, P. & Nagata, T. 1996 Enhancement of mass transfer into a falling laminar liquid film by two-dimensional surface waves—some experimental observations and modeling. Chem. Engng Sci. 51 (8), 1231–1240.CrossRefGoogle Scholar
Zapke, A. & Kröger, D. G. 2000 Countercurrent gas–liquid flow in inclined and vertical ducts – I: flow patterns, pressure drop characteristics and flooding. Intl J. Multiphase Flow 26, 1439–1455.CrossRefGoogle Scholar
Zhou, Z.-Q., Peng, J., Zhang, Y.-J. & Zhuge, W.-L. 2016 Viscoelastic liquid film flowing down a flexible tube. J. Fluid Mech. 802, 583–610.CrossRefGoogle Scholar

Dietz et al. supplementary movie 1

Spatiotemporal computation from panel 3c, corresponding to experiment in panel 3c of Camassa et al. (J. Fluid Mech., vol. 745, 2014, pp. 682-715). Case 1, Re=4.5E-4. Occlusion mechanism: surface waves grow spatially until their height attains the tube axis, whereupon individual gas bubbles are pinched off.

Download Dietz et al. supplementary movie 1(Video)
Video 7.8 MB

Dietz et al. supplementary movie 2

Spatiotemporal computation from panel 15c, corresponding to experimental run 20 in Dao and Balakotaiah (AIChE J., vol. 7, 2000, pp. 1300). Regime of certain occlusion: case 2, Re=0.0497. Scenario I: Occlusion is caused by spatially most amplified waves emerging from linear wave selection.

Download Dietz et al. supplementary movie 2(Video)
Video 6.5 MB

Dietz et al. supplementary movie 3

Spatiotemporal computation from panel 15d, corresponding to experimental run 13 in Dao and Balakotaiah (AIChE J., vol. 7, 2000, pp. 1300). Regime of conditional occlusion: case 3, Re=0.258. Scenario II: Occlusion is caused by wave coalescence due to secondary instability of the regular wave train emerging from linear wave selection.

Download Dietz et al. supplementary movie 3(Video)
Video 3.4 MB

Dietz et al. supplementary movie 4

Spatiotemporal computation from panel 16a. Regime of conditional occlusion: case 3, Re=0.14. The occlusion point is shifted greatly downstream compared to panel 15d (movie M3).

Download Dietz et al. supplementary movie 4(Video)
Video 7.1 MB