Article contents
Explosive dispersal of granular media
Published online by Cambridge University Press: 17 March 2023
Abstract
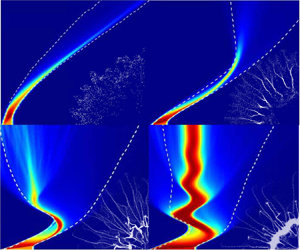
Explosive dispersal of granular media widely occurs in nature across various length scales, also enabling engineering applications ranging from commercial or military explosive systems to the loss prevention industry. However, the complex particle–flow coupling makes the explosive dispersal behaviour of particles difficult to control or even characterize. Here, we study the central explosion-driven dispersal of dense particle layers using the coarse-grained computational fluid dynamics–discrete element method and present a comprehensive investigation of both macroscale dispersal behaviours and particle-scale pattern formation. Employing three independent dimensionless parameters that characterize the efficiency, homogeneity and completeness of explosive dispersal, we categorize the dispersal behaviours into ideal, partial, retarded and failed modes, and propose the corresponding thresholds. As the mass ratio of granular materials to central pressurized gases (M/C) spans four orders of magnitude, the dispersal mode transitions from ideal to partial, then to retarded and finally to failed mode. The transitions of dispersal modes correspond to the particle–flow coupling regime crossovers, which change from decoupling to weak, medium and finally to strong coupling as the dispersal mode undergoes corresponding transitions. We proceed to develop continuum models accounting for the shock compaction and the ensuing pulsation of the particle ring that are capable of identifying the ideal dispersal mode from various dispersal systems. We also provide insights into the origins of diverse particle-scale patterns that are strongly correlated with macroscale dispersal modes and critical for the accurate prediction of dispersal modes.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 6
- Cited by



