Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-21T12:51:10.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Exploring the phase diagram of fully turbulent Taylor–Couette flow

Published online by Cambridge University Press:  18 November 2014

Rodolfo Ostilla-Mónico ,
Erwin P. van der Poel ,
Roberto Verzicco ,
Siegfried Grossmann  and
Detlef Lohse
Rodolfo Ostilla-Mónico*
Affiliation:
Physics of Fluids group, Department of Science and Technology, Mesa+ Institute and J.M. Burgers Centre of Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Erwin P. van der Poel
Affiliation:
Physics of Fluids group, Department of Science and Technology, Mesa+ Institute and J.M. Burgers Centre of Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Roberto Verzicco
Affiliation:
Physics of Fluids group, Department of Science and Technology, Mesa+ Institute and J.M. Burgers Centre of Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands Dipartimento di Ingegneria Industriale, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Roma 00133, Italy
Siegfried Grossmann
Affiliation:
Department of Physics, University of Marburg, Renthof 6, D-35032 Marburg, Germany
Detlef Lohse
Affiliation:
Physics of Fluids group, Department of Science and Technology, Mesa+ Institute and J.M. Burgers Centre of Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

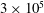Direct numerical simulations of Taylor–Couette flow, i.e. the flow between two coaxial and independently rotating cylinders, were performed. Shear Reynolds numbers of up to $3\times 10^{5}$, corresponding to Taylor numbers of 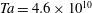$\mathit{Ta}=4.6\times 10^{10}$, were reached. Effective scaling laws for the torque are presented. The transition to the ultimate regime, in which asymptotic scaling laws (with logarithmic corrections) for the torque are expected to hold up to arbitrarily high driving, is analysed for different radius ratios, different aspect ratios and different rotation ratios. It is shown that the transition is approximately independent of the aspect and rotation ratios, but depends significantly on the radius ratio. We furthermore calculate the local angular velocity profiles and visualize different flow regimes that depend both on the shearing of the flow, and the Coriolis force originating from the outer cylinder rotation. Two main regimes are distinguished, based on the magnitude of the Coriolis force, namely the co-rotating and weakly counter-rotating regime dominated by Rayleigh-unstable regions, and the strongly counter-rotating regime where a mixture of Rayleigh-stable and Rayleigh-unstable regions exist. Furthermore, an analogy between radius ratio and outer-cylinder rotation is revealed, namely that smaller gaps behave like a wider gap with co-rotating cylinders, and that wider gaps behave like smaller gaps with weakly counter-rotating cylinders. Finally, the effect of the aspect ratio on the effective torque versus Taylor number scaling is analysed and it is shown that different branches of the torque-versus-Taylor relationships associated to different aspect ratios are found to cross within 15 % of the Reynolds number associated to the transition to the ultimate regime. The paper culminates in phase diagram in the inner versus outer Reynolds number parameter space and in the Taylor versus inverse Rossby number parameter space, which can be seen as the extension of the Andereck et al. (J. Fluid Mech., vol. 164, 1986, pp. 155–183) phase diagram towards the ultimate regime.

JFM classification

Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 761 , 25 December 2014 , pp. 1 - 26
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., He, X., Funfschilling, D. & Bodenschatz, E. 2012 Heat transport by turbulent Rayleigh–Bénard convection for $Pr=0.8$ and $3\times 10^{12}\lesssim Ra\lesssim 10^{15}$ : aspect ratio ${\rm\Gamma}=0.50$ . New J. Phys. 14, 103012.Google Scholar
Andereck, C. D., Dickman, R. & Swinney, H. L. 1983 New flows in a circular Couette system with corotating cylinders. Phys. Fluids 26 (1395).Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.Google Scholar
Benjamin, T. B. 1978 Bifurcation phenomena in steady flows of a viscous liquid. Proc. R. Soc. Lond. A 359, 1–43.Google Scholar
Brauckmann, H. & Eckhardt, B. 2013a Direct numerical simulations of local and global torque in Taylor–Couette Flow up to $\mathit{Re}=30.000$ . J. Fluid Mech. 718, 398–427.Google Scholar
Brauckmann, H. J. & Eckhardt, B. 2013b Intermittent boundary layers and torque maxima in Taylor–Couette flow. Phys. Rev. E 87 (3), 033004.CrossRefGoogle Scholar
Couette, M. 1890 Études sur le frottement des liquides. Gauthier-Villars et fils.Google Scholar
Donnelly, R. 1991 Taylor–Couette flow: the early days. Phys. Today 32–39.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
van Gils, D. P. M., Huisman, S. G., Bruggert, G. W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counter-rotating cylinders. Phys. Rev. Lett. 106, 024502.Google Scholar
van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118–149.Google Scholar
Görtler, H. 1940a Über den Einflusss der Wandkrümmung auf die Entstehung der Turbulenz. Z. Angew. Math. Mech. 20, 138–147.CrossRefGoogle Scholar
Görtler, H. 1940b Über eine dreidimensionale Instabilität laminarer Grenzschichten an konkaven Wänden. Z. Angew. Math. Mech. 21, 250–252.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.Google Scholar
Grossmann, S., Lohse, D. & Sun, C. 2014 Velocity profiles in strongly turbulent Taylor–Couette flow. Phys. Fluids 26, 025114.CrossRefGoogle Scholar
He, X., Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2012a Heat transport by turbulent Rayleigh–Bénard convection for $Pr=0.8$ and $4\times 10^{11}\lesssim Ra\lesssim 2\times 10^{14}$ : ultimate-state transition for aspect ratio ${\rm\Gamma}=100$ . New J. Phys. 14 (6), 063030.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012b Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
Hoffmann, P. H., Muck, K. C. & Bradshaw, P. 1985 The effect of concave surface curvature on turbulent boundary layers. J. Fluid Mech. 161, 371–403.CrossRefGoogle Scholar
Huisman, S. G., van Gils, D. P. M., Grossmann, S., Sun, C. & Lohse, D. 2012 Ultimate turbulent Taylor–Couette flow. Phys. Rev. Lett. 108, 024501.CrossRefGoogle ScholarPubMed
Huisman, S. G., Scharnowski, S., Cierpka, C., Kähler, C., Lohse, D. & Sun, C. 2013 Logarithmic boundary layers in strong Taylor–Couette turbulence. Phys. Rev. Lett. 110, 264501.CrossRefGoogle ScholarPubMed
Huisman, S. G., van der Veen, R. C. A., Sun, C. & Lohse, D. 2014 Multiple states in ultimate Taylor–Couette turbulence. Nature Commun. 5, 3820.CrossRefGoogle Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbritrary Prandtl number. Phys. Fluids 5, 1374–1389.CrossRefGoogle Scholar
Lathrop, D. P., Fineberg, Jay & Swinney, H. S. 1992a Transition to shear-driven turbulence in Couette–Taylor flow. Phys. Rev. A 46, 6390–6405.CrossRefGoogle ScholarPubMed
Lathrop, D. P., Fineberg, Jay & Swinney, H. S. 1992b Turbulent flow between concentric rotating cylinders at large Reynolds numbers. Phys. Rev. Lett. 68, 1515–1518.Google Scholar
Lewis, G. S. & Swinney, H. L. 1999 Velocity structure functions, scaling, and transitions in high-Reynolds-number Couette–Taylor flow. Phys. Rev. E 59, 5457–5467.CrossRefGoogle ScholarPubMed
Malkus, M. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Mallock, A. 1896 Experiments on fluid viscosity. Phil. Trans. R. Soc. Lond. A 187, 41–56.Google Scholar
Manna, M. & Vacca, A. 2009 Torque reduction in Taylor–Couette flows subject to an axial pressure gradient. J. Fluid Mech. 639, 373–401.Google Scholar
Martinez-Arias, B., Peixinho, J., Crumeyrolle, O. & Mutabazi, I. 2014 Effect of the number of vortices on the torque scaling in Taylor–Couette flow. J. Fluid Mech. 748, 756–767.Google Scholar
Merbold, S., Brauckmann, H. & Egbers, C. 2013 Torque measurements and numerical determination in differentially rotating wide gap Taylor–Couette flow. Phys. Rev. E 87, 023014.CrossRefGoogle ScholarPubMed
Muck, K. C., Hoffmann, P. H. & Bradshaw, P. 1985 The effect of convex surface curvature on turbulent boundary layers. J. Fluid Mech. 161, 347–369.CrossRefGoogle Scholar
Ostilla-Mónico, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Ostilla-Mónico, R., Huisman, S. G., Jannink, T. J. G., van Gils, D. P. M., Verzicco, R., Grossmann, S., Sun, C. & Lohse, D. 2014a Optimal Taylor–Couette flow: radius ratio dependence. J. Fluid Mech. 747, 1–29.CrossRefGoogle Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014b Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids 26, 015114.Google Scholar
Ostilla-Mónico, R., Verzicco, R., Grossmann, S. & Lohse, D. 2014c Turbulence decay towards the linearly-stable regime of Taylor–Couette flow. J. Fluid Mech. 747, 1–29.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Prandtl, L. 1933 Neuere ergebnisse der turbulenzforschung. Z. Verein. Deutsch. Ing. 77 (5), 105–114.Google Scholar
Ravelet, F., Delfos, R. & Westerweel, J. 2010 Influence of global rotation and Reynolds number on the large-scale features of a turbulent Taylor–Couette flow. Phys. Fluids 22 (5), 055103.Google Scholar
Roche, P. E., Gauthier, G., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12, 085014.Google Scholar
Spiegel, E. A. 1971 Convection in stars. Annu. Rev. Astron. Astrophys. 9, 323–352.Google Scholar
Taylor, G. I. 1923 Experiments on the motion of solid bodies in rotating fluids. Proc. R. Soc. Lond. A 104, 213–218.Google Scholar
Taylor, G. I. 1936 Fluid friction between rotating cylinders. II. Distribution of velocity between concentric cylinders when outer one is rotating and inner one is at rest. Proc. R. Soc. Lond. A 157, 565–578.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flow in cylindrical coordinates. J. Comput. Phys. 123, 402–413.Google Scholar
Wendt, F. 1933 Turbulente Strömungen zwischen zwei rotierenden Zylindern. Ingenieurs-Archiv 4, 577–595.Google Scholar