Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-08T22:15:02.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Experiments on the periodic oscillation of free containers driven by liquid sloshing

Published online by Cambridge University Press:  06 January 2012

Andrzej Herczyński  and
Patrick D. Weidman
Andrzej Herczyński
Affiliation:
Department of Physics, Boston College, Chestnut Hill, MA 02467-3811, USA
Patrick D. Weidman*
Affiliation:
Department of Mechanical Engineering, University of Colorado, Boulder, CO 80309-0427, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

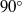Experiments on the time-periodic liquid sloshing-induced sideways motion of containers are presented. The measurements are compared with finite-depth potential theory developed from standard normal mode representations for rectangular boxes, upright cylinders, wedges and cones of apex angles, and cylindrical annuli. It is assumed that the rectilinear horizontal motion of the containers is frictionless. The study focuses on measurements of the horizontal oscillations of these containers arising solely from the liquid waves excited within. While the wedge and cone exhibit only one mode of oscillation, the boxes, cylinders and annuli have an infinite number of modes. For the boxes, cylinders and one of the annuli, we have been able to excite motion and record data for both the first and second modes of oscillation. Frequencies 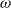were acquired as the average of three experimental determinations for every filling of mass 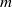in the dry containers of mass 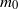. Measurements of the dimensionless frequencies 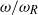over a range of dimensionless liquid masses 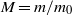are found to be in essential agreement with theoretical predictions. The frequencies 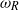used for normalization arise naturally in the mathematical analysis, different for each geometry considered. Free surface waveforms for a box, a cylinder, the wedge and the cone are compared at a fixed value of .

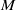JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave-structure interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 693 , 25 February 2012 , pp. 216 - 242
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abramowitz, M. & Stegun, I. 1972 Handbook of Mathematical Functions. U.S. Government Printing Office.Google Scholar
2. Abramson, H. N. 1966 The dynamical behaviour of liquids in a moving container. Tech. Rep. SP-106. NASA, Washington, DC.Google Scholar
3. Abramson, H. N., Chu, W.-H. & Ransleben, G. E. Jr. 1961 Representation of fuel sloshing in cylindrical tanks by an equivalent mechanical model. Am. Rocket Soc. J. 31, 1697–1705.Google Scholar
4. Ardakani, H. A. & Bridges, T. J. 2010 Dynamic coupling between shallow-water sloshing and horizontal vehicle motion. Eur. J. Appl. Maths 21, 479–517.CrossRefGoogle Scholar
5. Bauer, H. F. 1960 Theory of fluid oscillations in a circular ring tank partially filled with liquid. NASA TN-D-557.Google Scholar
6. Campbell, I. J. 1953 Wave motion in an annular tank. Phil. Mag. 44, 845–853.CrossRefGoogle Scholar
7. Cooker, M. J. 1994 Waves in a suspended container. Wave Motion 20, 385–395.CrossRefGoogle Scholar
8. Cooker, M. J. 1996 Wave energy losses from a suspended container. Phys. Fluids 8, 283–284.CrossRefGoogle Scholar
9. Davis, A. M. J. & Weidman, P. D. 2000 Asymptotic estimates for two-dimensional sloshing modes. Phys. Fluids 12, 971–978.CrossRefGoogle Scholar
10. Dodge, F. T. 2000 The new dynamical behaviour of liquids in moving containers. Southwest Research Institute, San Antonio, TX.Google Scholar
11. Faltinsen, O. M. & Timokha, A. N. 2009 Sloshing. Cambridge University Press.Google Scholar
12. Feddema, J., Dohrmann, C., Parker, G., Robinett, R., Romero, V. & Schmitt, D. 1996 Robotically controlled slosh-free motion of an open container of liquid. IEEE Proceedings, International Conference on Robotics and Automation, Minneapolis, MN, pp. 596–602. University of Colorado.CrossRefGoogle Scholar
13. Haberman, W. L., Jarski, E. J. & John, J. E. A. 1974 A note on the sloshing motion in a triangular tank. Z. Angew. Math. Phys. 25, 292–293.CrossRefGoogle Scholar
14. Herczynski, A. & Weidman, P. D. 2009 Synchronous sloshing in a free container. APS Division of Fluid Dynamics, 62nd Annual Meeting, Minneapolis, MN, 22–24 November.Google Scholar
15. Ibrahim, R. A. 2005 Liquid Sloshing Dynamics: Theory and Applications. Cambridge University Press.CrossRefGoogle Scholar
16. Keulegan, G. H. 1959 Energy dissipation in standing waves in rectangular basins. J. Fluid Mech. 6, 33–50.CrossRefGoogle Scholar
17. Lamb, H. 1932 Hydrodynamics, 5th edn. Cambridge University Press.Google Scholar
18. Maxworthy, T. 1976 Experiments on collisions between solitary waves. J. Fluid Mech. 76, 177–185.CrossRefGoogle Scholar
19. Moiseev, N. N. 1953 The problem of solid objects containing liquids with a free surface. Mat. Sbornik. 32(74) (1), 61–96.Google Scholar
20. Moiseev, N. N. 1964 Introduction to the theory of oscillations of liquid-containing bodies. Adv. Appl. Mech. 8, 233–289.CrossRefGoogle Scholar
21. Sano, K. 1913 On seiches of Lake Toya. Proc. Tokyo Math. Phys. Soc. (2) 7, 17–22.Google Scholar
22. Seubert, C. R. & Schaub, H. 2010 Closed-loop charged relative motion experiments simulating constrained orbital motion. J. Guid. Control Dyn. 33, 1856–1865.CrossRefGoogle Scholar
23. Weidman, P. D. 1994 Synchronous sloshing in free and suspended containers. APS Division of Fluid Dynamics, 47th Annual Meeting, Atlanta, GA, 20–22 November.Google Scholar
24. Weidman, P. D. 2005 Sloshing in suspended containers. APS Division of Fluid Dynamics, 58th Annual Meeting, Chicago, IL, 20–22 November.Google Scholar
25. Wolfram, S. 1991 Mathematica: A System for Doing Mathematics by Computer, 2nd edn. Addison-Wesley.Google Scholar
26. Yu, J. 2010 Effects of finite depth on natural frequencies of suspended water tanks. Stud. Appl. Maths 125, 373–391.CrossRefGoogle Scholar