Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T23:19:26.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Experiments on mixing in wakes in shallow water

Published online by Cambridge University Press:  09 September 2016

Gioacchino Cafiero  and
Andrew W. Woods
Gioacchino Cafiero
Affiliation:
BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK Department of Industrial Engineering, Experimental Thermo-Fluid dynamics division, University of Naples, Via Claudio 21, 80125, Italy
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report on a series of laboratory experiments in which we investigate the mixing in a wake produced downstream of an obstacle in a uniform flow. The fluid is confined within a channel of finite width, and the water depth is small compared with the channel width. The mixing appears to be dominated by dispersion caused by the circulation of the eddies that are shed alternately from each side of the obstacle. However, due to bottom friction, these eddies gradually dissipate downstream. In turn, the intensity of the cross-stream mixing of the tracer decays in the downstream direction, limiting the cross-stream extent of the tracer. We present a time-averaged picture of the experiments which illustrates the deviation of the time-averaged flow in the wake relative to the uniform flow upstream. We then develop a time-averaged model for the flow, using mixing length theory to account for the cross-channel momentum transfer as an eddy viscosity 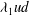$\unicode[STIX]{x1D706}_{1}ud$, where 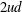$2ud$ is the cross-channel integral of the perturbation in the along-channel speed associated with the wake. We also include a frictional stress to account for the bottom friction. The model predicts a similar pattern of variation of the along-channel velocity in both the along- and cross-channel directions to our experimental data. By matching the cross-channel data with the model, we find that the constant 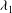$\unicode[STIX]{x1D706}_{1}$ has value 0.2. We also analyse our experimental data to develop a time-dependent picture of the mixing of a stream of dye released into the wake. Using the model for the evolution of the flow, we develop a model for the time-averaged mixing, again based on mixing length theory. The model predicts a similar spatial distribution for the tracer in both the cross-stream and along-stream directions to that seen in our experimental data. By quantitative comparison of the model with the data, we find that the best fit of the empirical eddy diffusivity, 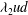$\unicode[STIX]{x1D706}_{2}ud$, with the data occurs with 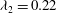$\unicode[STIX]{x1D706}_{2}=0.22$. We discuss implications of our results for modelling cross-stream mixing in shallow turbulent flow.

JFM classification

Mixing: Mixing Mixing: Turbulent mixing Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 351 - 369
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Breidenthal, R. 1981 Structure in turbulent mixing layers and wakes using a chemical reaction. J. Fluid Mech. 109, 1–24.Google Scholar
Cafiero, G., Discetti, S. & Astarita, T. 2014 Heat transfer enhancement of impinging jets with fractal generated turbulence. Intl J. Heat Mass Transfer 75, 173–183.Google Scholar
Cafiero, G., Discetti, S. & Astarita, T. 2015 Flow field topology of submerged jets with fractal generated turbulence. Phys. Fluids 27, 115103.Google Scholar
Cafiero, G., Greco, C. S., Astarita, T. & Discetti, S. 2016 Flow field features of impinging jets at short nozzle to plate distances. Exp. Therm. Fluid Sci. 78, 334–344.Google Scholar
van Carmer, C. F., Rummel, A. C. & Jirka, G. H. 2009 Mass transport in shallow turbulent wake flow by planar concentration analysis technique. J. Hydraul. Engng 135, 257–270.Google Scholar
Cenedese, C. & Dalziel, S. B. 1998 Concentration and depth fields determined by the light trasmitted through a dyed solution. In Proceedings of the 8th Symposium on Flow Visualization (ed. Carlomagno, G. M. & Grant, I.). ISBN 0 9533991 0 9, paper 061.Google Scholar
Chen, D. & Jirka, G. H. 1995 Experimental study of plane turbulent wakes in a shallow water layer. Fluid Dyn. Res. 16, 11–41.Google Scholar
Chen, D. & Jirka, G. H. 1997 Absolute and convective instabilities of plane turbulent wakes in a shallow water layer. J. Fluid Mech. 338, 157–172.Google Scholar
Chen, J., Li, D., Chen, B., Hu, F., Zhu, H. & Liu, C. 1999 The processes of dynamic sedimentation in the Changjiang Estuary. J. Sea Res. 41, 129–140.Google Scholar
Dairay, T., Obligado, M. & Vassilicos, J. C. 2015 Non-equilibrium scaling laws in axisymmetric turbulent wakes. J. Fluid Mech. 781, 166–195.Google Scholar
Garret, C. & Cummins, P. 2007 The efficiency of a tidal turbine in a channel. J. Fluid Mech. 588, 243–251.Google Scholar
Garret, C. & Cummins, P. 2013 Maximum power extraction from a turbine farm in shallow water. J. Fluid Mech. 714, 634–643.Google Scholar
Gartshore, I. S. 1967 Two-dimensional turbulent wakes. J. Fluid Mech. 30, 547–560.Google Scholar
Gill, A. E. 1981 Atmosphere–Ocean Dynamics. Academic.Google Scholar
Landel, J., Caulfield, C. & Woods, A. W. 2012 Streamwise dispersion and mixing in quasi-two-dimensional steady turbulent jets. J. Fluid Mech. 711, 212–258.Google Scholar
Lind, S. J., Stansby, P. K., Rogers, B. D. & Lloyd, P. M. 2015 Numerical predictions of water–air wave slam using incompressible–compressible smoothed particle hydrodynamics. Appl. Ocean Res. 49, 57–71.Google Scholar
Mingotti, N. & Woods, A. W. 2016 On turbulent particle fountains. J. Fluid Mech. 793, R1.Google Scholar
Moody, L. F. 1944 Friction factors for pipe flow. Trans. ASME 66, 671–684.Google Scholar
Mullyadzhanov, R., Ilyushin, B. & Hanjalic, K. 2015 On dynamics and secondary currents in meandering confined turbulent shallow jet. Intl J. Heat Fluid Flow 56, 284–289.Google Scholar
Negretti, M. E., Vignoli, G., Tubino, M. & Brocchini, M. 2006 Shallow-water wakes: an analytical study. J. Fluid Mech. 567, 457–475.Google Scholar
Nishino, T. & Willden, R. H. 2012 The efficiency of an array of tidal turbines partially blocking a wide channel. J. Fluid Mech. 708, 596–606.Google Scholar
Prandtl, L. 1925 Bericht über Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech. 5, 136–139.Google Scholar
Rocco, S. & Woods, A. W. 2015 Dispersion in two-dimensional buoyant plumes. J. Fluid Mech. 774, R1.Google Scholar
Seol, D. G. & Jirka, G. H. 2003 Quasi-two-dimensional properties of a single shallow-water vortex with high initial Reynolds numbers. J. Fluid Mech. 665, 274–299.CrossRefGoogle Scholar
Stansby, P. K. 2003 A mixing-length model for shallow turbulent wakes. J. Fluid Mech. 495, 369–384.Google Scholar
Stansby, P. K. 2006 Limitations of depth-averaged modeling for shallow wakes. J. Hydraul. Engng 132, 737–740.Google Scholar
Taylor, G. I. 1954 The dispersion of matter in a turbulent flow through a pipe. Proc. R. Soc. Lond. A 223 (1155), 446–468.Google Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar