Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-20T17:18:56.345Z Has data issue: false hasContentIssue false
  • English
  • Français

Experiments on gas transfer at the air–water interface induced by oscillating grid turbulence

Published online by Cambridge University Press:  14 December 2007

HERLINA  and
G. H. JIRKA
HERLINA
Affiliation:
Institute for Hydromechanics, University of Karlsruhe, Germany
G. H. JIRKA
Affiliation:
Institute for Hydromechanics, University of Karlsruhe, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

The gas transfer process across the air–water interface in a turbulent flow environment, with the turbulence generated in the water phase far away from the surface, was experimentally investigated for varying turbulent Reynolds numbers ReT ranging between 260 and 780. The experiments were performed in a grid-stirred tank using a combined particle image velocimetry – laser induced fluorescence (PIV-LIF) technique, which enables synoptic measurements of two-dimensional velocity and dissolved gas concentration fields. The visualization of the velocity and concentration fields provided direct insight into the gas transfer mechanisms. The high data resolution allowed detailed quantification of the gas concentration distribution (i.e. mean and turbulent fluctuation characteristics) within the thin aqueous boundary layer as well as revealing the near-surface hydrodynamics. The normalized concentration profiles show that as ReT increases, the rate of concentration decay into the bulk becomes slower. Independent benchmark data for the transfer velocity KL were obtained and their normalized values (KLSc0.5/uHT) depend on ReT with exponent −0.25. The spectra of the covariance term c′ w′ indicate that the contribution of c′ w′ is larger in the lower-frequency region for cases with small ReT, whereas for the other cases with higher ReT, the contribution of c′ w′ appears to be larger in the higher-frequency region (small eddies). These interrelated facts suggest that the gas transfer process is controlled by a spectrum of different eddy sizes and the gas transfer at different turbulence levels can be associated with certain dominant eddy sizes. The normalized mean turbulent flux 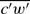profiles increase from around 0 at the interface to about 1 within a depth of approximately 2δe, where δe is the thickness of the gas boundary layer. The measured turbulent flux (c′ w′) is of the same order as the total flux (j), which shows that the contribution of c′ w′ to the total flux is significant.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 594 , 10 January 2008 , pp. 183 - 208
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Atmane, M. A. & George, J. 2002 Gas transfer across a zero-shear surface: a local approach. Geophysical Monograph 127, Gas Transfer at Water Surfaces, pp. 255–259.Google Scholar
Banerjee, S., Rhodes, E. & Scott, D. S. 1968 Mass transfer to falling wavy liquid films in turbulent flow. Indust. Engng Chem. Fund. 7, 22.CrossRefGoogle Scholar
Banerjee, S., Lakehal, D. & Fulgosi, M. 2004 Surface divergence model for scalar exchange between turbulent streams. Intl J. Multiphase Flow 30, 963–977.CrossRefGoogle Scholar
Batchelor, G. K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids 12 (12), 233–239.CrossRefGoogle Scholar
Brumley, B. 1984 Turbulence measurements near the free surface in stirred grid experiments. Gas Transfer at Water Surfaces, pp. 83–92.Google Scholar
Brumley, B. H. & Jirka, G. H. 1987 Near-surface turbulence in a grid-stirred tank. J. Fluid Mech. 183, 236–263.CrossRefGoogle Scholar
Brumley, B. H. & Jirka, G. H. 1988 Air–water transfer of slightly soluble gases: turbulence interfacial processes and conceptual models. PhysicoChem. Hydrodyn. 10, 295–319.Google Scholar
Chu, C. R. & Jirka, G. H. 1992 Turbulent gas flux measurements below the air–water interface of a grid-stirred tank. Intl J. Heat Mass Transfer 35, 1957–1968.Google Scholar
Churchill, M. A. 1961 Effect of water temperature on stream reaeration. J. Sanitary Engng Div. 5 (87), 59–71.Google Scholar
Danckwerts, P. V. 1951 Significance of liquid-film coefficients in gas absorption. Indust. Engng Chem. 43, 1460–1467.CrossRefGoogle Scholar
Donelan, M. A. & Wanninkhof, R. 2002 Gas transfer at water surfaces–concepts and issues. Geophysical Monograph 127, Gas Transfer at Water Surfaces, pp. 1–10.Google Scholar
Fortescue, G. E. & Pearson, J. R. 1967 On gas absorption into a turbulent liquid. Chem. Engng Sci. 22, 187–216.CrossRefGoogle Scholar
Gulliver, J. S. & Halverson, M. J. 1989 Air–water gas transfer in open channels. Water Resour. Res. 25, 1783–1793.CrossRefGoogle Scholar
Harriott, P. 1962 A random eddy modification of the penetration theory. Chem. Engng Sci. 17, 149–154.CrossRefGoogle Scholar
Herlina, 2005 Gas transfer at the air–water interface in a turbulent flow environment. Doctoral thesis, Inst. Hydromech. University of Karlsruhe, University Press ISBN 3-937300-74-0.Google Scholar
Herlina, & Jirka, G. H. 2004 Application of LIF to investigate gas transfer near the air–water interface in a grid-stirred tank. Exps Fluids 37, 341–349.CrossRefGoogle Scholar
Higbie, R. 1935 The rate of absorption of a pure gas into a still liquid during short periods of exposure. AIChE Trans. 31, 365–390.Google Scholar
Hopfinger, E. J. & Toly, J. A. 1976 Spatially decaying turbulence and its relation to mixing across density interfaces. J. Fluid Mech. 78, 155–175.CrossRefGoogle Scholar
Hunt, J. C. R. & Graham, J. M. R. 1978 Free-stream turbulence near plane boundaries. J. Fluid Mech. 84, 209–235.CrossRefGoogle Scholar
Jähne, B. & Haussecker, H. 1998 Air–water gas exchange. Annu. Rev. Fluid Mech. 30, 443–468.CrossRefGoogle Scholar
Jirka, G. H. & Ho, A. H. W. 1990 Measurements of gas concentration fluctuations at water surface. J. Hydaul. Engng ASLE 116, 835–847.CrossRefGoogle Scholar
Kunugi, T. & Satake, S.-I. 2002 Direct numerical simulation of turbulent free surface flow with carbon dioxide gas absorption. Geophysical Monograph 127, Gas Transfer at Water Surfaces, pp. 77–82.Google Scholar
Lakehal, D., Fulgosi, M. & Yadigaroglu, G. 2003 Direct numerical simulation of turbulent heat transfer across a mobile, sheared gas–liquid interface. Trans. ASME: J. Heat Transfer 125, 1129–1139.CrossRefGoogle Scholar
Lamont, J. C. & Scott, D. S. 1970 An eddy cell model of mass transfer into the surface of a turbulent liquid. AIChE J. 16, 513–519.CrossRefGoogle Scholar
Lewis, W. K. & Whitman, W. G. 1924 Principles of gas absorption. Indust. Engng Chem. 16.CrossRefGoogle Scholar
McCready, M. J., Vassiliadou, E. & Hanratty, T. J. 1986 Computer-simulation of turbulent mass-transfer at a mobile interface. AIChE J. Chem. Engng Res. Dev. 32, 1108–1115.Google Scholar
McKenna, S. P. & McGillis, W. R. 2002 Surface divergence and air–water gas transfer. Geophysical Monograph 127, Gas Transfer at Water Surfaces, pp. 129–134.Google Scholar
McKenna, S. P. & McGillis, W. R. 2004 a Observations of flow repeatability and secondary circulation in oscillating grid-stirred tank. Phys. Fluids 16 (9), 3499–3502.CrossRefGoogle Scholar
McKenna, S. P. & McGillis, W. R. 2004 b The role of free-surface turbulence and surfactants in air–water gas transfer. Intl J. Heat Mass Transfer 47, 539–553.CrossRefGoogle Scholar
Magnaudet, J. & Calmet, I. 2006 Turbulent mass transfer through a flat shear-free surface. J. Fluid Mech. 553, 155–185.CrossRefGoogle Scholar
Matsunaga, N., Sugihara, Y., Komatsu, T. & Masuda, A. 1999 Quantitative properties of oscillating-grid turbulence in a homogeneous fluid. J. Fluid Dyn. Res. 25, 147–165.CrossRefGoogle Scholar
Moog, D. B. & Jirka, G. H. 2002 Air–water gas transfer in uniform flows with large gravel-bed roughness. Geophysical Monograph 127, Gas Transfer at Water Surfaces, pp. 371–376.Google Scholar
Münsterer, T., Mayer, H. J. & JÄHne, B. 1995 Dual-tracer measurements of concentration profiles in the aqueous mass boundary layer. Air–Water Gas Transfer : 3rd Intl Symp. on Air–Water Gas Transfer, pp. 637–648.Google Scholar
O'Connor, D. J. & Dobbins, W. E. 1956 The mechanism of reaeration in natural streams. J. Sanitary Engng 82 (SA6), 1115–1140.Google Scholar
Pan, Y. & Banerjee, S. 1995 A numerical study of free surface turbulence in channel flow. Phys. Fluids 7, 1649–1664.CrossRefGoogle Scholar
Plate, E. J. & Friedrich, R. 1984 Reaeration of open channel flow. Gas Transfer at Air–Water Interfaces, pp. 333–346.Google Scholar
Prinos, P., Atmane, M. & George, J. 1995 Gas flux measurements and modelling below an air–water interface. Proc. 3rd Intl Symp. Air–Water Gas Transfer, pp. 49–57.Google Scholar
Roy, A. G., Buffin-Bélanger, T., Lamarre, H. & Kirkbride, A. D. 2004 Size, shape and dynamics of large-scale turbulent flow structures in a gravel-bed river. J. Fluid Mech. 500, 1–27.CrossRefGoogle Scholar
Sugihara, Y. & Tsumori, H. 2005 Surface-renewal eddies at the air–water interface in oscillating-grid turbulence. In Enviromental Hydraulics and Sustainable Water Management (ed. Lee, J. H. W. & Lam, K. M.), pp. 199–205.Google Scholar
Tamburrino, A. & Gulliver, J. S. 2002 Free-surface turbulence and mass transfer in a channel flow. AIChE J. 48, 2732–2743.CrossRefGoogle Scholar
Thackston, E. L. & Krenkel, P. A. 1969 Reaeration prediction in natural streams. J. Sanitary Engng Div. Proc. ASCE 95 (SA1), 65–93.CrossRefGoogle Scholar
Theofanus, T. G. 1984 Conceptual models of gas exchange. Gas Transfer at Air–Water Surfaces, pp. 271–281. Reidel.CrossRefGoogle Scholar
Theofanus, T. G., Houze, R. N. & Brumfield, L. K. 1976 Turbulent mass transfer at free, gas liquid interfaces with applications to open channel, bubble and jet flows. Intl J. Heat Mass Transfer 19.Google Scholar
Thompson, S. M. & Turner, J. S. 1975 Mixing across an interface due to turbulence generated by an oscillating grid. J. Fluid Mech. 67, 349–368.CrossRefGoogle Scholar
Turney, D. E., Smith, W. C. & Banerjee, S. 2005 A measure of near-surface fluid motions that predicts air–water gas transfer in a wide range of conditions. Geophys. Res. Lett. 32 (4).CrossRefGoogle Scholar
Vaughan, W. M. & Weber, G. 1970 Oxygen quenching of pyrenebutyric acid fluorescence in water, a dynamic probe of the microenvironment. Biochemistry 9, 464–473.CrossRefGoogle Scholar
Wolff, L. M. & Hanratty, T. J. 1994 Instantaneous concentration profiles of oxygen accompanying absorption in a stratified flow. Exps Fluids 16, 385–392.CrossRefGoogle Scholar
Woodrow, P. T. & Duke, S. R. 2002 LIF measurements of oxygen concentration gradients along flat and wavy air–water interfaces. Geophysical Monograph 127, Gas Transfer at Water Surfaces, pp. 83–88.Google Scholar