Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T00:33:53.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study on bubble dynamics subject to buoyancy

Published online by Cambridge University Press:  06 July 2015

A. M. Zhang ,
P. Cui ,
J. Cui  and
Q. X. Wang
A. M. Zhang*
Affiliation:
College of Shipbuilding Engineering, Harbin Engineering University, 145 Nantong Street, Harbin 150001, China
P. Cui
Affiliation:
College of Shipbuilding Engineering, Harbin Engineering University, 145 Nantong Street, Harbin 150001, China
J. Cui
Affiliation:
School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, 2 Mengxi Street, Zhenjiang 212003, China
Q. X. Wang
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the dynamics of large bubbles subject to various strengths of buoyancy effects, which are associated with applications for underwater explosion. The bubble is produced by electric discharge in a low-pressure tank to enhance the buoyancy effects. Experiments are carried out for a bubble in an infinite field, below a free surface and above a rigid boundary. The effects of buoyancy are reflected by the dimensionless parameter 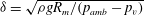${\it\delta}=\sqrt{{\it\rho}gR_{m}/(p_{amb}-p_{v})}$, where 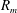$R_{m}$, 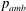$p_{amb}$, 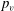$p_{v}$, 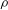${\it\rho}$ and 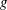$g$ are the maximum bubble radius, ambient pressure, saturated vapour pressure, density of water and the acceleration of gravity respectively. A systematic study of buoyancy effects is carried out for a wide range of 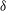${\it\delta}$ from 0.034 to 0.95. A series of new phenomena and new features is observed. The bubbles recorded are transparent, and thus we are able to display and study the jet formation, development and impact on the opposite bubble surface as well as the subsequent collapsing and rebounding of the ring bubble. Qualitative analyses are carried out for the bubble migration, jet velocity and jet initiation time, etc. for different values of 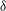${\it\delta}$. When a bubble oscillates below a free surface or above a rigid boundary, the Bjerknes force due to the free surface (or rigid boundary) and the buoyancy are in opposite directions. Three situations are studied for each of the two configurations: (i) the Bjerknes force being dominant, (ii) the buoyancy force being dominant and (iii) the two forces being approximately balanced. For case (iii), we further consider two subcases, where both the balanced Bjerknes and buoyancy forces are weak or strong. When the Bjerknes and buoyancy forces are approximately balanced over the pulsation, some representative bubble behaviours are observed: the bubble near free surface is found to split into two parts jetting away from each other for small 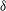${\it\delta}$, or involutes from both top and bottom for large 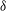${\it\delta}$. A bubble above a rigid wall is found to be subject to contraction from the lateral part leading to bubble splitting. New criteria are established based on experimental results for neutral collapses where there is no dominant jetting along one direction, which correlate well with the criteria of Blake et al. (J. Fluid Mech., vol. 170, 1986, pp. 479–497; J. Fluid Mech., vol. 181, 1987, pp. 197–212) but agree better with the experimental and computational results.

JFM classification

Drops and Bubbles: Bubble dynamics Drops and Bubbles: Cavitation Drops and Bubbles: Drops and Bubbles
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 137 - 160
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhatov, I., Lindau, O., Topolnikov, A., Mettin, R., Vakhitova, N. & Lauterborn, W. 2001 Collapse and rebound of a laser-induced cavitation bubble. Phys. Fluids 13, 2805–2819.Google Scholar
Benjamin, T. & Ellis, A. T. 1966 The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries. Phil. Trans. R. Soc. Lond. A 260, 221–240.Google Scholar
Best, J. P. & Kucera, A. 1992 A numerical investigation of non-spherical rebounding bubbles. J. Fluid Mech. 245, 137–154.Google Scholar
Best, J. P., Soh, W. K. & Yu, C. F. 1996 An experimental investigation of buoyant transient cavity collapse near rigid cylindrical boundaries. Trans. ASME J. Fluids Engng 118, 195–198.CrossRefGoogle Scholar
Blake, J. R. & Gibson, D. C. 1981 Growth and collapse of a vapour cavity near a free surface. J. Fluid Mech. 111, 123–140.Google Scholar
Blake, J. R. & Gibson, D. C. 1987 Cavitation bubbles near boundaries. Annu. Rev. Fluid Mech. 19, 99–123.Google Scholar
Blake, J. R., Taib, B. B. & Doherty, G. 1986 Transient cavities near boundaries. Part 1. Rigid boundary. J. Fluid Mech. 170, 479–497.Google Scholar
Blake, J. R., Taib, B. B. & Doherty, G. 1987 Transient cavities near boundaries. Part 2. Free surface. J. Fluid Mech. 181, 197–212.Google Scholar
Boulton-Stone, J. M. & Blake, J. R. 1993 Gas bubbles bursting at a free surface. J. Fluid Mech. 254, 437–466.CrossRefGoogle Scholar
Brett, J. M. & Yiannakopolous, G. 2008 A study of explosive effects in close proximity to a submerged cylinder. Intl J. Impact Engng 35, 206–225.Google Scholar
Brett, J. M., Yiannakopoulos, G. & van der Schaaf, P. J. 2000 Time-resolved measurement of the deformation of submerged cylinders subjected to loading from a nearby explosion. Intl J. Impact Engng 24, 875–890.CrossRefGoogle Scholar
Brujan, E. A., Keen, G. S., Vogel, A. & Blake, J. R. 2002 The final stage of the collapse of a cavitation bubble close to a rigid boundary. Phys. Fluids 14, 85–92.Google Scholar
Brujan, E. A., Nahen, K., Schmidt, P. & Vogel, A. 2001 Dynamics of laser-induced cavitation bubbles near an elastic boundary. J. Fluid Mech. 433, 251–281.Google Scholar
Brujan, E. A., Pearson, A. & Blake, J. R. 2005 Pulsating, buoyant bubbles close to a rigid boundary and near the null final Kelvin impulse state. Intl J. Multiphase Flow 31, 302–317.Google Scholar
Buogo, S. & Cannelli, G. B. 2002 Implosion of an underwater spark-generated bubble and acoustic energy evaluation using the Rayleigh model. J. Acoust. Soc. Am. 111, 2594–2600.Google Scholar
Chahine, G. L. 1977 Interaction between an oscillating bubble and a free surface. Trans. ASME J. Fluids Engng 99, 709–716.Google Scholar
Chahine, G. L.1997 Numerical and experimental study of explosion bubble crown jetting behavior. Dynaflow, Inc. Tech. Rep. 96003-1.Google Scholar
Chahine, G. & Bovis, A. 1980 Oscillation and collapse of a cavitation bubble in the vicinity of a two-liquid interface. In Cavitation and Inhomogeneities in Underwater Acoustics (ed. Lauterborn, W.), pp. 23–29. Springer.CrossRefGoogle Scholar
Chahine, G., Frederick, G., Lambrecht, C., Harris, G. & Mair, H.1995 Spark-generated bubbles as laboratory-scale models of underwater explosions and their use for validation of simulation tools. In Proceedings of the 66th Shock and Vibration Symposium, vol. 2, pp. 265–277. SAVIAC, Shock & Vibration Information Analysis Center.Google Scholar
Cole, R. H. 1948 Underwater Explosions. Princeton University Press.CrossRefGoogle Scholar
Dadvand, A., Khoo, B. C. & Shervani-Tabar, M. T. 2009 A collapsing bubble-induced microinjector: an experimental study. Exp. Fluids 46, 419–434.CrossRefGoogle Scholar
Gibson, D. C. 1972 The kinetic and thermal expansion of vapor bubbles. Trans. ASME J. Fluids Engng 94, 89–95.CrossRefGoogle Scholar
Gibson, D. C. & Blake, J. R. 1982 The growth and collapse of bubbles near deformable surfaces. Appl. Sci. Res. 38, 215–224.CrossRefGoogle Scholar
Gonzalez-Avila, S. R., Klaseboer, E., Khoo, B. C. & Ohl, C. 2011 Cavitation bubble dynamics in a liquid gap of variable height. J. Fluid Mech. 682, 241–260.Google Scholar
Harvey, S. B., Best, J. P. & Soh, W. K. 1996 Vapour Bubble Measurement Using Image Analysis. Institute of Physics Publishing.Google Scholar
Hooton, M. C., Blake, J. R. & Soh, W. K. 1994 Behaviour of an underwater explosion bubble near a rigid boundary: theory and experiment. In Bubble Dynamics and Interface Phenomena (ed. Blake, J. R., Boulton-Stone, J. M. & Thomas, N. H.), pp. 421–428. Springer.CrossRefGoogle Scholar
Hung, C. & Hwangfu, J. 2010 Experimental study of the behaviour of mini-charge underwater explosion bubbles near different boundaries. J. Fluid Mech. 651, 55–80.Google Scholar
Jayaprakash, A., Hsiao, C.-T. & Chahine, G. 2012 Numerical and experimental study of the interaction of a spark-generated bubble and a vertical wall. Trans. ASME J. Fluids Engng 134, 031301.Google Scholar
Jin, Y. H., Shaw, S. J. & Emmony, D. C. 1996 Observations of a cavitation bubble interacting with a solid boundary as seen from below. Phys. Fluids 8, 1699–1701.Google Scholar
Kan, K. K., Stuhmiller, J. H. & Chan, P. C. 2005 Simulation of the collapse of an underwater explosion bubble under a circular plate. Shock Vib. 12, 217–225.CrossRefGoogle Scholar
Klaseboer, E., Hung, K. C., Wang, C., Wang, C. W., Khoo, B. C., Boyce, P., Debono, S. & Charlier, H. 2005 Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure. J. Fluid Mech. 537, 387–413.Google Scholar
Krieger, J. R. & Chahine, G. L.2003 Dynamics and acoustic signature of non-spherical underwater explosion bubbles. In Proceedings of 74th Shock and Vibration Symposium. CD Edition.Google Scholar
Krieger, J. R. & Chahine, G. L. 2005 Acoustic signals of underwater explosions near surfaces. J. Acoust. Soc. Am. 118, 2961–2974.Google Scholar
Lauterborn, W. 1982 Cavitation bubble dynamics – new tools for an intricate problem. Appl. Sci. Res. 38, 165–178.Google Scholar
Lauterborn, W. & Bolle, H. 1975 Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary. J. Fluid Mech. 72, 391–399.Google Scholar
Lauterborn, W. & Hentschel, W. 1985 Cavitation bubble dynamics studied by high speed photography and holography: part one. Ultrasonics 23, 260–268.CrossRefGoogle Scholar
Lauterborn, W. & Vogel, A. 1984 Modern optical techniques in fluid mechanics. Annu. Rev. Fluid Mech. 16, 223–244.Google Scholar
Lindau, O. & Lauterborn, W. 2003 Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J. Fluid Mech. 479, 327–348.Google Scholar
Obreschkow, D., Kobel, P., Dorsaz, N., De Bosset, A., Nicollier, C. & Farhat, M. 2006 Cavitation bubble dynamics inside liquid drops in microgravity. Phys. Rev. Lett. 97, 094502.Google Scholar
Obreschkow, D., Tinguely, M., Dorsaz, N., Kobel, P., De Bosset, A. & Farhat, M. 2011 Universal scaling law for jets of collapsing bubbles. Phys. Rev. Lett. 107, 204501.Google Scholar
Ohl, C. D., Philipp, A. & Lauterborn, W. 1995 Cavitation bubble collapse studied at 20 million frames per second. Ann. Phys. 4, 26–34.Google Scholar
Pearson, A., Cox, E., Blake, J. R. & Otto, S. R. 2004 Bubble interactions near a free surface. Engng Anal. Bound. Elem. 28, 295–313.CrossRefGoogle Scholar
Philipp, A. & Lauterborn, W. 1998 Cavitation erosion by single laser-produced bubbles. J. Fluid Mech. 361, 75–116.Google Scholar
Robinson, P. B., Blake, J. R., Kodama, T., Shima, A. & Tomita, Y. 2001 Interaction of cavitation bubbles with a free surface. J. Appl. Phys. 89, 8225–8237.Google Scholar
Shaw, S. J., Jin, Y. H., Gentry, T. P. & Emmony, D. C. 1999 Experimental observations of the interaction of a laser generated cavitation bubble with a flexible membrane. Phys. Fluids 11, 2437–2439.CrossRefGoogle Scholar
Shaw, S. J., Jin, Y. H., Schiffers, W. P. & Emmony, D. C. 1996 The interaction of a laser-generated cavity in water with a solid surface. J. Acoust. Soc. Am. 99, 2811–2824.Google Scholar
Shima, A. & Nakajima, K. 1977 Collapse of a non-hemispherical bubble attached to a solid wall. J. Fluid Mech. 80, 369–391.Google Scholar
Shima, A., Takayama, K. & Tomita, Y. 1983 Mechanism of impact pressure generation from spark-generated bubble collapse near a wall. AAIA J. 21, 55–59.CrossRefGoogle Scholar
Shima, A., Tomita, Y., Gibson, D. C. & Blake, J. R. 1989 The growth and collapse of cavitation bubbles near composite surfaces. J. Fluid Mech. 203, 199–214.Google Scholar
Snay, H. G.1962a Underwater explosion phenomena: the parameters of migrating bubbles. NAVORD Report 4135.CrossRefGoogle Scholar
Snay, H. G.1962b Charts for the parameters of migrating explosion bubbles. NOLTR Report 62–184.Google Scholar
Tomita, Y. & Kodama, T. 2003 Interaction of laser-induced cavitation bubbles with composite surfaces. J. Appl. Phys. 94, 2809–2816.Google Scholar
Tomita, Y. & Shima, A. 1986 Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse. J. Fluid Mech. 169, 535–564.Google Scholar
Tong, R. P., Schiffers, W. P., Shaw, S. J., Blake, J. R. & Emmony, D. C. 1999 The role of ‘splashing’ in the collapse of a laser-generated cavity near a rigid boundary. J. Fluid Mech. 380, 339–361.CrossRefGoogle Scholar
Turangan, C. K., Ong, G. P., Klaseboer, E. & Khoo, B. C. 2006 Experimental and numerical study of transient bubble–elastic membrane interaction. J. Appl. Phys. 100, 054910.CrossRefGoogle Scholar
Vogel, A., Lauterborn, W. & Timm, R. 1989 Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary. J. Fluid Mech. 206, 299–338.Google Scholar
Wang, Q. X. 1998 The evolution of a gas bubble near an inclined wall. J. Theor. Comput. Fluid Dyn. 12, 29–51.Google Scholar
Wang, Q. X. 2004 Numerical simulation of violent bubble motion. Phys. Fluids 16, 1610–1619.Google Scholar
Wang, Q. X. 2013 Underwater explosion bubble dynamics in a compressible liquid. Phys. Fluids 25, 072104.Google Scholar
Wang, Q. X., Yeo, K. S., Khoo, B. C. & Lam, K. Y. 1996a Nonlinear interaction between gas bubble and free surface. Comput. Fluids 25, 607–628.CrossRefGoogle Scholar
Wang, Q. X., Yeo, K. S., Khoo, B. C. & Lam, K. Y. 1996b Strong interaction between a buoyancy bubble and a free surface. Theor. Comput. Fluid Dyn. 8, 73–88.Google Scholar
Yang, Y. X., Wang, Q. X. & Tan, S. K. 2013 Dynamic features of a laser-induced cavitation bubble near a solid boundary. Ultrason. Sonochem. 20, 1098–1103.Google Scholar
Zhang, A. M. & Liu, Y. L. 2015 Improved three-dimensional bubble dynamics model based on boundary element method. J. Comput. Phys. 294, 208–223.Google Scholar
Zhang, A. M., Wang, S. P., Huang, C. & Wang, B 2013 Influences of initial and boundary conditions on underwater explosion bubble dynamics. Eur. J. Mech. (B/Fluids) 42, 69–91.Google Scholar