Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-26T02:52:26.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study of the influence of anisotropy on the inertial scales of turbulence

Published online by Cambridge University Press:  09 January 2012

Kelken Chang ,
Gregory P. Bewley  and
Eberhard Bodenschatz
Kelken Chang
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany International Collaboration for Turbulence Research
Gregory P. Bewley*
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany International Collaboration for Turbulence Research
Eberhard Bodenschatz
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany International Collaboration for Turbulence Research
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We ask whether the scaling exponents or the Kolmogorov constants depend on the anisotropy of the velocity fluctuations in a turbulent flow with no shear. According to our experiment, the answer is no for the Eulerian second-order transverse velocity structure function. The experiment consisted of 32 loudspeaker-driven jets pointed toward the centre of a spherical chamber. We generated anisotropy by controlling the strengths of the jets. We found that the form of the anisotropy of the velocity fluctuations was the same as that in the strength of the jets. We then varied the anisotropy, as measured by the ratio of axial to radial root-mean-square (r.m.s.) velocity fluctuations, between 0.6 and 2.3. The Reynolds number was approximately constant at around . 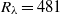In a central volume with a radius of 50 mm, the turbulence was approximately homogeneous, axisymmetric, and had no shear and no mean flow. We observed that the scaling exponent of the structure function was 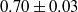, independent of the anisotropy and regardless of the direction in which we measured it. The Kolmogorov constant, 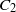, was also independent of direction and anisotropy to within the experimental error of 4 %.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 692 , 10 February 2012 , pp. 464 - 481
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Albrecht, H.-E., Borys, M., Damaschke, N. & Tropea, C. 2003 Laser Doppler and Phase Doppler Measurement Techniques. Springer.Google Scholar
2.Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
3.Benzi, R., Ciliberto, S., Baudet, C. & Chavarria, G. R. 1995 On the scaling of three-dimensional homogeneous and isotropic turbulence. Physica D 80, 385–398.CrossRefGoogle Scholar
4.Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E 48, R29–R32.Google Scholar
5.Bewley, G. P., Sreenivasan, K. R. & Lathrop, D. P. 2008 Particles for tracing turbulent liquid helium. Exp. Fluids 44, 887–896.Google Scholar
6.Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414, 43–164.Google Scholar
7.Buchhave, P. 1975 Biasing errors in individual particle measurements. In LDA Symposium of Copenhagen, Tonsbakken 16–18, 2740 Skovlunde, Denmark, pp. 258–278.Google Scholar
8.Buchhave, P., George, W. K. Jr & Lumley, J. L. 1979 The measurement of turbulence with the laser-Doppler anemometer. Annu. Rev. Fluid Mech. 11, 443–504.Google Scholar
9.Buša, J., Hnatich, M., Honkonen, J. & Horvath, D. 1997 Stability of Kolmogorov scaling in anisotropically forced turbulence. Phys. Rev. E 55, 381–394.Google Scholar
10.Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.Google Scholar
11.Fox, R. F., Gatland, I. R., Roy, R. & Vemuri, G. 1988 Fast, accurate algorithm for numerical simulation of exponentially correlated coloured noise. Phys. Rev. A 38, 5938–5940.Google Scholar
12.Glezer, A. & Amitay, M. 2002 Synthetic jets. Annu. Rev. Fluid Mech. 34, 503–529.Google Scholar
13.Goepfert, C., Marié, J.-L., Chareyron, D. & Lance, M. 2010 Characterization of a system generating a homogeneous isotropic turbulence field by free synthetic jets. Exp. Fluids 48, 809–822.Google Scholar
14.Hussein, H. J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.Google Scholar
15.Hwang, W. & Eaton, J. K. 2004 Creating homogeneous and isotropic turbulence without a mean flow. Exp. Fluids 36, 444–454.Google Scholar
16.Kolmogorov, A. N. 1941 Local structure of turbulence in an incompressible fluid at very high Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
17.Kurien, S. & Sreenivasan, K. R. 2001 Measures of anisotropy and the universal properties of turbulence. In New Trends in Turbulence (Turbulence: Nouveaux Aspects), Les Houches Session LXXIV, pp. 53–111. Springer.Google Scholar
18.Lu, J., Fugal, J. P., Nordsiek, H., Saw, E. W., Shaw, R. A. & Yang, W. 2008 Lagrangian particle tracking in three dimensions via single-camera in-line digital holography. New J. Phys. 10, 125013.Google Scholar
19.Ouellette, N. T., Xu, H., Bourgoin, M. & Bodenschatz, E. 2006 Small-scale anisotropy in Lagrangian turbulence. New J. Phys. 8, 102.Google Scholar
20.Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
21.Shen, X. & Warhaft, Z. 2002 Longitudinal and transverse structure functions in sheared and unsheared wind-tunnel turbulence. Phys. Fluids 14, 370–381.Google Scholar
22.Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.Google Scholar
23.Staicu, A., Vorselaars, B. & van de Water, W. 2003 Turbulence anisotropy and the SO(3) description. Phys. Rev. E 68, 046303.Google Scholar
24.Tavoularis, S. & Corrsin, S. 1981 Experiments in nearly homogeneous turbulent shear flow with uniform mean temperature gradient. Part 1. J. Fluid Mech. 104, 311–347.Google Scholar
25.Voth, G. A., La Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.Google Scholar
26.Warnaars, T. A., Hondzo, M. & Carper, M. A. 2006 A desktop apparatus for studying interactions between microorganisms and small-scale fluid motion. Hydrobiologia 563, 431–443.Google Scholar
27.Webster, D. R., Brathwaite, A. & Yen, J. 2004 A novel laboratory apparatus for simulating isotropic oceanic turbulence at low Reynolds number. Limnol. Oceanogr. Methods 2, 1–12.Google Scholar
28.Yeung, P. K. & Brasseur, J. G. 1991 The response of isotropic turbulence to isotropic and anisotropic forcing at the large scales. Phys. Fluids A 3, 884–897.Google Scholar
29.Zimmermann, R., Xu, H., Gasteuil, Y., Bourgoin, M., Volk, R., Pinton, J.-F. & Bodenschatz, E. 2010 The Lagrangian exploration module: an apparatus for the study of statistically homogeneous and isotropic turbulence. Rev. Sci. Instrum. 81, 055112.CrossRefGoogle Scholar